Newton's Second Law of Motion
Student Extras
Improve your problem-solving skills with problems, answers and solutions from The Calculator Pad.
Skateboard Science
Learn about the physics of skateboarding from the Exploratorium Museum website.
The Science of Speed
Learn about NASCAR racing at the National Science Foundation's Science of Speed website.
Lunar Lander GameLearn physics and have phun with PhET's Lunar Lander game.
PhET Simulation: Forces in 1 Dimension
Explore the relationship between individual forces, the net force and the resulting motion with this PhET simulation.
Flickr PhysicsVisit The Physics Classroom's Flickr Galleries and take a visual overview of Newton's laws of motion.
Physics of Baseball BatsThis page combines two of America's favorite pastimes - baseball (the forces between bat and ball) and physics.
Teacher's Guide
Thinking Physics! Present your students with this short decision-making challenge.
PhET Simulation: Forces in 1 Dimension
Allow students to explore the relationship between individual forces, the net force and the resulting acceleration with this PHET simulation.
Problem Based Learning: Measuring the Mass of a Car
This problem-based learning unit offers an alternative approach to introducing Newton's second law.
The LaboratoryLooking for a lab that coordinates with this page? Try the F-m-a Lab from The Laboratory. Requires motion detectors.
Treasures from TPFNeed ideas? Need help? Explore The Physics Front's treasure box of catalogued resources on Newton's second law.
Curriculum CornerLearning requires action. Give your students this sense-making activity from The Curriculum Corner.
PBS TeachersView a lesson plan from PBS Teachers on the topic of Newton's Laws.
Newton's Second Law
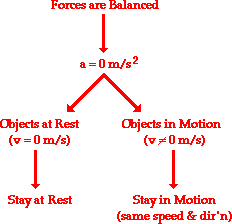
Newton's first law of motion predicts the behavior of objects for which all existing forces are balanced. The first law - sometimes referred to as the law of inertia - states that if the forces acting upon an object are balanced, then the acceleration of that object will be 0 m/s/s. Objects at equilibrium (the condition in which all forces balance) will not accelerate. According to Newton, an object will only accelerate if there is a net or unbalanced force acting upon it. The presence of an unbalanced force will accelerate an object - changing its speed, its direction, or both its speed and direction.
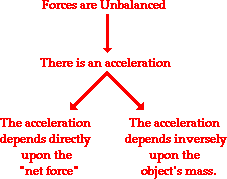
Newton's second law of motion pertains to the behavior of objects for which all existing forces are not balanced. The second law states that the acceleration of an object is dependent upon two variables - the net force acting upon the object and the mass of the object. The acceleration of an object depends directly upon the net force acting upon the object, and inversely upon the mass of the object. As the force acting upon an object is increased, the acceleration of the object is increased. As the mass of an object is increased, the acceleration of the object is decreased.
Newton's second law of motion can be formally stated as follows:
The acceleration of an object as produced by a net force is directly proportional to the magnitude of the net force, in the same direction as the net force, and inversely proportional to the mass of the object.
This verbal statement can be expressed in equation form as follows:
a = Fnet /
m
The above equation is often rearranged to a more familiar form as shown below. The net force is equated to the product of the mass times the acceleration.
Fnet = m *
a
In
this entire discussion, the emphasis has been on the net
force. The acceleration is directly proportional to the
net force; the net force equals mass times
acceleration; the acceleration in the same direction as the
net force; an acceleration is produced by a net
force. The NET FORCE. It is important to remember this
distinction. Do not use the value of merely "any 'ole force"
in the above equation. It is the net force that is related
to acceleration. As discussed in an
earlier lesson, the net force is the vector sum of all
the forces. If all the individual forces acting upon an
object are known, then the net force can be determined. If
necessary, review this principle by returning to the
practice questions in Lesson
2.
Consistent with the above equation, a unit of force is equal to a unit of mass times a unit of acceleration. By substituting standard metric units for force, mass, and acceleration into the above equation, the following unit equivalency can be written.
The definition of the standard metric unit of force is stated by the above equation. One Newton is defined as the amount of force required to give a 1-kg mass an acceleration of 1 m/s/s.
The
Fnet = m • a equation is often used in
algebraic problem solving. The table below can be filled by
substituting into the equation and solving for the unknown
quantity. Try it yourself and then use the click on the
buttons to view the answers.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
The numerical information in the table above demonstrates some important qualitative relationships between force, mass, and acceleration. Comparing the values in rows 1 and 2, it can be seen that a doubling of the net force results in a doubling of the acceleration (if mass is held constant). Similarly, comparing the values in rows 2 and 4 demonstrates that a halving of the net force results in a halving of the acceleration (if mass is held constant). Acceleration is directly proportional to net force.
Furthermore, the qualitative relationship between mass and acceleration can be seen by a comparison of the numerical values in the above table. Observe from rows 2 and 3 that a doubling of the mass results in a halving of the acceleration (if force is held constant). And similarly, rows 4 and 5 show that a halving of the mass results in a doubling of the acceleration (if force is held constant). Acceleration is inversely proportional to mass.
The analysis of the table data illustrates that an equation such as Fnet = m*a can be a guide to thinking about how a variation in one quantity might effect another quantity. Whatever alteration is made of the net force, the same change will occur with the acceleration. Double, triple or quadruple the net force, and the acceleration will do the same. On the other hand, whatever alteration is made of the mass, the opposite or inverse change will occur with the acceleration. Double, triple or quadruple the mass, and the acceleration will be one-half, one-third or one-fourth its original value.
As
stated above, the direction of the net force is in the
same direction as the acceleration. Thus, if the direction
of the acceleration is known, then the direction of the net
force is also known. Consider the two oil
drop diagrams below for an acceleration of a car. From
the diagram, determine the direction of the net force that
is acting upon the car. Then click the buttons to view the
answers. (If necessary,
review acceleration from the previous unit.)
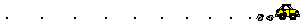
In conclusion, Newton's second law provides the explanation for the behavior of objects upon which the forces do not balance. The law states that unbalanced forces cause objects to accelerate with an acceleration that is directly proportional to the net force and inversely proportional to the mass.
Rocket Science!
Check
Your Understanding
1. Determine the accelerations that result when a 12-N net force is applied to a 3-kg object and then to a 6-kg object.
2. A net force of 15 N is exerted on an encyclopedia to cause it to accelerate at a rate of 5 m/s2. Determine the mass of the encyclopedia.
3. Suppose that a sled is accelerating at a rate of 2 m/s2. If the net force is tripled and the mass is doubled, then what is the new acceleration of the sled?
4. Suppose that a sled is accelerating at a rate of 2 m/s2. If the net force is tripled and the mass is halved, then what is the new acceleration of the sled?