Maximum Range
Imagine a cannonball launched from a cannon at three different launch angles - 30-degrees, 45-degrees, and 60-degrees. The launch speed is held constant; only the angle is changed. Imagine as well that the cannonballs do not encounter a significant amount of air resistance. How will the trajectories of the three cannonballs compare? Which cannonball will have the greatest range? Which cannonball will reach the highest peak height before falling? Which cannonball will reach the ground first? The animation below depicts such a situation. The path of the cannonballs are shown. Additionally, the velocity components (horizontal and vertical) are represented by arrows in the animation.
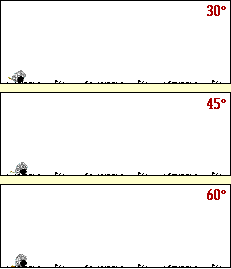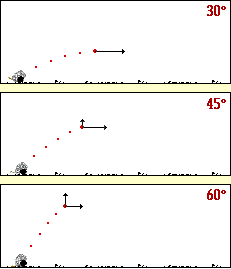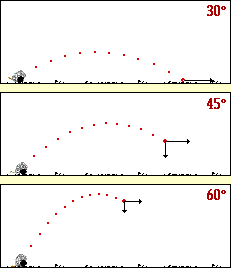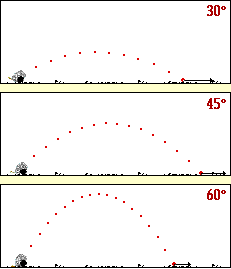
As can be seen from the above animation, each cannonball follows a parabolic path. The cannonball launched at a 45-degree angle had the greatest range. The cannonball launched at a 60-degree angle had the highest peak height before falling. The cannonball launched at the 30-degree angle reached the ground first.
An analysis of the velocity components for these three projectiles reveals reasons for these observations. The peak height of a projectile is determined by the initial value of the vertical velocity component. The greater the initial value of vy, the higher that a projectile will rise. The projectile launched at 60-degrees has the greatest vy, and as such the greatest peak height. The "hang time" of a projectile is also determined by the initial value of the vertical velocity component. The smaller the initial value of vy, the shorter the hang time. The projectile launched at 30-degrees has the smallest vy, and as such the shortest hang time. The range of a projectile is determined by two parameters - the initial value of the horizontal velocity component and the hang time of the projectile. As can be seen from the animation, the projectile launched at 60-degrees has the greatest hang time; yet its range is limited by the fact that the vx is the smallest of all three angles. The projectile launched at 30-degrees has the greatest vx of all three launch angles; yet its range is limited by the fact that the hang time is so short. The projectile launched at 45-degree does not win in either category, yet the fact that it is able to place a strong showing in each category contributes to its ability to achieve the greatest range. More sophisticated arguments for why the 45-degree launch angle yields the greatest range exist; yet since they involve the use of calculus, they are not presented here.
For more information on physical descriptions of motion, visit The Physics Classroom Tutorial. Detailed information is available there on the following topics:
Projectiles
Characteristics of a Projectile's Trajectory
Describing Projectiles with Numbers
Initial Velocity Components