Circular Motion and Gravitation Review
Navigate to:
Review Session Home - Topic Listing
Circular Motion and Gravitation - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-14 || #15-28 || #29-40
Part C: Diagramming and Analysis
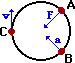 15. In the diagram at the right, draw vector arrows (straight lines with arrowheads) which indicate the following for an object which is moving in a clockwise circle.
15. In the diagram at the right, draw vector arrows (straight lines with arrowheads) which indicate the following for an object which is moving in a clockwise circle.
- the net force at point A.
- the acceleration at point B.
- the velocity at point C.
|
Answer:
See diagram for answers. The force and acceleration vectors are directed inwards towards the center of the circle and the velocity vector is directed tangent to the circle.
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
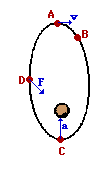 16. The diagram at the right shows a satellite orbiting the Earth in an elliptical path in a clockwise direction.
16. The diagram at the right shows a satellite orbiting the Earth in an elliptical path in a clockwise direction.
- Draw a vector representing the velocity of the object at position A.
- raw a vector representing the force on the object at position D.
- Draw a vector representing the acceleration of the object at position C.
- At which of the four positions is the satellite moving fastest?
|
Answer:
See diagram for answers. The force and acceleration vectors are directed towards the planet being orbited (which is at a foci of the ellipse) and the velocity vector is directed tangent to the path.
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
17. A 1.20-kg bucket is held by a string and whirled in a vertical circle. The radius of the circle is 1.30 m. The speed of the bucket is 3.70 m/s at the top of the loop and 7.10 m/s at the bottom of the loop. On the diagrams below, construct a free-body diagram (label all forces according to type) for the bucket at both the top and the bottom of the loop. Fill in the blanks and clearly indicate the magnitude of the individual force values on your free-body diagram.
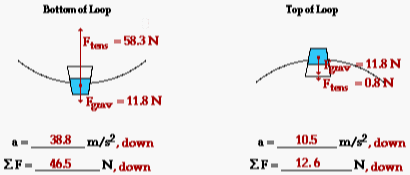
|
Answers: See diagram above.
In each case, the acceleration is found using the equation: a = v2/R. For the top of the loop, a = (3.70)2/(1.30) = 10.53 m/s2. For the bottom of the loop, a = (7.10)2/(1.30) = 38.78 m/s2. The net force is always found by Fnet = m•a. At the bottom of the loop, Fnet = (1.20 kg)•(10.53 m/s2) = 12.6 N. At the bottom of the loop, Fnet = (1.20 kg)•(38.78 m/s2) = 46.5 N. The force of gravity is always found by m•g where g = 9.8 m/s2. At both top and bottom of the loop, this value is 11.8 N. From the free-body diagram, one can reason the following:
Top: Fnet = Fgrav + Ftens which can be rearranged to Ftens = Fnet - Fgrav
Bottom: Fnet = Ftens - Fgrav which can be rearranged to Ftens = Fnet + Fgrav
Using these equations and the calculated values of Fgrav and Fnet, one can determine the tension at the top and bottom of the circle.
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
18. Construct a free-body diagram showing the direction and types of forces acting upon the car at the top and the bottom of a loop. Be sure to label the forces according to type.

Anna experiences a downward acceleration of 24.0 m/s2 at the top of the loop and an upwards acceleration of 12.0 m/s2 at the bottom of the loop. Use Newton's second law to fill in all the blanks and to ultimately determine the normal force acting upon Anna's 800. kg roller coaster car. PSYW
|
Top
|
Bottom
|
|
Fnet = 19200 N, down
|
Fnet = 9600 N, up
|
|
Fgrav = 7840 N, down
|
Fgrav = 7840 N, down
|
|
Fnorm = 11360 N, down
|
Fnorm = 17440 N, up
|
|
Answer: See diagram and table above.
This problem is very similar to question #17 above. The net force is found by calculating m•a; its direction is in the same direction as the a vector. The gravitational force is found from m•g; the value of 9.8 m/s/s is used for g. Now the free-body diagram can be used to generate the following equations for the top and the bottom of the loop:
Top: Fnet = Fgrav + Fnorm which can be rearranged to Fnorm = Fnet - Fgrav
Bottom: Fnet = Fnorm - Fgrav which can be rearranged to Fnorm = Fnet + Fgrav
The difference in these two equations is attributed to the fact that at the top of the loop, the Fnorm and the Fgrav point in the same direction as the net force vector; at the bottom of the loop, they point in opposite directions. Using the calculated values of Fnet and Fgrav, the normal force can now be calculated.
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
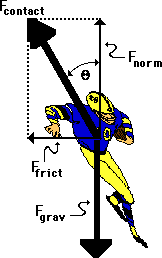 19. A fullback is running a sweep around the left side of the line. As he rounds the turn, he is momentarily moving in circular motion, sweeping out a quarter-circle with a radius of 4.17 meters. If the 83.5-kg fullback makes the turn with a speed of 5.21 m/s, then what is his acceleration, the net force, the angle of lean (measured to the vertical), and the total contact force with the ground? PSYW
19. A fullback is running a sweep around the left side of the line. As he rounds the turn, he is momentarily moving in circular motion, sweeping out a quarter-circle with a radius of 4.17 meters. If the 83.5-kg fullback makes the turn with a speed of 5.21 m/s, then what is his acceleration, the net force, the angle of lean (measured to the vertical), and the total contact force with the ground? PSYW
a = 6.51 m/s2
Fnet = 544 N
Fgrav = 818 N
Fnorm = 818 N
Ffrict = 544 N
Fcontact = 982 N
Angle of Lean = 33.6 degrees
|
Answer: See table above,
The acceleration is found using the equation: a = v2/R. For the top of the loop, a = (5.21)2/(4.17) = 6.51 m/s2. The net force is always found by Fnet = m•a. For the fullback, Fnet = (83.5 kg)•(6.51 m/s2) = 544 N. This net force is directed inwards and as such, it is equal to the force of friction supplied by the ground. Subsequently, Ffrict = 544 N. The force of gravity is always found by m•g where g = 9.8 m/s2. Using the fullback's mass, this value is 818 N. Since the normal force must support the fullback's weight, it is equal in magnitude to the force of gravity; so Fnorm = 818 N. The contact force is the resultant force of the Fnorm and Ffrict. Its value can be determined using the Pythagorean theorem: Fcontact = SQRT[(544 N)2 + (818 N)2] = 982 N. The angle of lean (theta in the diagram above) can be found using either the sine or the tangent function. From the diagram, it is seen that the sine(theta) = Ffrict /Fcontact. Thus, theta is equal to sin-1(Ffrict /Fcontact) = sin-1 (544 N/982 N) = 33.6 degrees.
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
 20. Pete Zaria is riding the Cliff Hanger at Great America. Pete enters a cylindrical barrel which makes 18.5 revolutions every minute. The diameter of the barrel is 6.92 m. Pete's mass is 64.7 kg. Construct a free-body diagram showing the forces acting upon Pete. Calculate the acceleration and net force acting upon Pete Zaria. Finally, determine the coefficient of friction between Pete and the walls that would be required to support Pete's weight. PSYW
20. Pete Zaria is riding the Cliff Hanger at Great America. Pete enters a cylindrical barrel which makes 18.5 revolutions every minute. The diameter of the barrel is 6.92 m. Pete's mass is 64.7 kg. Construct a free-body diagram showing the forces acting upon Pete. Calculate the acceleration and net force acting upon Pete Zaria. Finally, determine the coefficient of friction between Pete and the walls that would be required to support Pete's weight. PSYW
|
Answer: 0.755
As usual, Fgrav = m•g = (64.7 kg)•(9.8 m/s/s) = 634 N. This downward force must be balanced by the friction force since there is no vertical acceleration. Therefore, Ffrict = 634 N. The net inward force is supplied by the normal force; so a calculation of the net force will yield the value of the normal force. Acceleration is found from speed and radius. The speed is:
v = (18.5 rev/60 sec)• (2 • pi • 3.46 m/rev) = 6.703 m/s.
Now the acceleration is:
a = v2/R = (6.703 m/s)2/(3.46 m) = 12.986 m/s2
Now the net force (and the normal force) can be calculated:
Fnet = Fnorm = m•a = (64.7 kg)•(12.986 m/s/s) = 840.20 N
Now that the normal force and the friction force have been found, the coefficient of friction can be determined:
µ = (Ffrict)/(Fnorm) = (634 N)/(840.20 N) = 0.755
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
Part D: Short Computations
21. Two objects attract each other with a force of gravity (Fgrav) of 36 N. If the distance separating the objects is doubled, then what is the new force of gravitational attraction? PSYW
22. Two objects attract each other with a force of gravity (Fgrav) of 36 N. If the distance separating the objects is doubled and the masses one of the objects is tripled, then what is the new force of gravitational attraction? PSYW
23. Two objects attract each other with a force of gravity (Fgrav) of 36 N. If the distance separating the objects is increased by a factor of 4 and the masses of both objects are tripled, then what is the new force of gravitational attraction? PSYW
|
Answers:
For Questions #21-#23, Newton's universal gravitation equation must be used as a guide to thinking about how an alteration in one variable would effect another variable. From the equation, it can be deduced that a change in either one of the masses would produce a proportional change in the force of gravity. However, a change in the separation distance will produce the inverse square effect upon the force of gravity. So increasing separation distance by a factor of x, will decrease the force of gravity by a factor of x2. This reasoning leads to the following solutions.
21. New force = 36 N / 4 = 9.0 N
22. New force = 36 N • 3 / 4 = 27.0 N
23. New force = 36 N •3 •3 / 16 = 20.3 N
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
24. Suppose that the acceleration of gravity on the surface of planet X is 12 m/s/s. Determine the acceleration of gravity at a location ...
- of 2 radii from the center of planet X.
- of 4 radii from the center of planet X.
- of 2 radii from the surface of planet X.
- on the surface of planet X if the planet mass were twice as large (same radius).
- on the surface of planet X if the planet mass were one-half as large (same radius).
|
Answers:
Like the force of gravity, the acceleration of gravity varies inversely with distance. So increasing the separation distance by a factor of x, decreases the g value by a factor x2. An object on the surface of planet X is a distance of one-radius from its center. Success on this question depends on the ability to recognize from the given information the factor X by which the distance is changed (and in part e, the factor by which the mass is changed).
24a. g = (12 m/s/s) / 4 = 3 m/s/s
24b. g = (12 m/s/s) / 16 = 0.75 m/s/s
24c. g = (12 m/s/s) / 9 = 1.33 m/s/s (A distance of 2 radii from the surface is equivalent to 3 radii from the center of the planet.)
24d. g = (12 m/s/s)• 2 = 24 m/s/s
24e. g = (12 m/s/s) • 0.5 = 6 m/s/s
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
25. Suppose that a planet was located 12.0 times further from the sun than the earth's distance from the sun. Determine the period of the planet. PSYW
|
Answer: 41.6 yr
This question explores the R-T relationship. As such, Kepler's third law - that the T2/R3 ratio is the same for all the planets - must be utilized.
Tearth2/Rearth3 = Tplanet2/Rplanet3
(1 year)2/Rearth3 = Tplanet2 /(12.0•Rearth)3
Rearranging this equation to solve for the period of the planet yields the equation:
Tplanet2 = (1 year)2 • (12.0•Rearth)3 /Rearth3 = (1 year)2 • (12.0)3 = 1728 year2
Tplanet = SQRT(1728 year2 ) = 41.6 years
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
26. The acceleration of gravity on the moon is approximately one-sixth the value on earth's surface. If a person weighs 60.0 N on the moon's surface, what is his/her approximate mass on Earth? PSYW
|
Answer: 36.7 kg
If the g value on the moon is 1/6-th of the value of earth (gearth = 9.8 m/s2), then gmoon = 1.63 m/s/s. The mass of a 60.0-N person (on the moon) can then be found:
m = Fgrav/g = (60.0 N) / (1.63 m/s/s) = 36.7 kg
Since mass is unaffected by location (moon or earth or free space), the mass of the person on earth is the same as the mass on the moon - 36.7 kg.
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
27. Determine the force of gravitational attraction between a 52.0-kg mother and a 3.0-kg child if their separation distance is 0.50 meters. PSYW
|
Answer: 4.2•10-8 N
Use Newton's universal gravitation equation:
Fgrav = G • m1 • m2 /R2 = (6.67•10-11 N•m2/kg2) • (52.0 kg) • (3.0 kg) /(0.50 m)2 = 4.2•10-8 N
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
28. Use the following information to determine the orbital velocity at treetop level on the surface of the moon. PSYW
Mass of moon = 7.36 x 1022 kg
Radius of Moon = 1.74 x 106 m
|
Answer: 1680 m/s
The orbital velocity equation is
v = SQRT(G•Mcentral/R) = SQRT[ (6.67•10-11 N•m2/kg2) • (7.36•1022 kg) / (1.74•106 m) ]
v = SQRT (2.82•106 m2/s2) = 1680 m/s
|
[ #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 ]
Navigate to:
Review Session Home - Topic Listing
Circular Motion and Gravitation - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-14 || #15-28 || #29-40