Sound and Music Review
Navigate to:
Review Session Home - Topic Listing
Sound Waves and Music - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#9 || #10-#52 || #53-#64 || #65-#75
Part C: Problem-Solving and Computational Problems
53. Determine the decibel rating of the following intensities of sound.
- I = 1.0 x 10-5 W/m2
- I = 1.0 x 10-2 W/m2
- I = 6.1 x 10-6 W/m2
- I = 2.2 x 10-4 W/m2
- A sound which is 4 times more intense than the sound in part d.
- A sound which is 7 times more intense than the sound in part d.
- A sound which is 10 times more intense than the sound in part d
- A sound which is 100 times more intense than the sound in part d.
- The sound of an orchestra playing a movement pianissimo at 7.5 x 10-6 W/m2 (very softly)
- The sound of an orchestra playing a movement fortissimo at 2.5 x 10-4 W/m2 (very loudly)
|
Answers: See below
The equation which relates the intensity of a sound wave to its decibel level is:
dB = 10 * log( I / 1.0 x 10-12 W/m2)
where I = intensity of the sound in units of W/m2. Using this equation, parts a - d can be computed in straightforward fashion.
a. dB = 10 * log( 1 x 10-5 W/m2 / 1.0 x 10-12 W/m2) = 70. dB
b. dB = 10 * log( 1 x 10-2 W/m2 / 1.0 x 10-12 W/m2) = 100. dB
c. dB = 10 * log( 6.1 x 10-6 W/m2 / 1.0 x 10-12 W/m2) = 68 dB
d. dB = 10 * log( 2.2 x 10-4 W/m2 / 1.0 x 10-12 W/m2) = 83 dB
e. The intensity is 4 x (2.2 x 10-4 W/m2 ) or 8.8 x 10-4 W/m2 ; so the decibel rating is 89 dB.
f. The intensity is 7 x (2.2 x 10-4 W/m2 ) or 1.54 x 10-3 W/m2 ; so the decibel rating is 92 dB.
g. The intensity is 10 x (2.2 x 10-4 W/m2 ) or 2.2 x 10-3 W/m2 ; so the decibel rating is 93 dB.
h. The intensity is 100 x (2.2 x 10-4 W/m2 ) or 2.2 x 10-2 W/m2 ; so the decibel rating is 103 dB.
i. dB = 10 * log( 7.5 x 10-6 W/m2 / 1.0 x 10-12 W/m2) = 69 dB
j. dB = 10 * log( 2.5 x 10-4 W/m2 / 1.0 x 10-12 W/m2) = 84 dB
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
54. A machine produces a sound with an intensity of 2.9 x 10-3 W/m2. What would be the decibel rating if four of these machines occupy the same room?
|
Answer: 101 dB
Four of these machines would be four times as intense as one machine - that would be an intensity of 1.16 x 10-2 W/m2 . The decibel rating is
dB = 10 * log( 1.16 x 10-2 W/m2 / 1 x 10-12 W/m2) = 101 dB
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
55. The sound in the United Center during a Chicago Bulls basketball game in 1998 was seven times as intense as it is today. If the decibel rating today is 89 dB, then what was the intensity rating in 1998?
|
Answer: 5.56 x 10-3 W/m2
This problem involves finding the intensity level in the stadium today and then multiplying it by seven. The conversion from dB to intensity in W/m2 is done using the usual equation.
dB = 10 * log( I / 1 x 10-12 W/m2)
The decibel level is substituted into the equation and then each side is divided by 10.
89 dB = 10 * log( I / 1 x 10-12 W/m2)
8.9 = log( I / 1 x 10-12 W/m2)
Now to solve for I, take the invlog of each side of the equation.
invlog(8.9) = invlog( log( I / 1 x 10-12 W/m2) )
7.94 x 108 = I / 1 x 10-12 W/m2
Now multiply both sides of the equation by 1 x 10-12 W/m2 to solve for I.
7.94 x 10-4 W/m2 = I
Now multiply by 7 since the intensity was seven times greater.
I = 5.56 x 10-3 W/m2
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
56. A sound has an intensity of 8.0 x10-3 W/m2 at a distance of 2.0 m from its source. What is the intensity at a distance of ...
- ... 4.0 m from the source?
- ... 6.0 m from the source?
- ... 8.0 m from the source?
- ... 24.0 m from the source?
- ... 46.1 m from the source?
|
Answers: See below.
This problem tests your understanding of the inverse square law: the intensity of a sound varies inversely with the square of the distance from the source of the sound.
I = k • (1/R2)
a. As the distance is doubled (4 m is two times 2 m), the intensity level is reduced by a factor of 4. The new intensity is 8.0 x10-3 W/m2/ 4 = 2.0 x10-3 W/m2.
b. As the distance is tripled (6 m is three times 2 m), the intensity level is reduced by a factor of 9. The new intensity is 8.0 x10-3 W/m2/ 9 = 8.9 x10-4 W/m2.
c. As the distance is quadrupled (8 m is four times 2 m), the intensity level is reduced by a factor of 16. The new intensity is 8.0 x10-3 W/m2/ 16 = 5.0 x10-4 W/m2.
d. As the distance is increased by a factor of 12 (24 m is 12 times 2 m), the intensity level is reduced by a factor of 144. The new intensity is 8.0 x10-3 W/m2/ 144 = 1.4 x10-5 W/m2.
e. As the distance is increased by a factor of 23.05 (46.1 m is 23.05 times 2 m), the intensity level is reduced by a factor of 531. The new intensity is 8.0 x10-3 W/m2/ 531 = 1.5 x10-5 W/m2.
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
57. Ben Stupid is sitting 2.0 m in front of the speakers on the stage at the Twisted Brother concert. The decibel rating of the sound heard there is 110 dB. What would be the decibel rating at a location of ...
- ... 4.0 m from the speaker?
- ... 6.0 m from the speaker?
- ... 20.0 m from the speaker?
|
Answer: See answers below.
This problem is similar to the last problem in that it tests your understanding of the inverse square law. There is however a slight twist. The decibel rating is given and since the decibel scale is logarithmic, we must first find the intensity level before we do the division. A decibel rating of 110 db is equivalent to an intensity level of 1011 times the threshold of hearing (1 x 10-12 W/m2). So the intensity level at 2.0 m from the speaker is 0.1 W/m2. Now the inverse square law is applied; the intensity of a sound varies inversely with the square of the distance from the source of the sound.
I = k • (1/R2)
a. As the distance is doubled (4 m is two times 2 m), the intensity level is reduced by a factor of 4. The new intensity is 0.1 W/m2/ 4 = 0.025 W/m2 or 2.5 x10-2 W/m2. This converts to a decibel rating of 104 dB.
b. As the distance is tripled (6 m is three times 2 m), the intensity level is reduced by a factor of 9. The new intensity is 0.1 W/m2/ 9 = 0.011 W/m2 or 1.1 x10-2 W/m2. This converts to a decibel rating of 101 dB (100.5 dB).
c. As the distance is increased by a factor of 10 (20 m is 10 times 2 m), the intensity level is reduced by a factor of 100. The new intensity is 0.1 W/m2/ 100 = 0.0010 W/m2 or 1.0 x10-3 W/m2. This converts to a decibel rating of 90 dB.
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
58. Use the Doppler equation for a moving source to calculate the observed frequency for a 250.-Hz source of sound if it is moving with a speed of ____ . (Assume that the speed of sound in air is 340. m/s.)
- 30. m/s towards the observer.
- 30. m/s away from the observer.
- 300. m/s towards the observer.
- 300. m/s away from the observer.
- 320. m/s towards the observer.
- 335 m/s towards the observer.
|
Answers: See below.
The Doppler equation for determining the observed frequency for a moving source is:
fobserved = vsound / (vsound ± vsource) •fsource
The + sign is used if the source moves away from the observer
The - sign is used if the source moves towards the observer.
If applied to this situation, vsound is 340 m/s and fsource is 250 Hz.
a. fobserved = (340. m/s)/(340. m/s - 30. m/s) • (250 Hz) = (340. m/s)/(310. m/s) • (250. Hz) = 274 Hz
b. fobserved = (340. m/s)/(340. m/s + 30. m/s) • (250 Hz) = (340. m/s)/(370. m/s) • (250. Hz) = 230. Hz
c. fobserved = (340. m/s)/(340. m/s - 300. m/s) • (250 Hz) = (340. m/s)/(40. m/s) • (250. Hz) = 2130 Hz (2125 Hz)
d. fobserved = (340. m/s)/(340. m/s + 300. m/s) • (250 Hz) = (340. m/s)/(640. m/s) • (250. Hz) = 133 Hz
e. fobserved = (340. m/s)/(340. m/s - 320. m/s) • (250 Hz) = (340. m/s)/(20. m/s) • (250. Hz) = 4250 Hz
f. fobserved = (340. m/s)/(340. m/s - 335 m/s) • (250 Hz) = (340. m/s)/(5 m/s) • (250. Hz) = 1.70 x 104 Hz
|
|
Useful Web Links
|
|
None Currently Available
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
59. Shirley Yackin is holding the phone cord in her hand. It is stretched to a length of 2.4 m and has a mass of 1.8 kg. If the tension in the phone cord is 2.5 N, then determine the speed of vibrations within the cord.
|
Answer: 1.8 m/s
The telephone cord acts as a guitar string. As such the speed of waves in the cord is given by the equation
v = SQRT(Ftens/ mu)
where Ftens is the tension in the cord in Newtons and mu is the linear density in kg/m. The tension is given and the mu value can be calculated:
mu = mass/length = (1.8 kg) / (2.4 m) = 0.75 kg/m
Now substitute mu and Ftens into the equation and solve for speed:
v = SQRT[(2.5 N) / (0.75 kg/m)] = SQRT(3.33) = 1.8 m/s (1.8257... m/s)
|
|
Useful Web Links
|
None Currently Available
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
60. (Referring to problem #59.) With what frequency must Shirley vibrate the cord up and down in order to produce the second harmonic within the cord?
|
Answer: 0.76 Hz
 If Shirley is producing the second harmonic, then there will be one full wavelength in the length of the cord. Since the length of the cord is 2.4 m, the wavelength is 2.4 m as well (see diagram at right). With the wavelength and speed (problem #59) known, the frequency can be calculated. (Note that the unrounded number from problem #59 is used i this calculation.) If Shirley is producing the second harmonic, then there will be one full wavelength in the length of the cord. Since the length of the cord is 2.4 m, the wavelength is 2.4 m as well (see diagram at right). With the wavelength and speed (problem #59) known, the frequency can be calculated. (Note that the unrounded number from problem #59 is used i this calculation.)
f = v / lambda = (1.8257 m/s) / (2.4 m) = 0.76 Hz (0.7607... Hz)
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
61. (Referring to problem #60.) If Shirley maintains this same frequency and wishes to produce the fourth harmonic, then she will have to alter the speed of the wave by changing the tension. Assuming the same mass density as in #59, and the same frequency as in #60, to what tension must the cord be pulled to produce the fourth harmonic?
|
Answer: 0.63 N
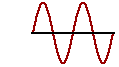 In this case, Shirley is changing the medium. So she is producing the fourth harmonic in a different medium (different properties) using the same frequency as in #60. For the fourth harmonic, there are two full wavelengths inside the length of the cord (see diagram at right); so the length of the wave (wavelength) is one-half the length of the cord - 1.2 m. With frequency and wavelength known, the speed can be computed: In this case, Shirley is changing the medium. So she is producing the fourth harmonic in a different medium (different properties) using the same frequency as in #60. For the fourth harmonic, there are two full wavelengths inside the length of the cord (see diagram at right); so the length of the wave (wavelength) is one-half the length of the cord - 1.2 m. With frequency and wavelength known, the speed can be computed:
v = f • lambda = (0.7607 Hz) • (1.2 m) = 0.91287... m/s.
Now with speed and mu known, the tension can be calculated from the equation:
v = SQRT(Ftens/ mu)
First, perform algebra to manipulate the equation into a form with Ftens by itself. This is done by squaring both sides of the equation and multiplying by mu.
v2 = Ftens/ mu
mu • v2 = Ftens
Now substitute and solve:
Ftens = (0.75 kg/m) • ( 0.91287... m/s)2 = 0.63 N (0.6250 N)
|
|
Useful Web Links
|
|
None Currently Available
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
62. A guitar string has a mass of 32.4 g and a length of 1.12 m. The string is pulled to a tension of 621 N. Determine the speed at which vibrations move within the string.
|
Answer: 147 m/s
This problem is very similar to question #59. The speed of waves in the guitar string is given by the equation
v = SQRT(Ftens/ mu)
where Ftens is the tension in the string in Newtons and mu is the linear density in kg/m. The tension is given and the mu value can be calculated (one will have to be careful of units):
mu = mass/length = (0.0324 kg) / (1.12 m) = 0.0289 kg/m
Now substitute mu and Ftens into the equation and solve for speed:
v = SQRT [ (621 N)/(0.0289 kg/m) ] = SQRT(21467) = 147 m/s (146.515... m/s)
|
|
Useful Web Links
|
|
None Currently Available
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
63. (Referring to problem #62.) Stan Dingwaives is playing this guitar. If Stan leaves the string "open" and uses its full length to produce the first harmonic, then what frequency will Stan be playing?
|
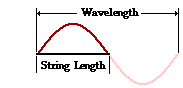 Answer: 65.4 Hz Answer: 65.4 Hz
For the first harmonic, there is only one-half of a wave inside of the length of the string. So the length of the wave is two times longer than the length of the string (see diagram at right). Thus, the wavelength is 2.24 m. Now with speed and wavelength known, the frequency can be calculated.
f = v /lambda = (146.515... m/s) / (2.24 m) = 65.4 Hz (65.4085... Hz)
|
|
Useful Web Links
|
|
None Currently Available
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
64. (Referring to problem #62 and# 63.) If Stan wishes to increase the frequency by a factor of 1.2599, then how far (in cm) from the end of the string must he "close" the string (i.e., where must he press his finger down to change the length and produce the desired frequency)? Use the same mass density and speed as in problem #62.
|
Answer: 0.23 m
For the same speed (same properties of the medium), frequency and wavelength are inversely related. Increasing the frequency by a factor of 1.2599 will be the result of decreasing the wavelength by the same factor. So the new wavelength will be
lambda = (2.24 m) / 1.2599 = 1.78 m
Since the wavelength is twice the effective length of the string, the string must have an effective length of 0.89 m or 89 cm. So, Stan must place his finger a distance of 0.23 m or 23 cm (1.12 m - 0.89 m) from the end of the string.
|
[ #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 ]
Navigate to:
Review Session Home - Topic Listing
Sound Waves and Music - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#9 || #10-#52 || #53-#64 || #65-#75
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Sound and Music
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 5 of the series includes topics on Sound Waves and Music.
Visit: MOP the App Home || MOP the App - Part 5