During a collision, an object experiences an impulse that changes its momentum. The impulse is equal to the momentum change. Knowing that impulse is the product of Force•∆Time and that momentum change is the product of Mass•∆Velocity, one can use the Force•∆Time = Mass•∆Velocity relationship as a guide to thinking about how alterations in m, ∆t, and ∆v affect the force in a collision.
Case Studies: Impulse and Force - Questions 3 Help
Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
There are two very similar versions of this question. This is one of the two versions:
Version 1
Compare these two collisions of a PE student with a wall.
Case A: A 75-kg PE student moving at 8 m/s collides with an unpadded wall and stops.
Case B: The same 75-kg PE student moving at 8 m/s collides with a padded wall and stops.
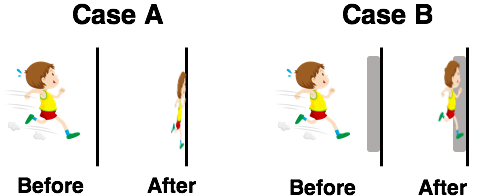
Which variable is different for these two cases?
Which case involves the greatest momentum change? … the greatest impulse? … the greatest force?
Try the links below to our Tutorial for more information:
Momentum and Impulse Connections