Getting your Trinity Audio player ready...

Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.

Case Studies: Electric Power - help13

The power rating of a light bulb indicates the rate at which that bulb emits light energy. It is sometimes referred to as the wattage of the bulb. A bulb with a greater power rating will be a brighter bulb. The power rating depends upon the bulb's resistance. But it also depends upon the voltage of the battery. These two variables - battery voltage and bulb resistance - influence the current that is in the bulb. So to summarize, the power rating of a bulb or bulb brightness can be related to the battery voltage, the bulb's resistance, and the current in the bulb.

There are two similar versions of this question. Here is one of the versions:

Version 1:
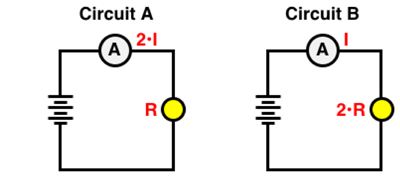
The current in Circuit A is two times the current in Circuit B. The light bulb in Circuit A has one-half the resistance of the light bulb in Circuit B. Which circuit has the greatest power? ... and by what factor?

What Affects Power?
The power rating of a light bulb in this simple circuit depends upon the battery voltage (not mentioned in the question) and the bulb resistance (R). The current (I) in the bulb depends on the battery voltage; and the current is mentioned in the question. To determine which circuit has the most power and the factor by which it is greatest, you need to understand and apply the math relationship between power (brightness), current, and resistance.

The Relationship and Its Application
The relationship between power (P), current (I) and resistance (R) is given by the equation ...

P = I²•R

As should be obvious from the equation, a larger current results in a larger power. And a larger resistance also results in a larger power. But in this question, one circuit has the larger current and the other circuit has the larger resistance. So at first glance, you might think that it is a tie. But not so fast! Observe that there is a second power after the I in the equation. This squaring of current means that a doubling of the current results in a quadrupling of the power. Contrast this with the fact that the power only doubles when the resistance is doubled. So the circuit with the greatest power is the one with the greatest current. To determine the factor by which its power is greater consider the fact that the larger current causes its power to quadruple while the smaller resistance causes the power to half. Put these two competing factors together to complete the answer to this question.

Try these links to The Physics Classroom Tutorial for more help with understanding power and the factors that affect it:

Power: Putting the Charges to Work

Electric Power Revisited