The power rating of a light bulb indicates the rate at which that bulb emits light energy. It is sometimes referred to as the wattage of the bulb. A bulb with a greater power rating will be a brighter bulb. The power rating depends upon the bulb's resistance. But it also depends upon the voltage of the battery. These two variables - battery voltage and bulb resistance - influence the current that is in the bulb. So to summarize, the power rating of a bulb or bulb brightness can be related to the battery voltage, the bulb's resistance, and the current in the bulb.
Getting your Trinity Audio player ready...
Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Case Studies: Electric Power - help15
There are two similar versions of this question. This is one of those versions.
Version 1:
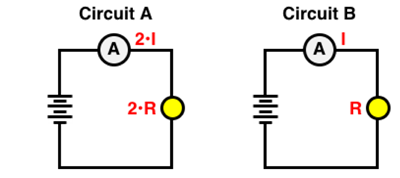
The current in Circuit A is two times the current in Circuit B. The light bulb in Circuit A has two times the resistance of the light bulb in Circuit B. Which circuit has the greatest power? ... and by what factor?
Try these links to The Physics Classroom Tutorial for more help with understanding power and the factors that affect it:
Power: Putting the Charges to Work
Electric Power Revisited