A force analysis for an object accelerating along an inclined plane is typically done by determining the value of all he forces that are directed parallel and perpendicular to the inclined plane. Friction forces are always parallel to the inclined plane. Normal forces are always perpendicular to the inclined plane. But the gravity force is straight down, directed at an acute angle to the inclined plane. This force must be resolved into a parallel component and a perpendicular component. Once done, oppositely-directed forces can be easily summed to determine the net force and the acceleration.
 

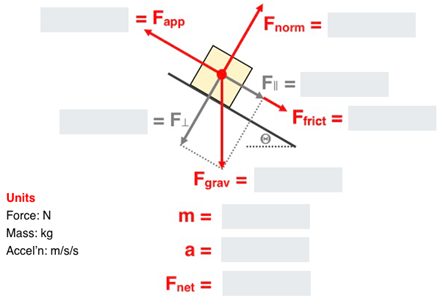
The two situations in this Difficulty Level are identical; only the numbers are different. There is an object accelerating up an inclined plane as the result of an applied force. The object mass, the incline angle, the applied force, and the coefficient of friction are stated.  You must determine the parallel- and perpendicular-components, the force of gravity, the normal force, the friction force, the net force and the acceleration. You can enter one value at a time and check its correctness or enter several values and check their correctness all at once. However you proceed, you will need to be mindful of the relationships between the various quantities. That's what this Help page is about. Our suggestions follow.


First Things First
There are four values provided; two of them matches with blanks. Read the Analyze This statement carefully, extract the numerical values and associate them with the quantities they represent. This is always the recommended starting point for any effective problem-solving strategy - identify what you know. Get that correct and you should have seven blanks left.

 

Understand the Gravity of the Situation
One of the blanks is the mass (m) and another blank is the weight or force of gravity (F_grav). And hopefully you know that they are related and you know the relationship. And if you don't, take some time to think about this relationship before you complete the analysis. It's a big thing in Physics. If it's confusing you now, it will confuse you later until you take the time to unconfuse yourself. The relationship is ...

F_grav = m•g
where g = gravitational field strength (on Earth, approximately 9.8 N/kg)

The force of gravity is sometimes called the weight. It's value depends upon the mass of the object and the gravitational environment where the object is located. The g is called many things (some more accurate than others). But you should recognize that it reveals something about the gravitational environment where the object is located (probably, Earth). An on planet Earth, the value of g is 9.8 N/kg. Use this info to find one more blank. And if you needed the equation to do this, then do yourself a favor and spend some time digesting this paragraph.


 

Resolve the Gravity Force into Components
The object accelerates parallel to the inclined plane. So you need to know all the force information in this plane. And it helps to also know all the perpendicular force information as well. The force that is neither parallel nor perpendicular to the plane is the force of gravity. It's the force that makes this situation problematic.But don't worry. Vector components are coming to the rescue.

So your next task is to use the magnitude of the gravity force (F_grav) and the incline angle (θ) to determine what the Fparallel and Fperpendicular values are. The equations for doing this are ...

F_{perpendicular} = F_grav • cosine θ

Fparallel = F_grav • sine θ

Perform the calculations, enter the values, and narrow down the missing blanks to four. And before you go on, here's a TIP: Now that you have resolved the gravity force into two components, forget about the gravity force. Disregard it. It's no longer important! It's called substitution. The applied force has been taken out of the ball game and replaced by two components. So don't worry about F_app. Do worry about Fparallel and Fperpendicular. The components are now the players in the game.

 

Always Be Principled
A normal force (F_norm) is always directed perpendicular to the surface that the object rests upon. This is the force of the supporting surface pushing up on the object. You might be conditioned to quickly equate it with F_grav. That is, you might have something in your head that says ..."The normal force is always equal to the gravity force." THAT'S WRONG. It's often true that the normal force is equal to the gravity force but it is NOT ALWAYS TRUE (excuse the capitals here ... they're needed for needed emphasis). So read carefully:

If the normal force and the gravity force are both vertical forces and if they are the only vertical forces and if there is no vertical acceleration ...
Then the normal force is equal to the gravity force.

Now that's a lot of IFs. But the Physics principle in the statement is that vertical forces balance when there is no vertical acceleration. In our problem, we're not thinking about horizontal and vertical because the acceleration is neither horizontal nor vertical. The acceleration is parallel to the inclined plane. And so we think in terms of parallel and perpendicular forces. And when it comes to the acceleration, it is parallel to the inclined plane and not perpendicular to it. So in this case, the perpendicular forces balance. That is the normal force and the perpendicular component of gravity are balanced.

F_{perpendicular} = F_norm

So now you can enter the normal force and narrow the number of blanks down to three. And before you go much further, take a moment to think about the logic behind how you determined the normal force - that is, the logic that led to the equation above. You got this!

 

 

What's That Fricken µ Symbol Mean?
Excuse me but that fricken symbol is a friction symbol and it's called the coefficient of friction. It's a Greek letter; we Physics types call it "mu".  (We even make cat and cow jokes about it ... but that's another story.) Mu or µ is not a force. It is a ratio of two forces. It's the ratio of the friction force to the normal force. It is specific to the two surfaces that slide across each other. It tells us how many Newtons of friction force that there are for every 1.00 N of force pressing the surfaces together (i.e., normal force). The useful equation that describes all this is ...

F_frict= µ•F_norm

You can (and should) use this equation to calculate the friction force. Do note though that the equation requires that you multiply the coefficient of friction (µ) by the normal force ... and not by the gravity force or any other force.



Things Go Better With Newton
Two blanks left - net force (F_net) and acceleration (a). The net force is always the vector sum of all the individual forces; some teachers refer to it as ∑F. The perpendicular-to-the-incline forces sum to zero; that is they're balanced (mentioned above). So focus on the parallel-to-the-incline forces. There is only one of these as shown on the force diagram - Fparallel. So that ought to make the "summing" quite easy. The net force or vector sum of the forces is simply equal to the parallel component of gravity. 

The F_x value is bigger; it is causing the acceleration. The F_frict  goes the opposite direction; it is opposing the acceleration. When you sum these two forces, you must call F_x positive and F_frict negative since they are directed in opposite directions. And so ...

F_net = ∑F = F_x - F_frict

Now that you know the net force, the acceleration can easily be determined using the Newton's second law equation ...

a = F_net / m

Hey ... One More Thing ... and Perhaps the Most Important Thing
If you relied on this Help page to do the first situation of the two situations in this Master Difficulty Level, then try this: Study your solution before you tap on the Check Answers button. Review all the logic. Then complete the second analysis without any reference to this page. That's how you learn! And that's how you know you learned!