Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
In Unit 2 of The Physics Classroom, an equation was given for determining the force of gravity (Fgrav) with which an object of mass m was attracted to the earth
Fgrav = m*g
Now in this unit, a second equation has been introduced for calculating the force of gravity with which an object is attracted to the earth.
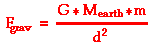
where d represents the distance from the center of the object to the center of the earth.
 In the first equation above, g is referred to as the acceleration of gravity. Its value is 9.8 m/s2 on Earth. That is to say, the acceleration of gravity on the surface of the earth at sea level is 9.8 m/s2. When discussing the acceleration of gravity, it was mentioned that the value of g is dependent upon location. There are slight variations in the value of g about earth's surface. These variations result from the varying density of the geologic structures below each specific surface location. They also result from the fact that the earth is not truly spherical; the earth's surface is further from its center at the equator than it is at the poles. This would result in larger g values at the poles. As one proceeds further from earth's surface - say into a location of orbit about the earth - the value of g changes still.
In the first equation above, g is referred to as the acceleration of gravity. Its value is 9.8 m/s2 on Earth. That is to say, the acceleration of gravity on the surface of the earth at sea level is 9.8 m/s2. When discussing the acceleration of gravity, it was mentioned that the value of g is dependent upon location. There are slight variations in the value of g about earth's surface. These variations result from the varying density of the geologic structures below each specific surface location. They also result from the fact that the earth is not truly spherical; the earth's surface is further from its center at the equator than it is at the poles. This would result in larger g values at the poles. As one proceeds further from earth's surface - say into a location of orbit about the earth - the value of g changes still.
The Value of g Depends on Location
To understand why the value of g is so location dependent, we will use the two equations above to derive an equation for the value of g. First, both expressions for the force of gravity are set equal to each other.
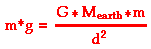
Now observe that the mass of the object - m - is present on both sides of the equal sign. Thus, m can be canceled from the equation. This leaves us with an equation for the acceleration of gravity.
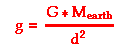
The above equation demonstrates that the acceleration of gravity is dependent upon the mass of the earth (approx. 5.98x1024 kg) and the distance (d) that an object is from the center of the earth. If the value 6.38x106 m (a typical earth radius value) is used for the distance from Earth's center, then g will be calculated to be 9.8 m/s2. And of course, the value of g will change as an object is moved further from Earth's center. For instance, if an object were moved to a location that is two earth-radii from the center of the earth - that is, two times 6.38x106 m - then a significantly different value of g will be found. As shown below, at twice the distance from the center of the earth, the value of g becomes 2.45 m/s2.
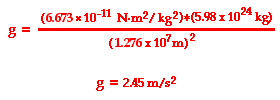
The table below shows the value of g at various locations from Earth's center.
|
Location
|
Distance from Earth's center
(m)
|
Value of g
(m/s2)
|
|
Earth's surface
|
6.38 x 106 m
|
9.8
|
|
1000 km above surface
|
7.38 x 106 m
|
7.33
|
|
2000 km above surface
|
8.38 x 106 m
|
5.68
|
|
3000 km above surface
|
9.38 x 106 m
|
4.53
|
|
4000 km above surface
|
1.04 x 107 m
|
3.70
|
|
5000 km above surface
|
1.14 x 107 m
|
3.08
|
|
6000 km above surface
|
1.24 x 107 m
|
2.60
|
|
7000 km above surface
|
1.34 x 107 m
|
2.23
|
|
8000 km above surface
|
1.44 x 107 m
|
1.93
|
|
9000 km above surface
|
1.54 x 107 m
|
1.69
|
|
10000 km above surface
|
1.64 x 107 m
|
1.49
|
|
50000 km above surface
|
5.64 x 107 m
|
0.13
|
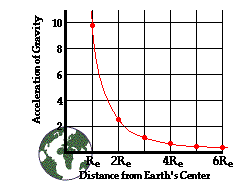
As is evident from both the equation and the table above, the value of g varies inversely with the distance from the center of the earth. In fact, the variation in g with distance follows an inverse square law where g is inversely proportional to the distance from earth's center. This inverse square relationship means that as the distance is doubled, the value of g decreases by a factor of 4. As the distance is tripled, the value of g decreases by a factor of 9. And so on. This inverse square relationship is depicted in the graphic at the right.
Calculating g on Other Planets
The same equation used to determine the value of g on Earth' surface can also be used to determine the acceleration of gravity on the surface of other planets. The value of g on any other planet can be calculated from the mass of the planet and the radius of the planet. The equation takes the following form:

Using this equation, the following acceleration of gravity values can be calculated for the various planets.
|
Planet
|
Radius (m)
|
Mass (kg)
|
g (m/s2)
|
|
Mercury
|
2.43 x 106
|
3.2 x 1023
|
3.61
|
|
Venus
|
6.073 x 106
|
4.88 x1024
|
8.83
|
|
Mars
|
3.38 x 106
|
6.42 x 1023
|
3.75
|
|
Jupiter
|
6.98 x 107
|
1.901 x 1027
|
26.0
|
|
Saturn
|
5.82 x 107
|
5.68 x 1026
|
11.2
|
|
Uranus
|
2.35 x 107
|
8.68 x 1025
|
10.5
|
|
Neptune
|
2.27 x 107
|
1.03 x 1026
|
13.3
|
|
Pluto
|
1.15 x 106
|
1.2 x 1022
|
0.61
|
The acceleration of gravity of an object is a measurable quantity. Yet emerging from Newton's universal law of gravitation is a prediction that states that its value is dependent upon the mass of the Earth and the distance the object is from the Earth's center. The value of g is independent of the mass of the object and only dependent upon location - the planet the object is on and the distance from the center of that planet.
Even on the surface of the Earth, there are local variations in the value of g. These variations are due to latitude (the Earth isn't a perfect sphere; it buldges in the middle), altitude and the local geological structure of the region. Use the Gravitational Fields widget below to investigate how location affects the value of g. And for a more visual experience, try the related Value of g Interactive from the Physics Interactives section of our website.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Gravitation Interactive and/or our
Value of g on Other Planets Interactive. You can find these in the Physics Interactives section of our website. Both Interactives allow a learner to interactively explore the effect of planet characteristics upon the gravitational field.