Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 Previously in Lesson 3, ray diagrams were constructed in order to determine the general location, size, orientation, and type of image formed by concave mirrors. Perhaps you noticed that there is a definite relationship between the image characteristics and the location where an object is placed in front of a concave mirror. The purpose of this portion of the lesson is to summarize these object-image relationships - to practice the L•O•S•T art of image description. We wish to describe the characteristics of the image for any given object location. The L of L•O•S•T represents the relative location. The O of L•O•S•T represents the orientation (either upright or inverted). The S of L•O•S•T represents the relative size (either magnified, reduced or the same size as the object). And the T of L•O•S•T represents the type of image (either real or virtual). The
Previously in Lesson 3, ray diagrams were constructed in order to determine the general location, size, orientation, and type of image formed by concave mirrors. Perhaps you noticed that there is a definite relationship between the image characteristics and the location where an object is placed in front of a concave mirror. The purpose of this portion of the lesson is to summarize these object-image relationships - to practice the L•O•S•T art of image description. We wish to describe the characteristics of the image for any given object location. The L of L•O•S•T represents the relative location. The O of L•O•S•T represents the orientation (either upright or inverted). The S of L•O•S•T represents the relative size (either magnified, reduced or the same size as the object). And the T of L•O•S•T represents the type of image (either real or virtual). The 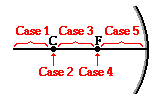 best means of summarizing this relationship between object location and image characteristics is to divide the possible object locations into five general areas or points:
best means of summarizing this relationship between object location and image characteristics is to divide the possible object locations into five general areas or points:
- Case 1: the object is located beyond the center of curvature (C)
- Case 2: the object is located at the center of curvature (C)
- Case 3: the object is located between the center of curvature (C) and the focal point (F)
- Case 4: the object is located at the focal point (F)
- Case 5: the object is located in front of the focal point (F)
Case 1: The object is located beyond C
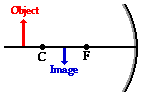 When the object is located at a location beyond the center of curvature, the image will always be located somewhere in between the center of curvature and the focal point. Regardless of exactly where the object is located, the image will be located in the specified region. In this case, the image will be an inverted image. That is to say, if the object is right side up, then the image is upside down. In this case, the image is reduced in size; in other words, the image dimensions are smaller than the object dimensions. If the object is a six-foot tall person, then the image is less than six feet tall. Earlier in Lesson 2, the term magnification was introduced; the magnification is the ratio of the height of the image to the height of the object. In this case, the absolute value of the magnification is less than 1. Finally, the image is a real image. Light rays actually converge at the image location. If a sheet of paper were placed at the image location, the actual replica of the object would appear projected upon the sheet of paper.
When the object is located at a location beyond the center of curvature, the image will always be located somewhere in between the center of curvature and the focal point. Regardless of exactly where the object is located, the image will be located in the specified region. In this case, the image will be an inverted image. That is to say, if the object is right side up, then the image is upside down. In this case, the image is reduced in size; in other words, the image dimensions are smaller than the object dimensions. If the object is a six-foot tall person, then the image is less than six feet tall. Earlier in Lesson 2, the term magnification was introduced; the magnification is the ratio of the height of the image to the height of the object. In this case, the absolute value of the magnification is less than 1. Finally, the image is a real image. Light rays actually converge at the image location. If a sheet of paper were placed at the image location, the actual replica of the object would appear projected upon the sheet of paper.
Case 2: The object is located at C
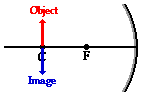 When the object is located at the center of curvature, the image will also be located at the center of curvature. In this case, the image will be inverted (i.e., a right side up object results in an upside-down image). The image dimensions are equal to the object dimensions. A six-foot tall person would have an image that is six feet tall; the absolute value of the magnification is equal to 1. Finally, the image is a real image. Light rays actually converge at the image location. As such, the image of the object could be projected upon a sheet of paper.
When the object is located at the center of curvature, the image will also be located at the center of curvature. In this case, the image will be inverted (i.e., a right side up object results in an upside-down image). The image dimensions are equal to the object dimensions. A six-foot tall person would have an image that is six feet tall; the absolute value of the magnification is equal to 1. Finally, the image is a real image. Light rays actually converge at the image location. As such, the image of the object could be projected upon a sheet of paper.
Case 3: The object is located between C and F
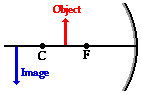 When the object is located in front of the center of curvature, the image will be located beyond the center of curvature. Regardless of exactly where the object is located between C and F, the image will be located somewhere beyond the center of curvature. In this case, the image will be inverted (i.e., a right side up object results in an upside-down image). The image dimensions are larger than the object dimensions. A six-foot tall person would have an image that is larger than six feet tall; the absolute value of the magnification is greater than 1. Finally, the image is a real image. Light rays actually converge at the image location. As such, the image of the object could be projected upon a sheet of paper.
When the object is located in front of the center of curvature, the image will be located beyond the center of curvature. Regardless of exactly where the object is located between C and F, the image will be located somewhere beyond the center of curvature. In this case, the image will be inverted (i.e., a right side up object results in an upside-down image). The image dimensions are larger than the object dimensions. A six-foot tall person would have an image that is larger than six feet tall; the absolute value of the magnification is greater than 1. Finally, the image is a real image. Light rays actually converge at the image location. As such, the image of the object could be projected upon a sheet of paper.
Case 4: The object is located at F
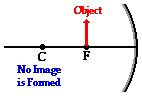 When the object is located at the focal point, no image is formed. As discussed earlier in Lesson 3, light rays from the same point on the object will reflect off the mirror and neither converge nor diverge. After reflecting, the light rays are traveling parallel to each other and do not result in the formation of an image.
When the object is located at the focal point, no image is formed. As discussed earlier in Lesson 3, light rays from the same point on the object will reflect off the mirror and neither converge nor diverge. After reflecting, the light rays are traveling parallel to each other and do not result in the formation of an image.
Case 5: The object is located in front of F
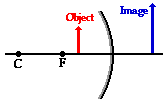 When the object is located at a location beyond the focal point, the image will always be located somewhere on the opposite side of the mirror. Regardless of exactly where in front of F the object is located, the image will always be located behind the mirror. In this case, the image will be an upright image. That is to say, if the object is right side up, then the image will also be right side up. In this case, the image is magnified; in other words, the image dimensions are greater than the object dimensions. A six-foot tall person would have an image that is larger than six feet tall; the magnification is greater than 1. Finally, the image is a virtual image. Light rays from the same point on the object reflect off the mirror and diverge upon reflection. For this reason, the image location can only be found by extending the reflected rays backwards beyond the mirror. The point of their intersection is the virtual image location. It would appear to any observer as though light from the object were diverging from this location. Any attempt to project such an image upon a sheet of paper would fail since light does not actually pass through the image location.
When the object is located at a location beyond the focal point, the image will always be located somewhere on the opposite side of the mirror. Regardless of exactly where in front of F the object is located, the image will always be located behind the mirror. In this case, the image will be an upright image. That is to say, if the object is right side up, then the image will also be right side up. In this case, the image is magnified; in other words, the image dimensions are greater than the object dimensions. A six-foot tall person would have an image that is larger than six feet tall; the magnification is greater than 1. Finally, the image is a virtual image. Light rays from the same point on the object reflect off the mirror and diverge upon reflection. For this reason, the image location can only be found by extending the reflected rays backwards beyond the mirror. The point of their intersection is the virtual image location. It would appear to any observer as though light from the object were diverging from this location. Any attempt to project such an image upon a sheet of paper would fail since light does not actually pass through the image location.
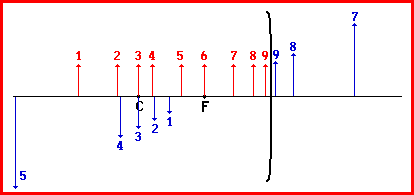
It might be noted from the above descriptions that there is a relationship between the object distance and object size and the image distance and image size. Starting from a large value, as the object distance decreases (i.e., the object is moved closer to the mirror), the image distance increases; meanwhile, the image height increases. At the center of curvature, the object distance equals the image distance and the object height equals the image height. As the object distance approaches one focal length, the image distance and image height approaches infinity. Finally, when the object distance is equal to exactly one focal length, there is no image. Then altering the object distance to values less than one focal length produces images that are upright, virtual and located on the opposite side of the mirror. Finally, if the object distance approaches 0, the image distance approaches 0 and the image height ultimately becomes equal to the object height. These patterns are depicted in the diagram below. Nine different object locations are drawn and labeled with a number; the corresponding image locations are drawn in blue and labeled with the identical number.
We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Optics Bench Interactive or our
Name That Image Interactive. You can find this in the Physics Interactives section of our website. The
Optics Bench Interactive provides the learner an interactive enivronment for exploring the formation of images by lenses and mirrors. The
Name That Image Interactive provides learners with an intensive mental workout in recognizing the image characteristics for any given object location in front of a curved mirror.
Check Your Understanding
1. Compare and contrast the images formed by concave and plane mirrors.
2. Identify the means by which you can use a concave and/or a plane mirror to form a real image.
3. Identify the means by which you can use a concave and/or a plane mirror to form a virtual image.
4. Identify the means by which you can use a concave and/or a plane mirror to produce an upright image.
5. Identify the means by which you can use a concave and/or a plane mirror to produce an inverted image.
6. Are all real images larger than the object?
7. A famous magician conducts a classic magic trick utilizing a concave mirror with a focal length of 1.6 m. She is able to use the mirror in such a manner as to produce an image of a light bulb at the same location and of the same size as the actual light bulb itself. Use complete sentences to explain how the magician is able to accomplish this magic trick. Be specific about the light bulb location.