Getting your Trinity Audio player ready...

Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.

Fundamentals

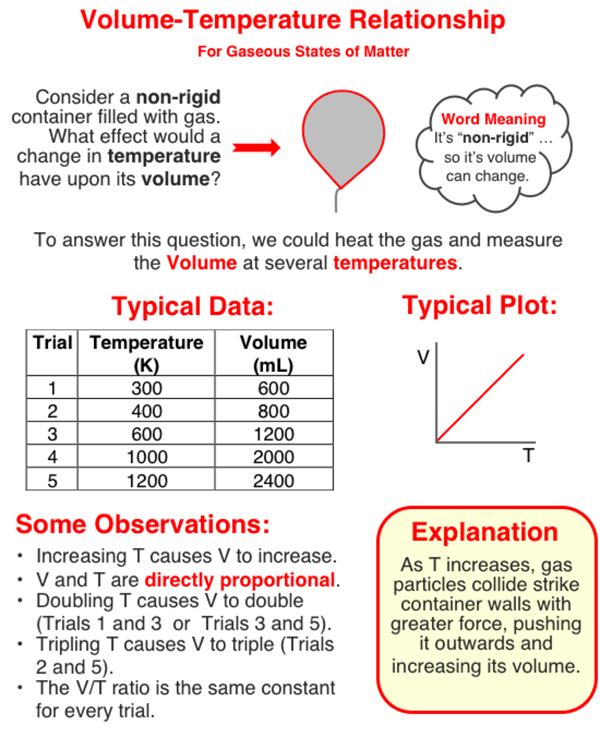
The pressure of a sample of gas is dependent upon the Kelvin temperature of the gas. Increasing the Kelvin temperature increases the pressure. The two quantities are directly proportional to one another. A tripling of the Kelvin temperature will triple the pressure of the gas.

There are two questions in this Question Group. Each question is very similar to one another. The question below is one of the questions.

Version 1:

Observe the data table shown at the right for a sample of gas that has a constant volume and number of particles.  Use the data table to answer the next two questions.
 
When the Kelvin temperature of the gas is tripled (increased by a factor of three), the pressure of the gas becomes _____.
a. three times larger
b. six times larger
c. nine times larger
d. one-third the size
e. one-sixth the size
f. one-ninth the size
g. Not possible to tell
 
Which pairs of trials demonstrate this relationship?  Select all that apply.
a. 1 and 2
b. 1 and 3
c. 1 and 4
d. 1 and 5
e. 2 and 4
f. 2 and 5
g. 3 and 4
h. 3 and 5
 
 

 

 

How to Think About This Situation:

In this question, you need to analyze a set of data to determine the effect that a tripling of Kelvin temperature has upon the pressure of a gas (held at a constant volume). The graphic below will provide some background to the topic. Study (and/or scan) the graphic and then return to the text that continues below the graphic.
 

Tripling Kelvin Temperature

A tripling of temperature occurs between two trials whenever the value of temperature in one trial is three times that of another trial. In the graphic directly above, Trials 2 and 5 are examples of tripling because Trial 5 has a temperature (1200 K) which is tree times that of Trial 2 (400 K). 

So to determine the effect that this tripling has, you will have to look at the corresponding pressure values for these two rows. For instance, the pressure values in the graphic above for Trials 2 and 5 are 800 mm Hg and 2400 mm Hg. Trial 5 's pressure value is three times the value of Trial 2. This indicates that a tripling of the Kelvin temperature leads to a tripling of the pressure of the gas. 

You will need to apply the same type of thinking to the analysis of the Data Set provided in your question. Good luck.
 


Tired of Ads?
Go ad-free for 1 year