How Far Will It Skid?
Most driver's education classes teach future drivers that the stopping distance of a skidding car is directly proportional to the square of the speed of the car. That is a car traveling 10 mi/hr may require 4 feet to skid to an abrupt halt; but a car going twice as fast - 20 mi/hr - would require four times the distance - 16 feet to skid to a stop. A doubling of the speed results in a quadrupling of the stopping distance. A tripling of the speed would increase the stopping distance by a factor of nine. And a quadrupling of the speed would increase the stopping distance by a factor of 16. The stopping distance is proportional to the square of the speed of the vehicle.
This mathematical relationship between initial speed and stopping distance is depicted in the animation below. Three cars with identical braking systems are traveling three different speeds. Prior to braking, the red car is traveling twice as fast as the green car (20 m/s is two times as big as 10 m/s); and prior to braking, the blue car is traveling three times as fast as the green car (30 m/s is three times as big as 10 m/s). The animation depicts that the stopping distance of the red car is four times (22) that of the green car and the stopping distance of the blue car is nine times (32) that of the green car.
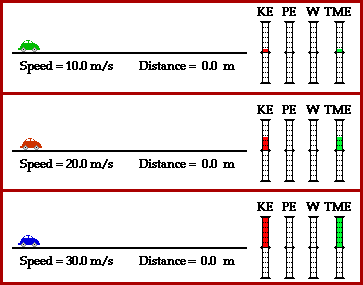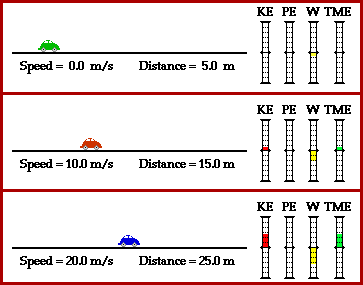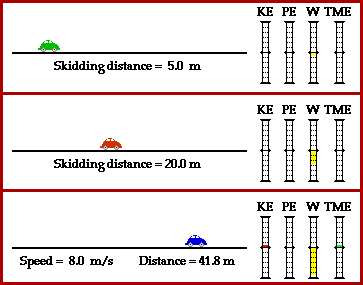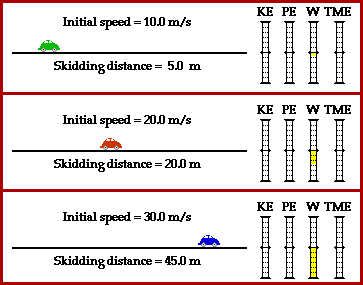
Perhaps you learned in a drivers education course of this mathematical relationship between initial speed and stopping distance. But did you know that the relationship is based upon the physics of work and energy? Prior to braking each car has kinetic energy (energy due to motion). The amount of kinetic energy is dependent upon the mass and the speed of the car according to the equation
KE = 0/5*mass*(speed)2
The blue car has the most kinetic energy since it has the greatest speed. This is portrayed in the work-energy bar charts above by the height of the KE bar for each car.
Once the brakes are applied, the force of friction acts upon the car. The work done by friction on the skidding car is proportional to stopping distance according to the equation
Work = Force * displacement * cosine(Theta)
where the displacement of the car is simply the distance the car skids to a stop and Theta is the angle between the force and the displacement vectors. In this case, Theta is 180 degrees since the force of friction and the displacement of the car are in opposite directions.
The work done by friction on the car is related to the initial kinetic energy of the car. The work-energy relationship is often related by the equation
KEi + PEi + Wext = KEf + PEf
Since the potential energy of the car is the same in the initial state (before braking) as the final state (after stopping), each term can be canceled from the above equation. And since the car is finally stopped, the KEf term in the equation is zero. Thus, the equation becomes
0.5*m*v2 + F*d*cos(180) = 0.
This equation can be rearranged so that it takes the form of
0.5*m*v2 = -F*d*cos(180)
and since the cosine(180) is -1, the equation can be rewritten as
0.5*m*v2 = F*d.
The above equation shows that the stopping distance (d) is proportional to the square of the speed (v2). And that's exactly what the driver's education course taught you. And now you know: it's PHYSICS!
For more information on physical descriptions of motion, visit The Physics Classroom Tutorial. Detailed information is available there on the following topics:
Potential Energy
Kinetic Energy
Mechanical Energy
Internal vs. External Forces
Work
Work-Energy Theorem
Work-Energy Bar Charts