Work and Energy Review
Navigate to:
Review Session Home - Topic Listing
Work and Energy - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-10 || #11-25 || #26-36 || #37-45
Part B: Straightforward Computational Problems
26. Approximate the work required lift a 2.5-kg object to a height of 6.0 meters. PSYW
|
Answer: ~150 J
The work done upon an object is found with the equation
W = F*d*cos(Theta)
In this case, the d=6.0 m; the F=24.5 N (it takes 24.5 N of force to lift a 2.5-kg object; that's the weight of the object), and the angle between F and d (Theta) is 0 degrees. Substituting these values into the above equation yields
W = F*d*cos(Theta) = (24.5 N)*(6 m)*cos(0) = ~150 J (147 J)
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
27. A student applies a force to a cart to pull it up an inclined plane at constant speed during a physics lab. A force of 20.8 N is applied parallel to the incline to lift a 3.00-kg loaded cart to a height of 0.450 m along an incline which is 0.636-m long. Determine the work done upon the cart and the subsequent potential energy change of the cart. PSYW
|
Answer: 13.2 J
There are two methods of solving this problem. The first method involves using the equation
W = F*d*cos(Theta)
where F=20.8 N, d=0.636 m, and Theta=0 degrees. (The angle theta represents the angle betwee the force and the displacement vector; since the force is applied parallel to the incline, the angle is zero.) Substituting and solving yields
W = F*d*cos(Theta) = (20.8 N)*(0.636 m)*cos(0) = 13.2 J.
The second method is to recognize that the work done in pulling the cart along the incline at constant speed changes the potential energy of the cart. The work done equals the potential energy change. Thus,
W=Delta PE = m*g*(delta h) = (3.00 kg)*(9.8 m/s/s)*(0.45 m) = 13.2 J
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
28. Eddy, whose mass is 65.0-kg, climbs up the 1.60-meter high stairs in 1.20 s. Approximate Eddy's power rating. PSYW
|
Answer: P = 849 Watts
Eddy's power is found by dividing the work which he does by the time in which he does it. The work done in elevating his 65.0-kg mass up the stairs is determined using the equation
W = F*d*cos(Theta)
where F = m*g = 637 N (the weight of the 65.0 kg object), d =1.60 m and Theta = 0 degrees (the angle between the upward force and the upward displacement). Solving for W yields 1019.2 Joules. Now divide the work by the time to determine the power:
P = W/t = (1019.2 J)/(1.20 s) = 849 Watts
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
29. A 51.7-kg hiker ascends a 43.2-meter high hill at a constant speed of 1.20 m/s. If it takes 384 s to climb the hill, then determine ... . PSYW
- kinetic energy change of the hiker.
- the potential energy change of the hiker.
- the work done upon the hiker.
- the power delivered by the hiker.
|
Answers:
- Delta KE = 0 J
- Delta PE = +21900 J
- W = +21900 J
- P = 57.0 Watts
a. The speed of the hiker is constant so there is no change in kinetic energy - 0 J.
b. The potential energy change can be found by subtracting the initial PE (0 J) from the final PE (m*g*hf). The final potential energy is 21888 J [from (51.7 kg)*(9.8 m/s/s)*(43.2 m)] and the initial potential energy is 0 J. So Delta PE = +21900 J (rounded from 21888 J).
c. The work done upon the hiker can be found using the work-energy theorem. The equation reduces to
Wnc = PEf
(PEi = 0 J since the hiker starts on the ground; and KEi = KEf since the speed is constant; these two terms can be dropped from the equation since they are equal). The final potential energy is 21888 J [from (51.7 kg)*(9.8 m/s/s)*(43.2 m)]. So W = +21900 J (rounded from 21888 J).
d. The power of the hiker can be found by dividing the work by the time.
P=W/t=(21888 J)/(384 s) = 57.0 Watts
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
30. An 878-kg car skids to a stop across a horizontal surface over a distance of 45.2 m. The average force acting upon the car is 7160 N. Determine ... . PSYW
- the work done upon the car.
- the initial kinetic energy of the car.
- the acceleration of the car.
- the initial velocity of the car.
|
Answers:
- W = -324000 J
- KEi = +324000 J
- a = -8.16 m/s/s
- vi = 27.2 m/s
a. The work done upon the car can be found using the equation
W = F*d*cos(Theta)
where F=7160 N, d=45.2 m, and Theta=180 degrees (the force is in the opposite direction as the displacement). Substituting and solving yields -323632 J (rounded to -324000 J).
b. The initial kinetic energy can be found using the work-energy theorem. The equation reduces to
KEi + Wnc = 0
(PEi and PEf = 0 J since the car is on the ground; and KEf = 0 J since the car is finally stopped). Rearrange the equation and it takes the form KEi = -Wnc . So KEi = +324000 J (rounded from +323632 J).
c. The acceleration of the car can be found using Newton's second law of motion: Fnet = m*a
The friction force is the net force (since the up and down forces balance) and the mass is 878 kg. Substituting and solving yields a = -8.16 m/s/s.
d. The initial velocity of the car can be found using the KE equation: KE = 0.5*m*v2 where m=878 kg and KEi=323632 J. Substituting and solving for velocity (v) yields v = 27.2 m/s. (A kinematic equation could be also used to find the initial velocity.)
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
31. A 510-kg roller coaster car starts at a height of 32.0 m. Assuming negligible energy losses to friction and air resistance, determine the PE, KE, and speed of the car at the various locations (A, B, C, D, and E) along the track.
|
Location
|
Height
(m)
|
PE*
(J)
|
KE*
(J)
|
velocity
(m/s)
|
|
Start
|
32.0
|
160 000 J
|
0 J
|
0
|
|
A
|
28.0
|
140 000 J
|
20 000 J
|
8.9 m/s
|
|
B
|
11.0
|
55 000 J
|
105 000 J
|
20.5 m/s
|
|
C
|
20.0
|
100 000 J
|
60 000 J
|
15.5 m/s
|
|
D
|
5.0
|
25 000 J
|
135 000 J
|
23.2 m/s
|
|
E
|
15.0
|
75 000 J
|
85 000 J
|
18.4 m/s
|
|
F
|
0
|
0 J
|
160 000 J
|
25.3 m/s
|
*rounded to the second significant digit
|
Answers: See above table (answers in red)
The potential energy for every row can be found using the equation PE = m*g*h where m=510 kg and g = 9.8 m/s/s. In the first row, the total mechanical energy (KE + PE) equals 160 000 J (rounded). Since no work is done by non-conservative forces, the total mechanical energy must be 160 000 J in all the other rows. So the KE can be computed by subtracting the PE from 160 000 J. The velocity can be found using the equation:
KE = 0.5*m*v2
where m=510 kg. The algebraic rearrangement of this equation results in v = SQRT(2*KE/m).
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
32. A 65.8-kg skier accelerates down an icy hill from an original height of 521 meters. Use the work-energy theorem to determine the speed at the bottom of the hill if...
a. ... no energy is lost or gained due to friction, air resistance and other non-conservative forces. PSYW
b. ... 1.40*105 J of energy are lost due to external forces. PSYW
|
Answers: (a) v = 101 m/s; (b) v = 77.2 m/s
a. Use the work energy theorem:
KEi + PEi + Wnc = KEf + PEf
The PEf can be dropped from the equation since the skier finishes on the ground at zero height. The KEi can also be dropped since the skier starts from rest. The Wnc term is dropped since it is said that no work is done by non-conservative (external) forces. The equation simplifies to
PEi = KEf
The expressions for KE (0.5*m*v2) and PE (m*g*h) can be substituted into the equation:
m*g*h = 0.5*m*vf2
where m=65.8 kg, h=521 m, g=9.8 m/s/s. Substituting and solving for vf yields 101 m/s.
b. This equation can be solved in a similar manner, except that now the Wext term is -140000 J. So the equation becomes
m*g*h - 140000 J = 0.5*m*vf2
Now substituting and solving for vf yields 77.2 m/s.
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
33. Use the work-energy theorem to determine the force required to stop a 988-kg car moving at a speed of 21.2 m/s if there is a distance of 45.7 m in which to stop it. PSYW
|
Answer: F = 4.86*103 N
The work energy theorem can be written as
KEi + PEi + Wnc = KEf + PEf
The PEi and PEf can be dropped from the equation since they are both 0 (the height of the car is 0 m). The KEf can also be dropped for the same reason (the car is finally stopped). The equation simplifies to
KEi + Wnc = 0
The expressions for KE (0.5*m*v2) and Wnc (F*d*cos[Theta]) can be substituted into the equation:
0.5*m*vi2 + F*d*cos[Theta] = 0
where m=988 kg, vi=21.2 m/s, d=45.7 m, and Theta = 180 degrees. Substituting and solving for F yields 4.86*103 N.
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
Part C: Work-Energy Bar Charts, Analysis, and Conceptual Reasoning
34. Consider the following physical situations. Identify the forces which do work upon the indicated object (in boldface type) and categorize them as conservative or non-conservative forces. Then indicate whether the total mechanical energy of the object changes; it it changes, then indicate whether the change is a positive or negative change. Finally, indicate whether the potential energy and the kinetic energy changes; if PE or KE changes, then indicate whether the change is a positive or negative change.
Description of Physical Situation
|
Identity of Forces
Which Do Work:
|
Change in TME
|
Change in PE
|
Change in KE
|
Conserv-
ative
|
Non-
Conserv-
ative
|
Yes
(+ or -)
|
No
|
Yes
(+ or -)
|
No
|
Yes
(+ or -)
|
No
|
|
a. A force is applied to move a physics cart from the floor to the top of an inclined plane at a constant speed.
|
Gravity
|
Applied
|
+
|
|
+
|
|
|
No
|
|
b. A physics student scurries up a flight of stairs at constant speed.
|
Gravity
|
Applied or Normal
|
+
|
|
+
|
|
|
No
|
|
c. In a moment of unsupervised phun, a physics student hoists herself onto a staircase banister and accelerates down the banister. Ignore all friction forces.
|
Gravity
|
None
|
|
No
|
-
|
|
+
|
|
|
d. A ball is dropped from rest from on the top of a hill and falls to the ground below. Ignore air resistance.
|
Gravity
|
None
|
|
No
|
-
|
|
+
|
|
|
e. A ball leaves top of a hill with a large horizontal velocity. It falls to the ground below. Ignore air resistance.
|
Gravity
|
None
|
|
No
|
-
|
|
+
|
|
|
f. A Hot Wheels car is at rest at an elevated position along an inclined plane; it is released and rolls to a position along the ground. Ignore air resistance.
|
Gravity
|
None
|
|
No
|
-
|
|
+
|
|
|
g. A Hot Wheels car is in motion at the bottom of a hill when it hits a computer diskette box and skids to a stop.
|
None
|
Applied
|
-
|
|
|
No
|
-
|
|
|
h. A pendulum bob swings from its highest position to its lowest position.
|
Gravity
|
None
|
|
No
|
-
|
|
+
|
|
|
i. A physics cart is released from rest at an elevated position along an inclined plane; it is released and rolls to a position along the incline approximately 5 cm from the bottom.
|
Gravity
|
None
|
|
No
|
-
|
|
+
|
|
|
Answer: See table above
Note that whenever a non-conservative force is doing work (as in a, b, g), the total mechanical energy is changing.
However, when the only forces which do work are conservative forces, the total mechanical energy will remaining constant (i.e., be conserved). In such cases, energy will change form from potential to kinetic energy (or vice versa); yet the total amount of the two forms would not be changed.
Potential energy can be considered to change if an object changes its height; if the height decreases, then the potential energy decreases; it the height increases, then the potential energy increases.
Kinetic energy can be considered to change if an object changes its speed; if the speed decreases, then the kinetic energy decreases; it the speed increases, then the kinetic energy increases.
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
35. The diagrams below depict a physical situation. Analyze each situation and construct work-energy bar charts.
|
Answer: See above table; explanations given below.
There are a couple of major principles behind these bar charts: First, the initial energy (KEi + PEgi + PEsi) plus the work done by non-conservative forces (Wnc) must equal the final energy (KEf + PEgf + PEsf); thus the heights of the bars on the left side of the chart must equal the height of the bars on the left side of the chart. Second, the bars must appropriately depict the form of energy and the relative amount for both the initial and final state. The above charts are not the only means of appropriately representing the motion. Other renditions which adhere to these two basic principles would be considered correct.
a. The car is initially at rest (no KE) and has some height above the floor (there is PEg). The car is moving at the bottom of the track (there is KE) but it does not have any height (no PEg). Since there is no friction nor air resistance, the Wnc term is zero.
b. Part b is similar to part a with the exception that friction and air resistance are to be considered in part b. So the analysis involves a consideration of the Wnc term. The Wnc term is negative since friction and air resistance are forces which oppose the motion of an object. The result is that energy has been removed from the system and the final kinetic energy bar is less than the initial potential energy bar.
c. If the tabletop (or floor) is considered the zero level, then the bob has gravitational potential energy in both its initial and final states. Yet the final PEg is less than the initial PEg since the final height (as shown) is less than the initial height. Since the air resistance is negligible, the Wnc term is zero. The difference in potential energy must be made up for in the form of kinetic energy. The bob would still be moving at the final position as shown.
d. This analysis is identical to part a except that the car has been replaced by a ball.
e. The dart is initially above the ground (the assumed zero-level) and finishes above the ground but a little lower than the initial height; thus, there is some PEg to begin with and a little less PEg in the final state. The springs are initially compressed, so there is some initial PEs. The wall does work upon the dart to stop it; this would be negative work since the force is exerted in a direction opposite the motion of the dart. Initially the dart is not moving; so there is no initial KE. And after hitting the wall, it is not moving as well.
f. The worker is applying a force to displace the crate; this is a non-conservative force and so there will be a Wnc term. Since this applied force is in the direction of motion, the Wnc term will be positive. The crate is moving (it has KE) at a constant speed; since the speed is constant, the amount of KE is the same in the initial state as in the final state. Initially there is no gravitational potential energy (PEg) since the crate starts on the ground; in the final state, there is some gravitational potential energy (PEg) since the crate is at an elevated position.
|
36. Several physical situations are described below. For each situation, simplify the work-energy equation by canceling any zero terms and any energy terms (whether KE or PE) which are unchanging. Explain each term which gets canceled. The first problem is done as an example.
|
Description of Physical Situation
|
Simplification of Work-Energy Equation
|
|
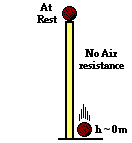 a. A ball starts from rest on top of a tall pillar and falls to the ground below. Assume the effect of air resistance is negligible. a. A ball starts from rest on top of a tall pillar and falls to the ground below. Assume the effect of air resistance is negligible.
|
PEi = KEf
(Since initially at rest, KEi = 0 and cancels. Since the final height is 0, PEf = 0 and cancels. Since non-conservative forces are not doing work, Wnc = 0)
|
|
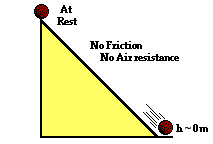 b. A ball starts from rest at an elevated position along an inclined plane and rolls to the ground below. Assume that the effect of friction and air resistance is negligible. b. A ball starts from rest at an elevated position along an inclined plane and rolls to the ground below. Assume that the effect of friction and air resistance is negligible.
|
PEi = KEf
(Initially the ball is at rest, KEi = 0 and cancels. Since the final height is 0, PEf = 0 and cancels. Since non-conservative forces are not doing work, Wnc
|
|
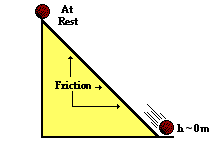 c. A ball starts from rest at an elevated position along an inclined plane and rolls to the ground below. Consider the effect of friction and air resistance. c. A ball starts from rest at an elevated position along an inclined plane and rolls to the ground below. Consider the effect of friction and air resistance.
|
PEi + Wnc = KEf
(Initially the ball is at rest, KEi = 0 and cancels. Since the final height is 0, PEf = 0 and cancels. Friction is a non-conservative forces and it does work so Wnc does not cancel.)
|
|
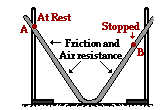 d. A track is constructed by stretching a grooved and pliable material between two lab poles. A metal ball starts from rest at point A and rolls to point B. Friction and air resistance have an effect upon the ball's motion. d. A track is constructed by stretching a grooved and pliable material between two lab poles. A metal ball starts from rest at point A and rolls to point B. Friction and air resistance have an effect upon the ball's motion.
|
PEi + Wnc = PEf
(The ball is at rest in both its initial and final states, so both KEi = 0 and KEf = 0 and cancels. Friction and air resistance are non-conservative forces and do work so Wnc does not cancel.)
|
|
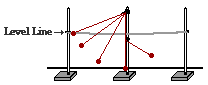 e. A pendulum bob is mounted on top of a lab pole and drawn back to a string which it tied between two other poles. The pendulum bob is released from rest. Upon reaching the vertical, the string hits a barrier and a new pivot point is established as the bob continues in motion along an upward trajectory. Ignore the effect of air resistance. e. A pendulum bob is mounted on top of a lab pole and drawn back to a string which it tied between two other poles. The pendulum bob is released from rest. Upon reaching the vertical, the string hits a barrier and a new pivot point is established as the bob continues in motion along an upward trajectory. Ignore the effect of air resistance.
|
PEi = KEf + PEf
(Initially the ball is at rest, KEi = 0 and cancels. At the point shown in the diagram as the final state, the ball has both height and would still be moving; so neither final energy term would cancel. The only non-conservative force present - tension - does not do work since it is directed at 90-degrees to the direction of motion; so Wnc cancels.)
|
|
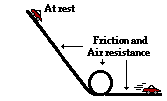 f. A Hot Wheels car starts from rest on top of an inclined plane and rolls down the incline through a loop and along a horizontal surface. Friction and air resistance have a significant effect on the car. f. A Hot Wheels car starts from rest on top of an inclined plane and rolls down the incline through a loop and along a horizontal surface. Friction and air resistance have a significant effect on the car.
|
PEi + Wnc = KEf
(Initially the car is at rest, KEi = 0 and cancels. Since the final height is 0, PEf = 0 and cancels. Friction is a non-conservative forces and it does work so Wnc does not cancel.)
|
|
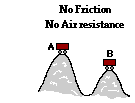 g. An unattended hot dog wagon starts from rest and rolls down a hill and up a second hill. Ignore the effect of friction and air resistance. g. An unattended hot dog wagon starts from rest and rolls down a hill and up a second hill. Ignore the effect of friction and air resistance.
|
PEi = KEf + PEf
(Initially the wagon is at rest, KEi = 0 and cancels. The wagon has height in its initial state, so the PEi term does not cancel. At the point shown in the diagram as the final state, the wagon has both height and would still be moving; so neither final energy term would cancel. There is no friction nor air resistance and the normal force does not do work since it is perpendicular to the displacement; so Wnc cancels.)
|
|
 h. A roller coaster car is already in motion on the top of the first drop and rolls along the track over a couple of hills. Ignore the effect of friction and air resistance. h. A roller coaster car is already in motion on the top of the first drop and rolls along the track over a couple of hills. Ignore the effect of friction and air resistance.
|
PEi = KEf + PEf
(Initially the car is at rest, KEi = 0 and cancels. The car has height in its initial state, so the PEi term does not cancel. At the point shown in the diagram as the final state, the car has both height and would still be moving; so neither final energy term would cancel. There is no friction nor air resistance and the normal force does not do work since it is perpendicular to the displacement; so Wnc cancels.)
|
|
 i. A cross-country skier is in motion on top of a small hill. He skis down the hill into the valley and up a second smaller hill. He uses his poles to propel himself during the entire motion. Ignore the effect of friction and air resistance. i. A cross-country skier is in motion on top of a small hill. He skis down the hill into the valley and up a second smaller hill. He uses his poles to propel himself during the entire motion. Ignore the effect of friction and air resistance.
|
KEi + PEi + Wnc = KEf + PEf
(Initially, the skier has height and motion and so neither initial energy term will cancel. The skier is using his poles to propel himself so there is a non-conservative force doing work; the Wnc term does not cancel. In the final state, the skier is moving and has height (presuming that the zero level is the valley) and so neither final energy term will cancel.
|
[ #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 ]
Navigate to:
Review Session Home - Topic Listing
Work and Energy - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-10 || #11-25 || #26-36 || #37-45
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Work and Energy
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 3 of the series includes topics in Work and Energy.
Visit: MOP the App Home || MOP the App - Part 3