 In the early 1600s, Johannes Kepler proposed three laws of planetary motion. Kepler was able to summarize the carefully collected data of his mentor - Tycho Brahe - with three statements that described the motion of planets in a sun-centered solar system. Kepler's efforts to explain the underlying reasons for such motions are no longer accepted; nonetheless, the actual laws themselves are still considered an accurate description of the motion of any planet and any satellite.
In the early 1600s, Johannes Kepler proposed three laws of planetary motion. Kepler was able to summarize the carefully collected data of his mentor - Tycho Brahe - with three statements that described the motion of planets in a sun-centered solar system. Kepler's efforts to explain the underlying reasons for such motions are no longer accepted; nonetheless, the actual laws themselves are still considered an accurate description of the motion of any planet and any satellite.
Kepler's three laws of planetary motion can be described as follows:
- The path of the planets about the sun is elliptical in shape, with the center of the sun being located at one focus. (The Law of Ellipses)
- An imaginary line drawn from the center of the sun to the center of the planet will sweep out equal areas in equal intervals of time. (The Law of Equal Areas)
- The ratio of the squares of the periods of any two planets is equal to the ratio of the cubes of their average distances from the sun. (The Law of Harmonies)
The Law of Ellipses
Kepler's first law - sometimes referred to as the law of ellipses - explains that planets are orbiting the sun in a path described as an ellipse. An ellipse can easily be 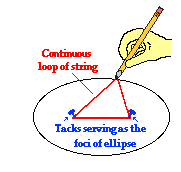 constructed using a pencil, two tacks, a string, a sheet of paper and a piece of cardboard. Tack the sheet of paper to the cardboard using the two tacks. Then tie the string into a loop and wrap the loop around the two tacks. Take your pencil and pull the string until the pencil and two tacks make a triangle (see diagram at the right). Then begin to trace out a path with the pencil, keeping the string wrapped tightly around the tacks. The resulting shape will be an ellipse. An ellipse is a special curve in which the sum of the distances from every point on the curve to two other points is a constant. The two other points (represented here by the tack locations) are known as the foci of the ellipse. The closer together that these points are, the more closely that the ellipse resembles the shape of a circle. In fact, a circle is the special case of an ellipse in which the two foci are at the same location. Kepler's first law is rather simple - all planets orbit the sun in a path that resembles an ellipse, with the sun being located at one of the foci of that ellipse.
constructed using a pencil, two tacks, a string, a sheet of paper and a piece of cardboard. Tack the sheet of paper to the cardboard using the two tacks. Then tie the string into a loop and wrap the loop around the two tacks. Take your pencil and pull the string until the pencil and two tacks make a triangle (see diagram at the right). Then begin to trace out a path with the pencil, keeping the string wrapped tightly around the tacks. The resulting shape will be an ellipse. An ellipse is a special curve in which the sum of the distances from every point on the curve to two other points is a constant. The two other points (represented here by the tack locations) are known as the foci of the ellipse. The closer together that these points are, the more closely that the ellipse resembles the shape of a circle. In fact, a circle is the special case of an ellipse in which the two foci are at the same location. Kepler's first law is rather simple - all planets orbit the sun in a path that resembles an ellipse, with the sun being located at one of the foci of that ellipse.
The Law of Equal Areas
Kepler's second law - sometimes referred to as the law of equal areas - describes the speed at which any given planet will move while orbiting the sun. The speed at which any planet moves through space is constantly changing. A planet moves fastest when it is closest to the sun and slowest when it is furthest from the sun. Yet, if an imaginary line were drawn from the center of the planet to the center of the sun, that line would sweep out the same area in equal periods of time. For instance, if an imaginary line were drawn from the earth to the sun, then the area swept out by the line in every 31-day month would be the same. This is depicted in the diagram below. As can be observed in the diagram, the areas formed when the earth is closest to the sun can be approximated as a wide but short triangle; whereas the areas formed when the earth is farthest from the sun can be approximated as a narrow but long triangle. These areas are the same size. Since the base of these triangles are shortest when the earth is farthest from the sun, the earth would have to be moving more slowly in order for this imaginary area to be the same size as when the earth is closest to the sun.
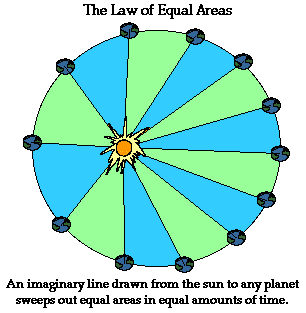

The Law of Harmonies
Kepler's third law - sometimes referred to as the law of harmonies - compares the orbital period and radius of orbit of a planet to those of other planets. Unlike Kepler's first and second laws that describe the motion characteristics of a single planet, the third law makes a comparison between the motion characteristics of different planets. The comparison being made is that the ratio of the squares of the periods to the cubes of their average distances from the sun is the same for every one of the planets. As an illustration, consider the orbital period and average distance from sun (orbital radius) for Earth and mars as given in the table below.
|
Planet
|
Period
(s)
|
Average
Distance (m)
|
T2/R3
(s2/m3)
|
|
Earth
|
3.156 x 107 s
|
1.4957 x 1011
|
2.977 x 10-19
|
|
Mars
|
5.93 x 107 s
|
2.278 x 1011
|
2.975 x 10-19
|
Observe that the T2/R3 ratio is the same for Earth as it is for mars. In fact, if the same T2/R3 ratio is computed for the other planets, it can be found that this ratio is nearly the same value for all the planets (see table below). Amazingly, every planet has the same T2/R3 ratio.
|
Planet
|
Period
(yr)
|
Average
Distance (au)
|
T2/R3
(yr2/au3)
|
|
Mercury
|
0.241
|
0.39
|
0.98
|
|
Venus
|
.615
|
0.72
|
1.01
|
|
Earth
|
1.00
|
1.00
|
1.00
|
|
Mars
|
1.88
|
1.52
|
1.01
|
|
Jupiter
|
11.8
|
5.20
|
0.99
|
|
Saturn
|
29.5
|
9.54
|
1.00
|
|
Uranus
|
84.0
|
19.18
|
1.00
|
|
Neptune
|
165
|
30.06
|
1.00
|
|
Pluto
|
248
|
39.44
|
1.00
|
(NOTE: The average distance value is given in astronomical units where 1 a.u. is equal to the distance from the earth to the sun - 1.4957 x 1011 m. The orbital period is given in units of earth-years where 1 earth year is the time required for the earth to orbit the sun - 3.156 x 107 seconds. )
Kepler's third law provides an accurate description of the period and distance for a planet's orbits about the sun. Additionally, the same law that describes the T2/R3 ratio for the planets' orbits about the sun also accurately describes the T2/R3 ratio for any satellite (whether a moon or a man-made satellite) about any planet. There is something much deeper to be found in this T2/R3 ratio - something that must relate to basic fundamental principles of motion. In the next part of Lesson 4, these principles will be investigated as we draw a connection between the circular motion principles discussed in Lesson 1 and the motion of a satellite.
How did Newton Extend His Notion of Gravity to Explain Planetary Motion?
Newton's comparison of the acceleration of the moon to the acceleration of objects on earth allowed him to establish that the moon is held in a circular orbit by the force of gravity - a force that is inversely dependent upon the distance between the two objects' centers. Establishing gravity as the cause of the moon's orbit does not necessarily establish that gravity is the cause of the planet's orbits. How then did Newton provide credible evidence that the force of gravity is meets the centripetal force requirement for the elliptical motion of planets?
Recall from earlier in Lesson 3 that Johannes Kepler proposed three laws of planetary motion. His Law of Harmonies suggested that the ratio of the period of orbit squared (T2) to the mean radius of orbit cubed (R3) is the same value k for all the planets that orbit the sun. Known data for the orbiting planets suggested the following average ratio:
k = 2.97 x 10-19 s2/m3 = (T2)/(R3)
Newton was able to combine the law of universal gravitation with circular motion principles to show that if the force of gravity provides the centripetal force for the planets' nearly circular orbits, then a value of 2.97 x 10-19 s2/m3 could be predicted for the T2/R3 ratio. Here is the reasoning employed by Newton:
Consider a planet with mass Mplanet to orbit in nearly circular motion about the sun of mass MSun. The net centripetal force acting upon this orbiting planet is given by the relationship
Fnet = (Mplanet * v2) / R
This net centripetal force is the result of the gravitational force that attracts the planet towards the sun, and can be represented as
Fgrav = (G* Mplanet * MSun ) / R2
Since Fgrav = Fnet, the above expressions for centripetal force and gravitational force are equal. Thus,
(Mplanet * v2) / R = (G* Mplanet * MSun ) / R2
Since the velocity of an object in nearly circular orbit can be approximated as v = (2*pi*R) / T,
v2 = (4 * pi2 * R2) / T2
Substitution of the expression for v2 into the equation above yields,
(Mplanet * 4 * pi2 * R2) / (R • T2) = (G* Mplanet * MSun ) / R2
By cross-multiplication and simplification, the equation can be transformed into
T2 / R3 = (Mplanet * 4 * pi2) / (G* Mplanet * MSun )
The mass of the planet can then be canceled from the numerator and the denominator of the equation's right-side, yielding
T2 / R3 = (4 * pi2) / (G * MSun )
The right side of the above equation will be the same value for every planet regardless of the planet's mass. Subsequently, it is reasonable that the T2/R3 ratio would be the same value for all planets if the force that holds the planets in their orbits is the force of gravity. Newton's universal law of gravitation predicts results that were consistent with known planetary data and provided a theoretical explanation for Kepler's Law of Harmonies.
Scientists know much more about the planets than they did in Kepler's days. Use The Planets widget bleow to explore what is known of the various planets.
Check Your Understanding
1. Our understanding of the elliptical motion of planets about the Sun spanned several years and included contributions from many scientists.
a. Which scientist is credited with the collection of the data necessary to support the planet's elliptical motion?
b. Which scientist is credited with the long and difficult task of analyzing the data?
c. Which scientist is credited with the accurate explanation of the data?
2. Galileo is often credited with the early discovery of four of Jupiter's many moons. The moons orbiting Jupiter follow the same laws of motion as the planets orbiting the sun. One of the moons is called Io - its distance from Jupiter's center is 4.2 units and it orbits Jupiter in 1.8 Earth-days. Another moon is called Ganymede; it is 10.7 units from Jupiter's center. Make a prediction of the period of Ganymede using Kepler's law of harmonies.
3. Suppose a small planet is discovered that is 14 times as far from the sun as the Earth's distance is from the sun (1.5 x 1011 m). Use Kepler's law of harmonies to predict the orbital period of such a planet. GIVEN: T2/R3 = 2.97 x 10-19 s2/m3
4. The average orbital distance of Mars is 1.52 times the average orbital distance of the Earth. Knowing that the Earth orbits the sun in approximately 365 days, use Kepler's law of harmonies to predict the time for Mars to orbit the sun.
Orbital radius and orbital period data for the four biggest moons of Jupiter are listed in the table below. The mass of the planet Jupiter is 1.9 x 1027 kg. Base your answers to the next five questions on this information.
|
Jupiter's Moon
|
Period (s)
|
Radius (m)
|
T2/R3
|
|
Io
|
1.53 x 105
|
4.2 x 108
|
a.
|
|
Europa
|
3.07 x 105
|
6.7 x 108
|
b.
|
|
Ganymede
|
6.18 x 105
|
1.1 x 109
|
c.
|
|
Callisto
|
1.44 x 106
|
1.9 x 109
|
d.
|
5. Determine the T2/R3 ratio (last column) for Jupiter's moons.
6. What pattern do you observe in the last column of data? Which law of Kepler's does this seem to support?
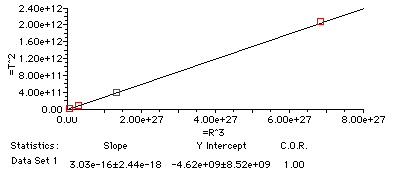
7. Use the graphing capabilities of your TI calculator to plot T2 vs. R3 (T2 should be plotted along the vertical axis) and to determine the equation of the line. Write the equation in slope-intercept form below.
See graph below.
8. How does the T2/R3 ratio for Jupiter (as shown in the last column of the data table) compare to the T2/R3 ratio found in #7 (i.e., the slope of the line)?
9. How does the T2/R3 ratio for Jupiter (as shown in the last column of the data table) compare to the T2/R3 ratio found using the following equation? (G=6.67x10-11 N*m2/kg2 and MJupiter = 1.9 x 1027 kg)
T2 / R3 = (4 * pi2) / (G * MJupiter )
Graph for Question #6
Return to Question #6