Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 The final mathematical quantity discussed in Lesson 1 is acceleration. An often confused quantity, acceleration has a meaning much different than the meaning associated with it by sports announcers and other individuals. The definition of acceleration is:
The final mathematical quantity discussed in Lesson 1 is acceleration. An often confused quantity, acceleration has a meaning much different than the meaning associated with it by sports announcers and other individuals. The definition of acceleration is:
- Acceleration is a vector quantity that is defined as the rate at which an object changes its velocity. An object is accelerating if it is changing its velocity.
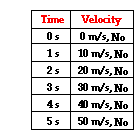 Sports announcers will occasionally say that a person is accelerating if he/she is moving fast. Yet acceleration has nothing to do with going fast. A person can be moving very fast and still not be accelerating. Acceleration has to do with changing how fast an object is moving. If an object is not changing its velocity, then the object is not accelerating. The data at the right are representative of a northward-moving accelerating object. The velocity is changing over the course of time. In fact, the velocity is changing by a constant amount - 10 m/s - in each second of time. Anytime an object's velocity is changing, the object is said to be accelerating; it has an acceleration.
Sports announcers will occasionally say that a person is accelerating if he/she is moving fast. Yet acceleration has nothing to do with going fast. A person can be moving very fast and still not be accelerating. Acceleration has to do with changing how fast an object is moving. If an object is not changing its velocity, then the object is not accelerating. The data at the right are representative of a northward-moving accelerating object. The velocity is changing over the course of time. In fact, the velocity is changing by a constant amount - 10 m/s - in each second of time. Anytime an object's velocity is changing, the object is said to be accelerating; it has an acceleration.
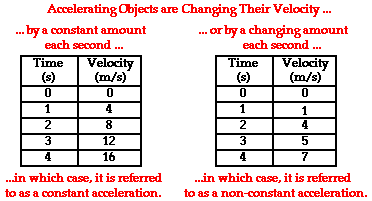
The Meaning of Constant Acceleration
Sometimes an accelerating object will change its velocity by the same amount each second. As mentioned in the previous paragraph, the data table above show an object changing its velocity by 10 m/s in each consecutive second. This is referred to as a constant acceleration since the velocity is changing by a constant amount each second. An object with a constant acceleration should not be confused with an object with a constant velocity. Don't be fooled! If an object is changing its velocity -whether by a constant amount or a varying amount - then it is an accelerating object. And an object with a constant velocity is not accelerating. The data tables below depict motions of objects with a constant acceleration and a changing acceleration. Note that each object has a changing velocity.
Since accelerating objects are constantly changing their velocity, one can say that the distance traveled/time is not a constant value. A falling object for instance usually accelerates as it falls. If we were to observe the motion of a free-falling object (free fall motion will be discussed in detail later), we would observe that the object averages a velocity of approximately 5 m/s in the first second, approximately 15 m/s in the second second, approximately 25 m/s in the third second, approximately 35 m/s in the fourth second, etc. Our free-falling object would be constantly accelerating. Given these average velocity values during each consecutive 1-second time interval, we could say that the object would fall 5 meters in the first second, 15 meters in the second second (for a total distance of 20 meters), 25 meters in the third second (for a total distance of 45 meters), 35 meters in the fourth second (for a total distance of 80 meters after four seconds). These numbers are summarized in the table below.
Time
Interval |
Velocity Change
During Interval |
Ave. Velocity
During Interval |
Distance Traveled
During Interval |
Total Distance Traveled from
0 s to End of Interval |
| 0 – 1.0 s |
0 to ~10 m/s |
~5 m/s |
~5 m |
~5 m |
| 1.0 – 2.0 s |
~10 to 20 m/s |
~15 m/s |
~15 m |
~20 m |
| 2.0 – 3.0 s |
~20 to 30 m/s |
~25 m/s |
~25 m |
~45 m |
| 3.0 – 4.0 s |
~30 to 40 m/s |
~35 m/s |
~35 m |
~80 m |
Note: The ~ symbol as used here means approximately.
This discussion illustrates that a free-falling object that is accelerating at a constant rate will cover different distances in each consecutive second. Further analysis of the first and last columns of the data above reveal that there is a square relationship between the total distance traveled and the time of travel for an object starting from rest and moving with a constant acceleration. The total distance traveled is directly proportional to the square of the time. As such, if an object travels for twice the time, it will cover four times (2^2) the distance; the total distance traveled after two seconds is four times the total distance traveled after one second. If an object travels for three times the time, then it will cover nine times (3^2) the distance; the distance traveled after three seconds is nine times the distance traveled after one second. Finally, if an object travels for four times the time, then it will cover 16 times (4^2) the distance; the distance traveled after four seconds is 16 times the distance traveled after one second. For objects with a constant acceleration, the distance of travel is directly proportional to the square of the time of travel.
Calculating the Average Acceleration
The average acceleration (a) of any object over a given interval of time (t) can be calculated using the equation
This equation can be used to calculate the acceleration of the object whose motion is depicted by the velocity-time data table above. The velocity-time data in the table shows that the object has an acceleration of 10 m/s/s. The calculation is shown below.
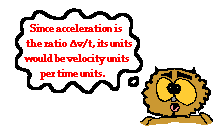 Acceleration values are expressed in units of velocity/time. Typical acceleration units include the following:
Acceleration values are expressed in units of velocity/time. Typical acceleration units include the following:
m/s/s
mi/hr/s
km/hr/s
m/s2
These units may seem a little awkward to a beginning physics student. Yet they are very reasonable units when you begin to consider the definition and equation for acceleration. The reason for the units becomes obvious upon examination of the acceleration equation.
Since acceleration is a velocity change over a time, the units on acceleration are velocity units divided by time units - thus (m/s)/s or (mi/hr)/s. The (m/s)/s unit can be mathematically simplified to m/s2.
The Direction of the Acceleration Vector
Since acceleration is a vector quantity, it has a direction associated with it. The direction of the acceleration vector depends on two things:
- whether the object is speeding up or slowing down
- whether the object is moving in the + or - direction
 The general principle for determining the acceleation is:
The general principle for determining the acceleation is:
If an object is slowing down, then its acceleration is in the opposite direction of its motion.
This general principle can be applied to determine whether the sign of the acceleration of an object is positive or negative, right or left, up or down, etc. Consider the two data tables below. In each case, the acceleration of the object is in the positive direction. In Example A, the object is moving in the positive direction (i.e., has a positive velocity) and is speeding up. When an object is speeding up, the acceleration is in the same direction as the velocity. Thus, this object has a positive acceleration. In Example B, the object is moving in the negative direction (i.e., has a negative velocity) and is slowing down. According to our general principle, when an object is slowing down, the acceleration is in the opposite direction as the velocity. Thus, this object also has a positive acceleration.

This same general principle can be applied to the motion of the objects represented in the two data tables below. In each case, the acceleration of the object is in the negative direction. In Example C, the object is moving in the positive direction (i.e., has a positive velocity) and is slowing down. According to our principle, when an object is slowing down, the acceleration is in the opposite direction as the velocity. Thus, this object has a negative acceleration. In Example D, the object is moving in the negative direction (i.e., has a negative velocity) and is speeding up. When an object is speeding up, the acceleration is in the same direction as the velocity. Thus, this object also has a negative acceleration.
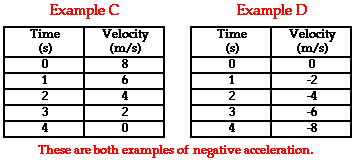

Observe the use of positive and negative as used in the discussion above (Examples A - D). In physics, the use of positive and negative always has a physical meaning. It is more than a mere mathematical symbol. As used here to describe the velocity and the acceleration of a moving object, positive and negative describe a direction. Both velocity and acceleration are vector quantities and a full description of the quantity demands the use of a directional adjective. North, south, east, west, right, left, up and down are all directional adjectives. Physics often borrows from mathematics and uses the + and - symbols as directional adjectives. Consistent with the mathematical convention used on number lines and graphs, positive often means to the right or up and negative often means to the left or down. So to say that an object has a negative acceleration as in Examples C and D is to simply say that its acceleration is to the left or down (or in whatever direction has been defined as negative). Negative accelerations do not refer acceleration values that are less than 0. An acceleration of -2 m/s/s is an acceleration with a magnitude of 2 m/s/s that is directed in the negative direction.
We Would Like to Suggest ...
 Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our Name That Motion Interactive. It is found in the Physics Interactive section and allows a learner to apply concepts of speed, velocity and acceleration.
Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our Name That Motion Interactive. It is found in the Physics Interactive section and allows a learner to apply concepts of speed, velocity and acceleration.
Check Your Understanding
To test your understanding of the concept of acceleration, consider the following problems and the corresponding solutions. Use the equation for acceleration to determine the acceleration for the following two motions.