Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 As mentioned earlier in this lesson, an object moving in a circle is experiencing an acceleration. Even if moving around the perimeter of the circle with a constant speed, there is still a change in velocity and subsequently an acceleration. This acceleration is directed towards the center of the circle. And in accord with Newton's second law of motion, an object which experiences an acceleration must also be experiencing a net force. The direction of the net force is in the same direction as the acceleration. So for an object moving in a circle, there must be an inward force acting upon it in order to cause its inward acceleration. This is sometimes referred to as the centripetal force requirement. The word centripetal (not to be confused with the F-word centrifugal) means center seeking. For object's moving in circular motion, there is a net force acting towards the center which causes the object to seek the center.
As mentioned earlier in this lesson, an object moving in a circle is experiencing an acceleration. Even if moving around the perimeter of the circle with a constant speed, there is still a change in velocity and subsequently an acceleration. This acceleration is directed towards the center of the circle. And in accord with Newton's second law of motion, an object which experiences an acceleration must also be experiencing a net force. The direction of the net force is in the same direction as the acceleration. So for an object moving in a circle, there must be an inward force acting upon it in order to cause its inward acceleration. This is sometimes referred to as the centripetal force requirement. The word centripetal (not to be confused with the F-word centrifugal) means center seeking. For object's moving in circular motion, there is a net force acting towards the center which causes the object to seek the center.
To understand the importance of a centripetal force, it is important to have a sturdy understanding of the Newton's first law of motion - the law of inertia. The law of inertia states that ...
|
... objects in motion tend to stay in motion with the same speed and the same direction unless acted upon by an unbalanced force.
|
According to Newton's first law of motion, it is the natural tendency of all moving objects to continue in motion in the same direction that they are moving ... unless some form of unbalanced force acts upon the object to deviate its motion from its straight-line path. Moving objects will tend to naturally travel in straight lines; an unbalanced force is only required to cause it to turn. Thus, the presence of an unbalanced force is required for objects to move in circles.
Inertia, Force and Acceleration for an Automobile Passenger
The idea expressed by Newton's law of inertia should not be surprising to us. We experience this phenomenon of inertia nearly everyday when we drive our automobile. For example, imagine that you are a passenger in a car at a traffic light. The light turns green and the driver accelerates from rest. The car begins to accelerate forward, yet relative to the seat which you are on your body begins to lean backwards. Your body being at rest tends to stay at rest. This is one aspect of the law of inertia - "objects at rest tend to stay at rest." As the wheels of the car spin to generate a forward force upon the car and cause a forward acceleration, your body tends to stay in place. It certainly might seem to you as though your body were experiencing a backwards force causing it to accelerate backwards. Yet you would have a difficult time identifying such a backwards force on your body. Indeed there isn't one. The feeling of being thrown backwards is merely the tendency of your body to resist the acceleration and to remain in its state of rest. The car is accelerating out from under your body, leaving you with the false feeling of being pushed backwards.
Now imagine that you are in the same car moving along at a constant speed approaching a stoplight. The driver applies the brakes, the wheels of the car lock, and the car begins to skid to a stop. There is a backwards force upon the forward moving car and subsequently a backwards acceleration on the car. However, your body, being in motion, tends to continue in motion while the car is skidding to a stop. It certainly might seem to you as though your body were experiencing a forwards force causing it to accelerate forwards. Yet you would once more have a difficult time identifying such a forwards force on your body. Indeed there is no physical object accelerating you forwards. The feeling of being thrown forwards is merely the tendency of your body to resist the deceleration and to remain in its state of forward motion. This is the second aspect of Newton's law of inertia - "an object in motion tends to stay in motion with the same speed and in the same direction... ." The unbalanced force acting upon the car causes the car to slow down while your body continues in its forward motion. You are once more left with the false feeling of being pushed in a direction which is opposite your acceleration.
These two driving scenarios are summarized by the following graphic.
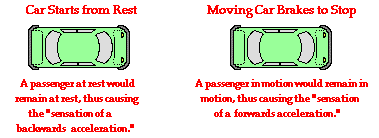
In each case - the car starting from rest and the moving car braking to a stop - the direction which the passengers lean is opposite the direction of the acceleration. This is merely the result of the passenger's inertia - the tendency to resist acceleration. The passenger's lean is not an acceleration in itself but rather the tendency to maintain the state of motion while the car does the acceleration. The tendency of a passenger's body to maintain its state of rest or motion while the surroundings (the car) accelerate is often misconstrued as an acceleration. This becomes particularly problematic when we consider the third possible inertia experience of a passenger in a moving automobile - the left hand turn.
Suppose that on the next part of your travels the driver of the car makes a sharp turn to the left at constant speed. During the turn, the car travels in a circular-type path. That is, the car 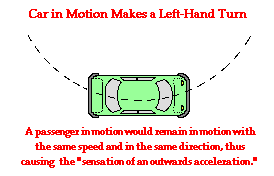 sweeps out one-quarter of a circle. The friction force acting upon the turned wheels of the car causes an unbalanced force upon the car and a subsequent acceleration. The unbalanced force and the acceleration are both directed towards the center of the circle about which the car is turning. Your body however is in motion and tends to stay in motion. It is the inertia of your body - the tendency to resist acceleration - that causes it to continue in its forward motion. While the car is accelerating inward, you continue in a straight line. If you are sitting on the passenger side of the car, then eventually the outside door of the car will hit you as the car turns inward. This phenomenon might cause you to think that you are being accelerated outwards away from the center of the circle. In reality, you are continuing in your straight-line inertial path tangent to the circle while the car is accelerating out from under you. The sensation of an outward force and an outward acceleration is a false sensation. There is no physical object capable of pushing you outwards. You are merely experiencing the tendency of your body to continue in its path tangent to the circular path along which the car is turning. You are once more left with the false feeling of being pushed in a direction that is opposite your acceleration.
sweeps out one-quarter of a circle. The friction force acting upon the turned wheels of the car causes an unbalanced force upon the car and a subsequent acceleration. The unbalanced force and the acceleration are both directed towards the center of the circle about which the car is turning. Your body however is in motion and tends to stay in motion. It is the inertia of your body - the tendency to resist acceleration - that causes it to continue in its forward motion. While the car is accelerating inward, you continue in a straight line. If you are sitting on the passenger side of the car, then eventually the outside door of the car will hit you as the car turns inward. This phenomenon might cause you to think that you are being accelerated outwards away from the center of the circle. In reality, you are continuing in your straight-line inertial path tangent to the circle while the car is accelerating out from under you. The sensation of an outward force and an outward acceleration is a false sensation. There is no physical object capable of pushing you outwards. You are merely experiencing the tendency of your body to continue in its path tangent to the circular path along which the car is turning. You are once more left with the false feeling of being pushed in a direction that is opposite your acceleration.

The Centripetal Force and Direction Change
Any object moving in a circle (or along a circular path) experiences a centripetal force. That is, there is some physical force pushing or pulling the object towards the center of the circle. This is the centripetal force requirement. The word centripetal is merely an adjective used to describe the direction of the force. We are not introducing a new type of force but rather describing the direction of the net force acting upon the object that moves in the circle. Whatever the object, if it moves in a circle, there is some force acting upon it to cause it to deviate from its straight-line path, accelerate inwards and move along a circular path. Three such examples of centripetal force are shown below.
|

|
|

|
|
As a car makes a turn, the force of friction acting upon the turned wheels of the car provides centripetal force required for circular motion.
|
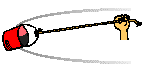
As a bucket of water is tied to a string and spun in a circle, the tension force acting upon the bucket provides the centripetal force required for circular motion.
|
As the moon orbits the Earth, the force of gravity acting upon the moon provides the centripetal force required for circular motion.
|
The centripetal force for uniform circular motion alters the direction of the object without altering its speed. The idea that an unbalanced force can change the direction of the velocity vector but not its magnitude may seem a bit strange. How could that be? There are a number of ways to approach this question. One approach involves to analyze the motion from a work-energy standpoint. Recall from Unit 5 of The Physics Classroom that work is a force acting upon an object to cause a displacement. The amount of work done upon an object is found using the equation
Work = Force * displacement * cosine (Theta)
where the Theta in the equation represents the angle between the force and the displacement. As the centripetal force acts upon an object moving in a circle at constant speed, the force always acts inward as the velocity of the object is directed tangent to the circle. This would mean that the force is always directed perpendicular to the direction that the object is being displaced. The angle Theta in the above equation is 90 degrees and the cosine of 90 degrees is 0. Thus, the work done by the centripetal force in the case of uniform circular motion is 0 Joules. Recall also from Unit 5 of The Physics Classroom that when no work is done upon an object by external forces, the total mechanical energy (potential energy plus kinetic energy) of the object remains constant. So if an object is moving in a horizontal circle at constant speed, the centripetal force does not do work and cannot alter the total mechanical energy of the object. For this reason, the kinetic energy and therefore, the speed of the object will remain constant. The force can indeed accelerate the object - by changing its direction - but it cannot change its speed. In fact, whenever the unbalanced centripetal force acts perpendicular to the direction of motion, the speed of the object will remain constant. For an unbalanced force to change the speed of the object, there would have to be a component of force in the direction of (or the opposite direction of) the motion of the object.
Applying Vector Components and Newton's Second Law
A second approach to this question of why the centripetal force causes a direction change but not a speed change involves vector components and Newton's second law. The following imaginary scenario will be used to help illustrate the point.
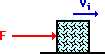
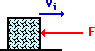
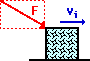
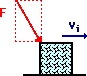
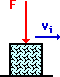
 Suppose at the local ice factory, a block of ice slides out of the freezer and a mechanical arm exerts a force to accelerate it across the icy, friction free surface. Last week, the mechanical arm was malfunctioning and exerting pushes in a randomly directed fashion. The various direction of forces applied to the moving block of ice are shown below. For each case, observe the force in comparison to the direction of motion of the ice block and predict whether the force will speed up, slow down or not affect the speed of the block. Use vector components to make your predictions. Then check your answers by clicking on the button.
Suppose at the local ice factory, a block of ice slides out of the freezer and a mechanical arm exerts a force to accelerate it across the icy, friction free surface. Last week, the mechanical arm was malfunctioning and exerting pushes in a randomly directed fashion. The various direction of forces applied to the moving block of ice are shown below. For each case, observe the force in comparison to the direction of motion of the ice block and predict whether the force will speed up, slow down or not affect the speed of the block. Use vector components to make your predictions. Then check your answers by clicking on the button.
| |
Physical Situation
|
Speed up, slow down or not affect the speed?
|
Explanation
|
|
a.
|
|
|
|
|
b.
|
|
|
|
|
c.
|
|
|
|
|
d.
|
|
|
|
|
e.
|
|
|
|
The examples above illustrate that a force is only capable of slowing down or speeding up an object when there is a component directed in the same direction or opposite direction as the motion of the object. In case e, the vertical force does not alter the horizontal motion. It is sometimes said that perpendicular components of motion are independent of each other. A vertical force cannot affect a horizontal motion.
To summarize, an object in uniform circular motion experiences an inward net force. This inward force is sometimes referred to as a centripetal force, where centripetal describes its direction. Without this centripetal force, an object could never alter its direction. The fact that the centripetal force is directed perpendicular to the tangential velocity means that the force can alter the direction of the object's velocity vector without altering its magnitude.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Uniform Circular Motion Interactive an/or our
Race Track Interactive. You can find these in the Physics Interactives section of our website. Both Interactives allow a learner to interactively explore the net force for an object moving in a circle.
Check Your Understanding
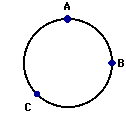 For questions #1-#5: An object is moving in a clockwise direction around a circle at constant speed. Use your understanding of the concepts of velocity, acceleration and force to answer the next five questions. Use the diagram shown at the right. Click the button to check your answers.
For questions #1-#5: An object is moving in a clockwise direction around a circle at constant speed. Use your understanding of the concepts of velocity, acceleration and force to answer the next five questions. Use the diagram shown at the right. Click the button to check your answers.
1. Which vector below represents the direction of the force vector when the object is located at point A on the circle?
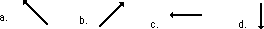
2. Which vector below represents the direction of the force vector when the object is located at point C on the circle?
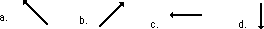
3. Which vector below represents the direction of the velocity vector when the object is located at point B on the circle?
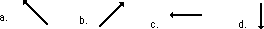
4. Which vector below represents the direction of the velocity vector when the object is located at point C on the circle?
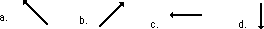
5. Which vector below represents the direction of the acceleration vector when the object is located at point B on the circle?
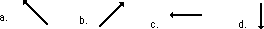
6. Rex Things and Doris Locked are out on a date. Rex makes a rapid right-hand turn. Doris begins sliding across the vinyl seat (that Rex had waxed and polished beforehand) and collides with Rex. To break the awkwardness of the situation, Rex and Doris begin discussing the physics of the motion that was just experienced. Rex suggests that objects which move in a circle experience an outward force. Thus, as the turn was made, Doris experienced an outward force that pushed her towards Rex. Doris disagrees, arguing that objects that move in a circle experience an inward force. In this case, according to Doris, Rex traveled in a circle due to the force of his door pushing him inward. Doris did not travel in a circle since there was no force pushing her inward; she merely continued in a straight line until she collided with Rex. Who is correct? Argue one of these two positions.
7. Kara Lott is practicing winter driving in the GBS parking lot. Kara turns the wheel to make a left-hand turn but her car continues in a straight line across the ice. Teacher A and Teacher B had viewed the phenomenon. Teacher A argues that the lack of a frictional force between the tires and the ice results in a balance of forces that keeps the car traveling in a straight line. Teacher B argues that the ice placed an outward force on the tire to balance the turning force and thus keep the car traveling in a straight line. Which teacher is (A or B) is the physics teacher? ______ Explain the fallacy in the other teacher's argument.