Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 The interaction between charged objects is a non-contact force that acts over some distance of separation. Charge, charge and distance. Every electrical interaction involves a force that highlights the importance of these three variables. Whether it is a plastic golf tube attracting paper bits, two like-charged balloons repelling or a charged Styrofoam plate interacting with electrons in a piece of aluminum, there is always two charges and a distance between them as the three critical variables that influence the strength of the interaction. In this section of Lesson 3, we will explore the importance of these three variables.
The interaction between charged objects is a non-contact force that acts over some distance of separation. Charge, charge and distance. Every electrical interaction involves a force that highlights the importance of these three variables. Whether it is a plastic golf tube attracting paper bits, two like-charged balloons repelling or a charged Styrofoam plate interacting with electrons in a piece of aluminum, there is always two charges and a distance between them as the three critical variables that influence the strength of the interaction. In this section of Lesson 3, we will explore the importance of these three variables.
Force as a Vector Quantity
The electrical force, like all forces, is typically expressed using the unit Newton. Being a force, the strength of the electrical interaction is a vector quantity that has both magnitude and direction. The direction of the electrical force is dependent upon whether the charged objects are charged with like charge or opposite charge and upon their spatial orientation. By knowing the type of charge on the two objects, the direction of the force on either one of them can be determined with a little reasoning. In the diagram below, objects A and B have like charge causing them to repel each other. Thus, the force on object A is directed leftward (away from B) and the force on object B is directed rightward (away from A). On the other hand, objects C and D have opposite charge causing them to attract each other. Thus, the force on object C is directed rightward (toward object D) and the force on object D is directed leftward (toward object C). When it comes to the electrical force vector, perhaps the best way to determine the direction of it is to apply the fundamental rules of charge interaction (opposites attract and likes repel) using a little reasoning.
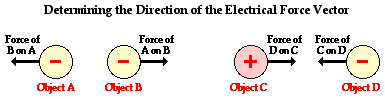
Electrical force also has a magnitude or strength. Like most types of forces, there are a variety of factors that influence the magnitude of the electrical force. Two like-charged balloons will repel each other and the strength of their repulsive force can be altered by changing three variables. First, the quantity of charge on one of the balloons will affect the strength of the repulsive force. The more charged a balloon is, the greater the repulsive force. Second, the quantity of charge on the second balloon will affect the strength of the repulsive force. Gently rub two balloons with animal fur and they repel a little. Rub the two balloons vigorously to impart more charge to both of them, and they repel a lot. Finally, the distance between the two balloons will have a significant and noticeable effect upon the repulsive force. The electrical force is strongest when the balloons are closest together. Decreasing the separation distance increases the force. The magnitude of the force and the distance between the two balloons is said to be inversely related.
Coulomb's Law Equation
The quantitative expression for the effect of these three variables on electric force is known as Coulomb's law. Coulomb's law states that the electrical force between two charged objects is directly proportional to the product of the quantity of charge on the objects and inversely proportional to the square of the separation distance between the two objects. In equation form, Coulomb's law can be stated as

where Q1 represents the quantity of charge on object 1 (in Coulombs), Q2 represents the quantity of charge on object 2 (in Coulombs), and d represents the distance of separation between the two objects (in meters). The symbol k is a proportionality constant known as the Coulomb's law constant. The value of this constant is dependent upon the medium that the charged objects are immersed in. In the case of air, the value is approximately 9.0 x 109 N • m2 / C2. If the charged objects are present in water, the value of k can be reduced by as much as a factor of 80. It is worthwhile to point out that the units on k are such that when substituted into the equation the units on charge (Coulombs) and the units on distance (meters) will be canceled, leaving a Newton as the unit of force.
The Coulomb's law equation provides an accurate description of the force between two objects whenever the objects act as point charges. A charged conducting sphere interacts with other charged objects as though all of its charge were located at its center. While the charge is uniformly spread across the surface of the sphere, the center of charge can be considered to be the center of the sphere. The sphere acts as a point charge with its excess charge located at its center. Since Coulomb's law applies to point charges, the distance d in the equation is the distance between the centers of charge for both objects (not the distance between their nearest surfaces).
The symbols Q1 and Q2 in the Coulomb's law equation represent the quantities of charge on the two interacting objects. Since an object can be charged positively or negatively, these quantities are often expressed as "+" or "-" values. The sign on the charge is simply representative of whether the object has an excess of electrons (a negatively charged object) or a shortage of electrons (a positively charged object). It might be tempting to utilize the "+" and "-" signs in the calculations of force. While the practice is not recommended, there is certainly no harm in doing so. When using the "+" and "-" signs in the calculation of force, the result will be that a "-" value for force is a sign of an attractive force and a "+" value for force signifies a repulsive force. Mathematically, the force value would be found to be positive when Q1 and Q2 are of like charge - either both "+" or both "-". And the force value would be found to be negative when Q1 and Q2 are of opposite charge - one is "+" and the other is "-". This is consistent with the concept that oppositely charged objects have an attractive interaction and like charged objects have a repulsive interaction. In the end, if you're thinking conceptually (and not merely mathematically), you would be very able to determine the nature of the force - attractive or repulsive - without the use of "+" and "-" signs in the equation.
Calculations Using Coulomb's Law
In physics courses, Coulomb's law is often used as a type of algebraic recipe to solve physics word problems. Three such examples are shown here.
|
Example A
Suppose that two point charges, each with a charge of +1.00 Coulomb are separated by a distance of 1.00 meter. Determine the magnitude of the electrical force of repulsion between them.
|
This is not the most difficult mathematical problem that could be selected. It certainly was not chosen for its mathematical rigor. The problem-solving strategy utilized here may seem unnecessary given the simplicity of the given values. Nonetheless, the strategy will be used to illustrate its usefulness to any Coulomb's law problem.
The first step of the strategy is the identification and listing of known information in variable form. Here we know the charges of the two objects (Q1 and Q2) and the separation distance between them (d). The next step of the strategy involves the listing of the unknown (or desired) information in variable form. In this case, the problem requests information about the force. So Felect is the unknown quantity. The results of the first two steps are shown in the table below.
|
Given:
Q1 = 1.00 C
Q2 = 1.00 C
d = 1.00 m
|
Find:
Felect = ???
|
The next and final step of the strategy involves substituting known values into the Coulomb's law equation and using proper algebraic steps to solve for the unknown information. This step is shown below.
Felect = k • Q1 • Q2 / d2
Felect = (9.0 x 109 N•m2/C2) • (1.00 C) • (1.00 C) / (1.00 m)2
Felect = 9.0 x 109 N
The force of repulsion of two +1.00 Coulomb charges held 1.00 meter apart is 9 billion Newton. This is an incredibly large force that compares in magnitude to the weight of more than 2000 jetliners.
This problem was chosen primarily for its conceptual message. Objects simply do not acquire charges on the order of 1.00 Coulomb. In fact, more likely Q values are on the order of 10-9 or possibly 10-6 Coulombs. For this reason, a Greek prefix is often used in front of the Coulomb as a unit of charge. Charge is often expressed in units of microCoulomb (µC) and nanoCoulomb (nC). If a problem states the charge in these units, it is advisable to first convert to Coulombs prior to substitution into the Coulomb's law equation. The following unit equivalencies will assist in such conversions.
1 Coulomb = 106 microCoulomb
1 Coulomb = 109 nanoCoulomb
The problem-solving strategy used in Example A included three steps:
- Identify and list known information in variable form.
- List the unknown (or desired) information in variable form.
- Substitute known values into the Coulomb's law equation and using proper algebraic steps to solve for the unknown information. (In some cases and for some students, it might be easier to first do the algebra using the variables and then perform the substitution as the last step.)
This same problem-solving strategy is demonstrated in Example B below.
|
Example B
Two balloons are charged with an identical quantity and type of charge: -6.25 nC. They are held apart at a separation distance of 61.7 cm. Determine the magnitude of the electrical force of repulsion between them.
|
The problem states the value of Q1 and Q2. Since these values are expressed in units of nanoCoulombs (nC), the conversion to Coulombs must be made. The problem also states the separation distance (d). Since distance is given in units of centimeters (cm), the conversion to meters must also be made. These conversions are required since the units of charge and distance in the Coulomb's constant are Coulombs and meters. The unknown quantity is the electrical force (F). The results of the first two steps are shown in the table below.
|
Given:
Q1 = -6.25 nC = -6.25 x 10-9 C
Q2 = -6.25 nC = -6.25 x 10-9 C
d = 61.7 cm = 0.617 m
|
Find:
Felect = ???
|
The final step of the strategy involves substituting known values into the Coulomb's law equation and using proper algebraic steps to solve for the unknown information. This substitution and algebra is shown below.
Felect = k • Q1 • Q2 / d2
Felect = (9.0 x 109 N•m2/C2) • (6.25 x 10-9 C) • (6.25 x 10-9 C) / (0.617 m)2
Felect = 9.23 x 10-7 N
Note that the "-" sign was dropped from the Q1 and Q2 values prior to substitution into the Coulomb's law equation. As mentioned above, the use of "+" and "-" signs in the equation would result in a positive force value if Q1 and Q2 are like charged and a negative force value if Q1 and Q2 are oppositely charged. The resulting "+" and "-" signs on F signifies whether the force is attractive (a "-" F value) or repulsive (a "+" F value).
|
Example C
Two balloons with charges of +3.37 µC and -8.21 µC attract each other with a force of 0.0626 Newton. Determine the separation distance between the two balloons.
|
The problem states the value of Q1 and Q2. Since these values are in units of microCoulombs (µC), the conversion to Coulombs will be made. The problem also states the electrical force (F). The unknown quantity is the separation distance (d). The results of the first two steps are shown in the table below.
|
Given:
Q1 = +3.37 µC = +3.37 x 10-6 C
Q2 = -8.21 µC = -8.21 x 10-6 C
Felect = -0.0626 N (use a - force value since it is attractive)
|
Find:
d = ???
|
As mentioned above, the use of the "+" and "-" signs is optional. However, if they are used, then they have to be used consistently for the Q values and the F values. Their use in the equation is illustrated in this problem.
The final step of the strategy involves substituting known values into the Coulomb's law equation and using proper algebraic steps to solve for the unknown information. In this case, the algebra is done first and the substitution is performed last. This algebra and substitution is shown below.
Felect = k • Q1 • Q2 / d2
d2 • Felect = k • Q1 • Q2
d2 = k • Q1 • Q2 / Felect
d = SQRT(k • Q1 • Q2) / Felect
d = SQRT [(9.0 x 109 N•m2/C2) • (-8.21 x 10-6 C) • (+3.37 x 10-6 C) / (-0.0626 N)]
d = Sqrt [ +3.98 m2 ]
d = +1.99 m
Comparing Electrical and Gravitational Forces
Electrical force and gravitational force are the two non-contact forces discussed in The Physics Classroom tutorial. Coulomb's law equation for electrical force bears a strong resemblance to Newton's equation for universal gravitation.
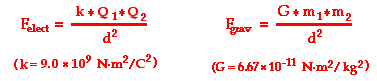
The two equations have a very similar form. Both equations show an inverse square relationship between force and separation distance. And both equations show that the force is proportional to the product of the quantity that causes the force - charge in the case of electrical force and mass in the case of gravitational force. Yet there are some striking differences between these two forces. First, a comparison of the proportionality constants - k versus G - reveals that the Coulomb's law constant (k) is significantly greater than Newton's universal gravitation constant (G). Subsequently a unit of charge will attract a unit of charge with significantly more force than a unit of mass will attract a unit of mass. Second, gravitational forces are only attractive; electrical forces can be either attractive or repulsive.
The inverse square relationship between force and distance that is woven into the equation is common to both non-contact forces. This relationship highlights the importance of separation distance when it comes to the electrical force between charged objects. It is the focus of the next section of Lesson 3.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Coulomb's Law Interactive. You can find it in the Physics Interactives section of our website. The
Coulomb's Law Interactive allows a learner to explore the effect of charge and separation distance upon the amount of electric force between two charged objects.
Check Your Understanding
Use your understanding to answer the following questions. When finished, click the button to view the answers.
1. The Q in Coulomb's law equation stands for the _____.
|
a. mass of a charged object
|
b. # of excess electrons on the object
|
|
c. the current of a charged object
|
d. the distance between charged objects
|
|
e. charge of a charged object
|
|
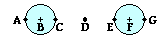
2. The symbol d in Coulomb's law equation represents the distance from ___.
|
a. A to B
|
b. A to D
|
c. B to C
|
d. B to D
|
|
e. C to D
|
f. A to G
|
g. B to F
|
h. C to E
|
3. Determine the electrical force of attraction between two balloons with separate charges of +3.5 x 10-8 C and -2.9 x 10-8 C when separated a distance of 0.65 m.
4. Determine the electrical force of attraction between two balloons that are charged with the opposite type of charge but the same quantity of charge. The charge on the balloons is 6.0 x 10-7 C and they are separated by a distance of 0.50 m.
5. Joann has rubbed a balloon with wool to give it a charge of -1.0 x 10-6 C. She then acquires a plastic golf tube with a charge of +4.0 x 10-6 C localized at a given position. She holds the location of charge on the plastic golf tube a distance of 50.0 cm above the balloon. Determine the electrical force of attraction between the golf tube and the balloon.
6. A balloon with a charge of 4.0 µC is held a distance of 0.70 m from a second balloon having the same charge. Calculate the magnitude of the repulsive force.
7. At what distance of separation must two 1.00-microCoulomb charges be positioned in order for the repulsive force between them to be equivalent to the weight (on Earth) of a 1.00-kg mass?