Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 As discussed in a previous part of Lesson 2, total system momentum is conserved for collisions between objects in an isolated system. The momentum lost by one object is equal to the momentum gained by another object. For collisions occurring in an isolated system, there are no exceptions to this law. This law becomes a powerful tool in physics because it allows for predictions of the before- and after-collision velocities (or mass) of an object. In this portion of Lesson 2, the law of momentum conservation will be used to make such predictions. The law of momentum conservation will be combined with the use of a "momentum table" and some algebra skills to solve problems involving collisions occurring in isolated systems.
As discussed in a previous part of Lesson 2, total system momentum is conserved for collisions between objects in an isolated system. The momentum lost by one object is equal to the momentum gained by another object. For collisions occurring in an isolated system, there are no exceptions to this law. This law becomes a powerful tool in physics because it allows for predictions of the before- and after-collision velocities (or mass) of an object. In this portion of Lesson 2, the law of momentum conservation will be used to make such predictions. The law of momentum conservation will be combined with the use of a "momentum table" and some algebra skills to solve problems involving collisions occurring in isolated systems.
Example 1
Consider the following problem:
A 15-kg medicine ball is thrown at a velocity of 20 km/hr to a 60-kg person who is at rest on ice. The person catches the ball and subsequently slides with the ball across the ice. Determine the velocity of the person and the ball after the collision.
Such a motion can be considered as a collision between a person and a medicine ball. Before the collision, the ball has momentum and the person does not. The collision causes the ball to lose momentum and the person to gain momentum. After the collision, the ball and the person travel with the same velocity (v) across the ice.
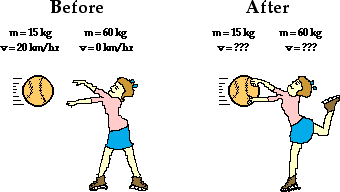
If it can be assumed that the effect of friction between the person and the ice is negligible, then the collision has occurred in an isolated system. Momentum should be conserved and the post-collision velocity (v) can be determined using a momentum table as shown below.
| |
Before Collision
|
After Collision
|
|
Person
|
0
|
(60 kg) • v
|
|
Medicine ball
|
(15 kg) • (20 km/hr)
= 300 kg • km/hr
|
(15 kg) • v
|
|
Total
|
300 kg • km/hr
|
300
|
Observe in the table above that the known information about the mass and velocity of the two objects was used to determine the before-collision momenta of the individual objects and the total momentum of the system. Since momentum is conserved, the total momentum after the collision is equal to the total momentum before the collision. Finally, the expressions 60 kg • v and 15 kg • v were used for the after-collision momentum of the person and the medicine ball. To determine v (the velocity of both the objects after the collision), the sum of the individual momentum of the two objects can be set equal to the total system momentum. The following equation results:
60 • v + 15 • v = 300
75 • v = 300
v = 4 km/hr
Using algebra skills, it can be shown that v = 4 km/hr. Both the person and the medicine ball move across the ice with a velocity of 4 km/hr after the collision. (NOTE: The unit km/hr is the unit on the answer since the original velocity as stated in the question had units of km/hr.)
Example 2
Now consider a similar problem involving momentum conservation.
A 0.150-kg baseball moving at a speed of 45.0 m/s crosses the plate and strikes the 0.250-kg catcher's mitt (originally at rest). The catcher's mitt immediately recoils backwards (at the same speed as the ball) before the catcher applies an external force to stop its momentum. If the catcher's hand is in a relaxed state at the time of the collision, it can be assumed that no net external force exists and the law of momentum conservation applies to the baseball-catcher's mitt collision. Determine the post-collision velocity of the mitt and ball.
Before the collision, the ball has momentum and the catcher's mitt does not. The collision causes the ball to lose momentum and the catcher's mitt to gain momentum. After the collision, the ball and the mitt move with the same velocity (v).
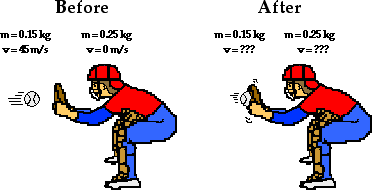
The collision between the ball and the catcher's mitt occurs in an isolated system, total system momentum is conserved. Thus, the total momentum before the collision (possessed solely by the baseball) equals the total momentum after the collision (shared by the baseball and the catcher's mitt). The table below depicts this principle of momentum conservation.
| |
Before Collision
|
After Collision
|
|
Ball
|
0.15 kg • 45 m/s = 6.75 kg•m/s
|
(0.15 kg) • v
|
|
Catcher's Mitt
|
0
|
(0.25 kg) • v
|
|
Total
|
6.75 kg•m/s
|
6.75 kg•m/s
|
Observe in the table above that the known information about the mass and velocity of baseball and the catcher's mitt was used to determine the before-collision momenta of the individual objects and the total momentum of the system. Since momentum is conserved, the total momentum after the collision is equal to the total momentum before the collision. Finally, the expression 0.15 • v and 0.25 • v are used for the after-collision momentum of the baseball and catcher's mitt. To determine v (the velocity of both objects after the collision), the sum of the individual momentum of the two objects is set equal to the total system momentum. The following equation results:
0.15 kg • v + 0.25 kg • v = 6.75 kg•m/s
0.40 kg • v = 6.75 kg•m/s
v = 16.9 m/s
Using algebra skills, it can be shown that v = 16.9 m/s. Both the baseball and the catcher's mitt move with a velocity of 16.9 m/s immediately after the collision and prior to the moment that the catcher begins to apply an external force.
The two collisions above are examples of inelastic collisions. Technically, an inelastic collision is a collision in which the kinetic energy of the system of objects is not conserved. In an inelastic collision, the kinetic energy of the colliding objects is transformed into other non-mechanical forms of energy such as heat energy and sound energy. The subject of energy will be treated in a later unit of The Physics Classroom. To simplify matters, we will consider any collisions in which the two colliding objects stick together and move with the same post-collision speed to be an extreme example of an inelastic collision.
Example 3
Now we will consider the analysis of a collision in which the two objects do not stick together. In this collision, the two objects will bounce off each other. While this is not technically an elastic collision, it is more elastic than the previous collisions in which the two objects stick together.
A 3000-kg truck moving with a velocity of 10 m/s hits a 1000-kg parked car. The impact causes the 1000-kg car to be set in motion at 15 m/s. Assuming that momentum is conserved during the collision, determine the velocity of the truck immediately after the collision.
In this collision, the truck has a considerable amount of momentum before the collision and the car has no momentum (it is at rest). After the collision, the truck slows down (loses momentum) and the car speeds up (gains momentum).

The collision can be analyzed using a momentum table similar to the above situations.
| |
Before Collision
|
After Collision
|
|
Truck
|
3000 • 10 = 30 000
|
3000 • v
|
|
Car
|
0
|
1000 • 15 = 15 000
|
|
Total
|
30 000
|
30 000
|
Observe in the table above that the known information about the mass and velocity of the truck and car was used to determine the before-collision momenta of the individual objects and the total momentum of the system. Since momentum is conserved, the total momentum after the collision is equal to the total momentum before the collision. The after-collision velocity of the car is used (in conjunction with its mass) to determine its momentum after the collision. Finally, the expression 3000•v was used for the after-collision momentum of the truck (v is the velocity of the truck after the collision). To determine v (the velocity of the truck), the sum of the individual after-collision momentum of the two objects is set equal to the total momentum. The following equation results:
3000*v + 15 000 = 30 000
3000*v = 15 000
v = 5.0 m/s
Using algebra skills, it can be shown that v = 5.0 m/s. The truck's velocity immediately after the collision is 5.0 m/s. As predicted, the truck has lost momentum (slowed down) and the car has gained momentum.

 The three problems above illustrate how the law of momentum conservation can be used to solve problems in which the after-collision velocity of an object is predicted based on mass-velocity information. There are additional practice problems (with accompanying solutions) later in this lesson that are worth the practice. However, be certain that you don't come to believe that physics is merely an applied mathematics course that is devoid of concepts. For certain, mathematics is applied in physics. However, physics is about concepts and the variety of means in which they are represented. Mathematical representations are just one of the many representations of physics concepts. Avoid merely treating these collision problems as mere mathematical exercises. Take the time to understand the concept of momentum conservation that provides the basis of their solution.
The three problems above illustrate how the law of momentum conservation can be used to solve problems in which the after-collision velocity of an object is predicted based on mass-velocity information. There are additional practice problems (with accompanying solutions) later in this lesson that are worth the practice. However, be certain that you don't come to believe that physics is merely an applied mathematics course that is devoid of concepts. For certain, mathematics is applied in physics. However, physics is about concepts and the variety of means in which they are represented. Mathematical representations are just one of the many representations of physics concepts. Avoid merely treating these collision problems as mere mathematical exercises. Take the time to understand the concept of momentum conservation that provides the basis of their solution.
The next section of this lesson involves examples of problems that provide a real test of your conceptual understanding of momentum conservation in collisions. Before proceeding with the practice problems, be sure to try a few of the more conceptual questions that follow.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Exploding Carts Interactive and/or our
Collision Carts Ineractive. These Interactives can be found in the Physics Interactive section of our website and provide an interactive experience in analyzing the momentum of individual objects and systems of objects in collisions.