Coulomb’s Law of Force - Complete Toolkit
Objectives
- To understand that objects are charged if there is an imbalance of protons and electrons and to calculate the amount of charge on an object if given the number of excess protons or electrons.
- To use Coulomb’s Law equation to make predictions of the effect of alteration in the quantity of charge or the separation distance upon the amount of electrostatic force.
- To use Coulomb’s Law equation to algebraically solve for an unknown quantity (F, d, Θ1 or Θ2) in a physics word problem.
- To combine Coulomb’s Law equation with Newton’s second law, free-body diagrams and trigonometric functions to analyze physical situations that include interacting charges.
Readings from The Physics Classroom Tutorial
- The Physics Classroom Tutorial, Static Electricity Chapter, Lesson 3
Interactive Simulations
- Coulomb’s Law Interactive
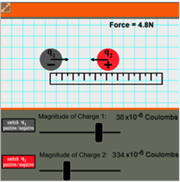
Many students can do the math involved with Coulomb’s equation, but may have little comprehension of its significance. This simulation lets students visualize charge interaction to see why Coulomb’s Law works mathematically. Switch the sign of the charge, change quantity of charge, and move the charges around on a grid. Students will see a mathematical pattern emerge that relates force to separation distance and magnitude of charge.
- PhET: Charges and Fields

In this model, learners move charges around a simulated electric field to determine how certain variables affect interactions among charged bodies. First, drag a positive or negative charge (or both) onto the field, then place small positive test charges. Drag a sensor to display the voltage at any point on the field or plot equipotential lines. A virtual tape measure is also provided to calculate distance. Force vectors are automatically generated. Register with PhET (it’s free) to access a set of teacher-contributed lessons, Student Guides, and Power Point presentations developed specifically to go with this simulation.
- Point Charge Forces in 1D Model
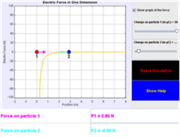
This very simple Java model investigates the electric force that one particle exerts on another. It promotes understanding of Coulomb’s Law in three ways: 1) Vector arrows provide a visual way to connect the magnitude of force with changing position; 2) Particle 2 can be dragged left or right to sample the force at various locations; and 3) A graph can be displayed that shows electric force as a function of time. Force values are generated in a table.
Video and Animations
- UCLA Physics Videos

"But why does Coulomb's Law work?" asks the student. This video-demo is a powerful way to illustrate the math. UCLA video host James Lincoln uses a Coulomb apparatus with a "twist": a neon laser that measures the small amount of twist on the wire in the apparatus. Reflected light from the laser is displayed on a chart. Using the visual display, can students figure out what distance to move the spheres apart to produce half the force? If they use Coulomb's Law, they can!
- PSSC Film Collection: Coulomb’s Law

In the 1950’s, the National Science Foundation supported the Physical Science Study Committee in developing a set of instructional videos for high school physics. Their value lies in more than history. They provide highly visual ways to see physics in action through use of low-tech materials. In this video, noted Princeton physicist Eric Rogers demonstrates charge interaction in ways we bet you’ve never seen. The steel ball-spring balance system is a great way to illustrate Coulomb’ Law in action. Don’t miss the last 5 minutes: Rogers places a young girl in a metal cage, which he then charges with electricity. He demonstrates through the inverse square law that his trusting assistant is not harmed by the charge.
- MIT: Electrostatics Visualizations

Caveat: We recommend this resource with the following precaution -- This is one of the best collections on the web for helping students visualize the invisible processes involved in charge interaction. However, the file formats will not play in all browsers, especially Edge or Chrome. It’s still worth your time to browse the collection to see what you can open in Firefox or with an older version of Java. We understand MIT is working to update the resources to HTML and will let you know when this happens.
- Physlet Physics: Charge and Coulomb’s Law
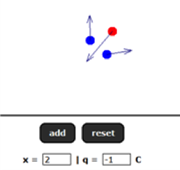
This animation lets students explore charge by placing charged particles in a virtual electric field. It gives guided instruction for investigating charges of equal or unequal magnitude and charges with the same or different polarities. Editor’s Note: be sure your students read the accompanying text explanation! The authors do a great job of explaining why the model has limitations – because nature doesn’t allow us to create particles without paying attention to conservation of charge.
Labs and Investigations
- The Physics Classroom, The Laboratory, Coulomb’s Law Lab
Students make measurements (mass, separation distance, string length) in order to determine the number of electrons transferred to two balloons when rubbed against animal fur. Charged balloons are hung by light strings from a common support.
Link: http://www.physicsclassroom.com/lab#estatic
Digital Labs
- Electric Field: What is Wrong? Package
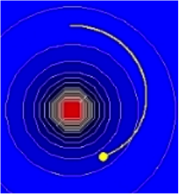
This resource employs the pedagogical method known as “Intentionally Incorrect Simulation”. It consists of a collection of models for electrostatics with errors intentionally built into each model. Students can move charges around and see the force, observe the electric field generated by charge configurations, and observe the motion of test particles in electric fields. Can you identify the errors? Editor’s Note: You can run the sims as JRE (Java Run Environment) or download them as JAR files to customize or modify the source code.
- Ranking Tasks: Three Charged Particles
This model displays up to three charged objects, one at each corner of an equilateral triangle. The charges have different magnitudes – your job is to rank the charges from largest-to-smallest magnitude. You can drag the charges around to see the effect on the net force on each charge.
Demonstration Ideas
- UCLA Physics Labs: Electrostatics and Coulomb’s Law

This web page offers a discussion of fundamental electrostatics theory, pith ball and electrophorus demonstration ideas, and a classroom experiment using a traditional electroscope to investigate how electrostatic interaction is affected by humidity. Editor’s Note: Electroscopes with capacitor plates and charge samplers are readily available from science supply stores for ~ $200.00. You can set up some great labs without the $1400 expense of a complete Coulomb Apparatus.
Minds On Physics Internet Modules:
The Minds On Physics Internet Modules are a collection of interactive questioning modules that target a student’s conceptual understanding. Each question is accompanied by detailed help that addresses the various components of the question.
- Static Electricity, Ass’t SE8 - Coulomb’s Law Equation as a Guide to Thinking
- Static Electricity, Ass’t SE9 - Coulomb’s Law Calculations
Concept Building Exercises:
- The Curriculum Corner, Static Electricity, Coulomb’s Law
Problem-Solving Exercises:
- The Calculator Pad, Static Electricity, Problems #1 - #14
Link: http://www.physicsclassroom.com/calcpad/estatics
Science Reasoning Activities:
- Science Reasoning Center, Electrostatics, Charge Interactions
- Science Reasoning Center, Electrostatics, Sticky Tape Experiments
Link: http://www.physicsclassroom.com/reasoning/electrostatics
Historical Connections:
- Charles-Augustin de Coulomb

This short biography from Magnet Academy at Florida State University takes a look at the contributions of Charles Augustin de Coulomb, the 18th Century French scientist whose experiments with a torsion balance gave rise to one of the fundamental principles of electromagnetism. Coulomb’s Law defines the mathematical relationship between electrically-charged particles and was a cornerstone in the development of electromagnetic theory.
- Magnet Academy: The Torsion Balance

This tutorial from the National High Magnetic Field Laboratory explores the historic instrument known as a torsion balance. By carefully recording the measurements obtained with a torsion balance, Coulomb was able to establish the law that bears his name.
Common Misconception:
- A Coulomb of Charge
Students mistakenly believe that a Coulomb of charge is a small amount of charge. After all, “there is just 1 coulomb … not 20 or 200 or 2 million.” Convince students that a Coulomb of charge is a very large amount of charge by calculating the force of interaction between two balloons with a Coulomb of charge located at your school and some distance away at the next nearest high school. The calculation quickly convinces students that a Coulomb of charge is a very large amount of charge. An object with 1 C of charge has gained or lost 6.25x1018 electrons. For comparison sake, briskly rubbing a balloon on your head 10 times may contribute 2-trillion (2x1012) electrons to the balloon. This figure is far short of the 6.25x 1018 electrons required for a Coulomb of charge. The fact that a Coulomb of charge is a large amount of charge explains why many Coulomb’s law problems express the quantity of charge in units of microCoulombs (µC) and nanoCoulombs (nC).
- Separation Distance
The Coulomb’s Law equation presumes that charged objects act as point charges, with all their charge concentrated at a point. As such, the separation distance d in the Coulomb’s law equation is the distance between these two points. Since objects generally do not occupy points in space, it is important that the measurement of separation distance be made from the centers of the two interacting objects (or at least from the centers of their charge). Students often self-define separation distance to be the distance between the nearest edges of the two interacting objects.
Elsewhere on the Web:
- MIT Open Courseware: Coulomb’s Law Lecture Notes

This is a freely-accessible chapter from MIT’s TEAL Project (Technology Enabled Active Learning) related to Coulomb’s Law. The 45-page document takes a deep dive into the Coulomb interaction for two point charges, as well as multiple charges. It’s a great resource for teachers wanting to brush up or broaden their understanding of electric dipole, forces on charged particles, and problem-solving with 3-and 4-point-charge systems.
- CASES Online: A Tale of Two Charges

This activity developed for Emory University’s Cases Online presents a unique task: Write a 21st-Century encyclopedia article about Coulomb’s Law. The article must be scientifically accurate and provide links to digital media that illustrate the concept (to include animations, simulations, and tutorials). Teacher-generated ideas are kept to a minimum, challenging students to locate, analyze, and evaluate resources themselves. Editor’s Note: Access to CASES Online is free, but requires user registration to open lesson plans and Student Guides.
Standards:
A. Next Generation Science Standards (NGSS)
Performance Expectations
- HS-PS2-4: Use mathematical representations of Coulomb’s Law to describe and predict the gravitational and electrostatic forces between objects.
Disciplinary Core Ideas - Types of Interactions
- HS-PS2.B.1: Coulomb’s Law provides the mathematical model to describe and predict the effects of electrostatic forces between distant objects.
- HS-PS2.B.2: Forces at a distance are explained by fields (gravitational, electric, and magnetic) permeating space that can transfer energy through space.
Crosscutting Concepts
Patterns
- Different patterns may be observed at each of the scales at which a system is studied and can provide evidence for causality in explanation of phenomena.
Scale, Proportion, and Quantity
- The significance of a phenomenon is dependent on the scale, proportion, and quantity at which it occurs.
- Time, space, and energy phenomena can be observed at various scales using models to study systems that are too large or too small.
Structure and Function
- Complex and microscopic structures and systems can be visualized, modeled, and used to describe how their function depends on the shapes, composition, and relationships among its parts, therefore complex natural structures/systems can be analyzed to determine how they function.
Science and Engineering Practices
Practice #3: Constructing Explanations
- Construct an explanation that includes qualitative or quantitative relationships between variables that predict phenomena.
- Construct and review an explanation based on valid and reliable evidence obtained from a variety of sources (including students’ own investigations, models, simulations, and peer review) and the assumption that theories and laws that describe the natural world operate today as they did in the past and will continue to do so in the future.
Practice #4: Developing and Using Models
- Develop and/or use a model to generate data to support explanations, analyze systems, or solve problems.
- Use a model to provide mechanistic accounts of phenomena.
Practice #6: Obtaining, Evaluating, and Communicating Information
- Evaluate the validity and reliability of multiple claims that appear in scientific and technical texts or media reports, verifying the data when possible.
- Critically read scientific literature adapted for classroom use to determine central ideas and obtain scientific/technical information.
Practice #8: Using Mathematics and Computational Thinking
- Use mathematical representations of phenomena to describe explanations.
- Create or revise a simulation of a phenomenon, designed device, process, or system.