 There are certain formulas in Physics that are so powerful and so pervasive that they reach the state of popular knowledge. A student of Physics has written such formulas down so many times that they have memorized it without trying to. Certainly to the professionals in the field, such formulas are so central that they become engraved in their minds. In the field of Modern Physics, there is E = m • c2. In the field of Newtonian Mechanics, there is Fnet = m • a. In the field of Wave Mechanics, there is v = f • λ. And in the field of current electricity, there is ΔV = I • R.
There are certain formulas in Physics that are so powerful and so pervasive that they reach the state of popular knowledge. A student of Physics has written such formulas down so many times that they have memorized it without trying to. Certainly to the professionals in the field, such formulas are so central that they become engraved in their minds. In the field of Modern Physics, there is E = m • c2. In the field of Newtonian Mechanics, there is Fnet = m • a. In the field of Wave Mechanics, there is v = f • λ. And in the field of current electricity, there is ΔV = I • R.
The predominant equation which pervades the study of electric circuits is the equation
ΔV = I • R
In words, the electric potential difference between two points on a circuit (ΔV) is equivalent to the product of the current between those two points (I) and the total resistance of all electrical devices present between those two points (R). Through the rest of this unit of The Physics Classroom, this equation will become the most common equation which we see. Often referred to as the Ohm's law equation, this equation is a powerful predictor of the relationship between potential difference, current and resistance.
Ohm's Law as a Predictor of Current
The Ohm's law equation can be rearranged and expressed as
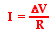
As an equation, this serves as an algebraic recipe for calculating the current if the electric potential difference and the resistance are known. Yet while this equation serves as a powerful recipe for problem solving, it is much more than that. This equation indicates the two variables that would affect the amount of current in a circuit. The current in a circuit is directly proportional to the electric potential difference impressed across its ends and inversely proportional to the total resistance offered by the external circuit. The greater the battery voltage (i.e., electric potential difference), the greater the current. And the greater the resistance, the less the current. Charge flows at the greatest rates when the battery voltage is increased and the resistance is decreased. In fact, a twofold increase in the battery voltage would lead to a twofold increase in the current (if all other factors are kept equal). And an increase in the resistance of the load by a factor of two would cause the current to decrease by a factor of two to one-half its original value.
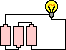
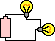
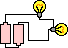
The table below illustrates this relationship both qualitatively and quantitatively for several circuits with varying battery voltages and resistances.
| |
Circuit
Diagram
|
Battery
Voltage
(ΔV)
|
Total
Resistance
( ) )
|
Current
(Amps)
|
|
1.
|

|
1.5 V
|
3 
|
0.50 Amp
|
|
2.
|

|
3.0 V
|
3 Ω
|
1 Amp
|
|
3.
|
|
4.5 V
|
3 
|
1.5 Amp
|
|
4.
|
|
1.5 V
|
6 
|
0.25 Amp
|
|
5.
|
|
3.0 V
|
6 
|
0.5 Amp
|
|
6.
|

|
4.5 V
|
6 Ω
|
0.75 Amp
|
|
7.
|
|
4.5 V
|
9 Ω
|
0.50 Amp
|
Rows 1, 2 and 3 illustrate that the doubling and the tripling of the battery voltage leads to a doubling and a tripling of the current in the circuit. Comparing rows 1 and 4 or rows 2 and 5 illustrates that the doubling of the total resistance serves to halve the current in the circuit.
Because the current in a circuit is affected by the resistance, resistors are often used in the circuits of electrical appliances to affect the amount of current that is present in its various components. By increasing or decreasing the amount of resistance in a particular branch of the circuit, a manufacturer can increase or decrease the amount of current in that branch. Kitchen appliances such as electric mixers and light dimmer switches operate by altering the current at the load by increasing or decreasing the resistance of the circuit. Pushing the various buttons on an electric mixer can change the mode from mixing to beating by reducing the resistance and allowing more current to be present in the mixer. Similarly, turning a dial on a dimmer switch can increase the resistance of its built-in resistor and thus reduce the current.
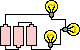
 The diagram below depicts a couple of circuits containing a voltage source (battery pack), a resistor (light bulb) and an ammeter (for measuring current). In which circuit does the light bulb have the greatest resistance? Click the See Answer button to see if you are correct.
The diagram below depicts a couple of circuits containing a voltage source (battery pack), a resistor (light bulb) and an ammeter (for measuring current). In which circuit does the light bulb have the greatest resistance? Click the See Answer button to see if you are correct.
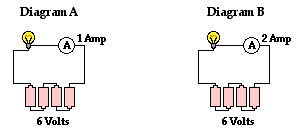
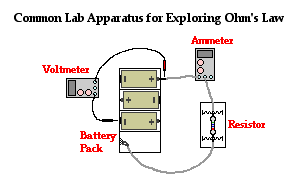 The Ohm's law equation is often explored in physics labs using a resistor, a battery pack, an ammeter, and a voltmeter. An ammeter is a device used to measure the current at a given location. A voltmeter is a device equipped with probes that can be touched to two locations on a circuit to determine the electric potential difference across those locations. By altering the number of cells in the battery pack, the electric potential difference across the external circuit can be varied. The voltmeter can be used to determine this potential difference and the ammeter can be used to determine the current associated with this ΔV. A battery can be added to the battery pack and the process can be repeated several times to yield a set of I-ΔV data. A plot of I versus ΔV will yield a line with a slope that is equivalent to the reciprocal of the resistance of the resistor. This can be compared to the manufacturers stated value to determine the accuracy of the lab data and the validity of the Ohm's law equation.
The Ohm's law equation is often explored in physics labs using a resistor, a battery pack, an ammeter, and a voltmeter. An ammeter is a device used to measure the current at a given location. A voltmeter is a device equipped with probes that can be touched to two locations on a circuit to determine the electric potential difference across those locations. By altering the number of cells in the battery pack, the electric potential difference across the external circuit can be varied. The voltmeter can be used to determine this potential difference and the ammeter can be used to determine the current associated with this ΔV. A battery can be added to the battery pack and the process can be repeated several times to yield a set of I-ΔV data. A plot of I versus ΔV will yield a line with a slope that is equivalent to the reciprocal of the resistance of the resistor. This can be compared to the manufacturers stated value to determine the accuracy of the lab data and the validity of the Ohm's law equation.
Quantities, Symbols, Equations and Units!
The tendency to give attention to units is an essential trait of any good physics student. Many of the difficulties associated with solving problems may be traced back to the failure to give attention to units. As more and more electrical quantities and their respective metric units are introduced in this unit of The Physics Classroom tutorial, it will become increasingly important to organize the information in your head. The table below lists several of the quantities that have been introduced thus far. The symbol, the equation and the associated metric units are also listed for each quantity. It would be wise to refer to this list often or even to make your own copy and add to it as the unit progresses. Some students find it useful to make a fifth column in which the definition of each quantity is stated.
|
Quantity
|
Symbol
|
Equation(s)
|
Standard Metric Unit
|
Other Units
|
|
Potential Difference
(a.k.a. voltage)
|
ΔV
|
ΔV = ΔPE / Q
ΔV = I • R
|
Volt (V)
|
J / C
|
|
Current
|
I
|
I = Q / t
I = ΔV / R
|
Amperes (A)
|
Amp or C / s
or V / Ω
|
|
Power
|
P
|
P = ΔPE / t
(more to come)
|
Watt (W)
|
J / s
|
|
Resistance
|
R
|
R = ρ • L / A
R = ΔV / I
|
Ohm (Ω)
|
V / A
|
|
Energy
|
E or ΔPE
|
ΔPE = ΔV • Q
ΔPE = P • t
|
Joule (J)
|
V • C or
W • s
|
(Note the unit symbol C represents the unit Coulombs.)
The next section of Lesson 3 will involve taking another look at the quantity power. A new equation for power will be introduced by combining two (or more) of the equations in the above table.
We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
DC Circuit Builder Interactive. You can find it in the Physics Interactives section of our website. The
DC Circuit Builder provides the learner with a virtual circuit building kit. Easily drag a voltage source, resistors and wires onto the workspace. Connect them and you have a circuit. Add an ammeter to measure current and use the voltage probes to determine voltage drop. It's that simple. And there's no need to worry about an electric shock (unless of course, you're reading this in the bathtub).
Check Your Understanding
1. Which of the following will cause the current through an electrical circuit to decrease? Choose all that apply.
a. decrease the voltage
b. decrease the resistance
c. increase the voltage
d. increase the resistance
2. A certain electrical circuit contains a battery with three cells, wires and a light bulb. Which of the following would cause the bulb to shine less brightly? Choose all that apply.
a. increase the voltage of the battery (add another cell)
b. decrease the voltage of the battery (remove a cell)
c. decrease the resistance of the circuit
d. increase the resistance of the circuit
3. You have likely been warned to avoid contact with electrical appliances or even electrical outlets when your hands are wet. Such contact is more dangerous when your hands are wet (vs. dry) because wet hands cause ____.
a. the voltage of the circuit to be higher
b. the voltage of the circuit to be lower
c. your resistance to be higher
d. your resistance to be lower
e. the current through you to be lower
4. If the resistance of a circuit were tripled, then the current through the circuit would be ____.
a. one-third as much
b. three times as much
c. unchanged
d. ... nonsense! There would be no way to make such a prediction.
5. If the voltage across a circuit is quadrupled, then the current through the circuit would be ____.
a. one-fourth as much
b. four times as much
c. unchanged
d. ... nonsense! There would be no way to make such a prediction.
6. A circuit is wired with a power supply, a resistor and an ammeter (for measuring current). The ammeter reads a current of 24 mA (milliAmps). Determine the new current if the voltage of the power supply was ...
a. ... increased by a factor of 2 and the resistance was held constant.
b. ... increased by a factor of 3 and the resistance was held constant.
c. ... decreased by a factor of 2 and the resistance was held constant.
d. ... held constant and the resistance was increased by a factor of 2.
e. ... held constant and the resistance was increased by a factor of 4.
f. ... held constant and the resistance was decreased by a factor of 2.
g. ... increased by a factor of 2 and the resistance was increased by a factor of 2.
h. ... increased by a factor of 3 and the resistance was decreased by a factor of 2.
i. ... decreased by a factor of 2 and the resistance was increased by a factor of 2.
7. Use the Ohm's law equation to provide numerical answers to the following questions:
a. An electrical device with a resistance of 3.0 Ω will allow a current of 4.0 amps to flow through it if a voltage drop of ________ Volts is impressed across the device.
b. When a voltage of 120 V is impressed across an electric heater, a current of 10.0 amps will flow through the heater if the resistance is ________ Ω.
c. A flashlight that is powered by 3 Volts and uses a bulb with a resistance of 60 Ω will have a current of ________ Amps.
8. Use the Ohm's law equation to determine the missing values in the following circuits.
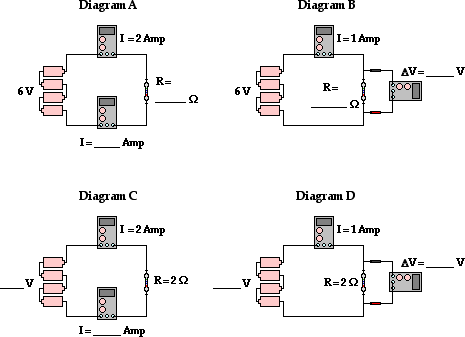
9. Refer to question 8 above. In the circuits of diagrams A and B, what method was used to control the current in the circuits? And in the circuits of diagrams C and D, what method was used to control the current in the circuits?