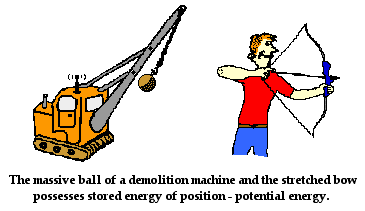
 An object can store energy as the result of its position. For example, the heavy ball of a demolition machine is storing energy when it is held at an elevated position. This stored energy of position is referred to as potential energy. Similarly, a drawn bow is able to store energy as the result of its position. When assuming its usual position (i.e., when not drawn), there is no energy stored in the bow. Yet when its position is altered from its usual equilibrium position, the bow is able to store energy by virtue of its position. This stored energy of position is referred to as potential energy. Potential energy is the stored energy of position possessed by an object.
An object can store energy as the result of its position. For example, the heavy ball of a demolition machine is storing energy when it is held at an elevated position. This stored energy of position is referred to as potential energy. Similarly, a drawn bow is able to store energy as the result of its position. When assuming its usual position (i.e., when not drawn), there is no energy stored in the bow. Yet when its position is altered from its usual equilibrium position, the bow is able to store energy by virtue of its position. This stored energy of position is referred to as potential energy. Potential energy is the stored energy of position possessed by an object.
Gravitational Potential Energy
The two examples above illustrate the two forms of potential energy to be discussed in this course - gravitational potential energy and elastic potential energy.  Gravitational potential energy is the energy stored in an object as the result of its vertical position or height. The energy is stored as the result of the gravitational attraction of the Earth for the object. The gravitational potential energy of the massive ball of a demolition machine is dependent on two variables - the mass of the ball and the height to which it is raised. There is a direct relation between gravitational potential energy and the mass of an object. More massive objects have greater gravitational potential energy. There is also a direct relation between gravitational potential energy and the height of an object. The higher that an object is elevated, the greater the gravitational potential energy. These relationships are expressed by the following equation:
Gravitational potential energy is the energy stored in an object as the result of its vertical position or height. The energy is stored as the result of the gravitational attraction of the Earth for the object. The gravitational potential energy of the massive ball of a demolition machine is dependent on two variables - the mass of the ball and the height to which it is raised. There is a direct relation between gravitational potential energy and the mass of an object. More massive objects have greater gravitational potential energy. There is also a direct relation between gravitational potential energy and the height of an object. The higher that an object is elevated, the greater the gravitational potential energy. These relationships are expressed by the following equation:
PEgrav = mass • g • height
PEgrav = m *• g • h
In the above equation, m represents the mass of the object, h represents the height of the object and g represents the gravitational field strength (9.8 N/kg on Earth) - sometimes referred to as the acceleration of gravity.
To determine the gravitational potential energy of an object, a zero height position must 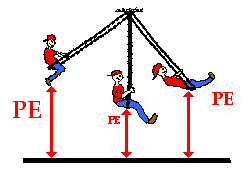 first be arbitrarily assigned. Typically, the ground is considered to be a position of zero height. But this is merely an arbitrarily assigned position that most people agree upon. Since many of our labs are done on tabletops, it is often customary to assign the tabletop to be the zero height position. Again this is merely arbitrary. If the tabletop is the zero position, then the potential energy of an object is based upon its height relative to the tabletop. For example, a pendulum bob swinging to and from above the tabletop has a potential energy that can be measured based on its height above the tabletop. By measuring the mass of the bob and the height of the bob above the tabletop, the potential energy of the bob can be determined.
first be arbitrarily assigned. Typically, the ground is considered to be a position of zero height. But this is merely an arbitrarily assigned position that most people agree upon. Since many of our labs are done on tabletops, it is often customary to assign the tabletop to be the zero height position. Again this is merely arbitrary. If the tabletop is the zero position, then the potential energy of an object is based upon its height relative to the tabletop. For example, a pendulum bob swinging to and from above the tabletop has a potential energy that can be measured based on its height above the tabletop. By measuring the mass of the bob and the height of the bob above the tabletop, the potential energy of the bob can be determined.
Since the gravitational potential energy of an object is directly proportional to its height above the zero position, a doubling of the height will result in a doubling of the gravitational potential energy. A tripling of the height will result in a tripling of the gravitational potential energy.
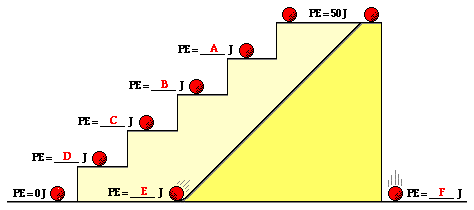
 Use this principle to determine the blanks in the following diagram. Knowing that the potential energy at the top of the tall platform is 50 J, what is the potential energy at the other positions shown on the stair steps and the incline?
Use this principle to determine the blanks in the following diagram. Knowing that the potential energy at the top of the tall platform is 50 J, what is the potential energy at the other positions shown on the stair steps and the incline?
Elastic Potential Energy
 The second form of potential energy that we will discuss is elastic potential energy. Elastic potential energy is the energy stored in elastic materials as the result of their stretching or compressing. Elastic potential energy can be stored in rubber bands, bungee chords, trampolines, springs, an arrow drawn into a bow, etc. The amount of elastic potential energy stored in such a device is related to the amount of stretch of the device - the more stretch, the more stored energy.
The second form of potential energy that we will discuss is elastic potential energy. Elastic potential energy is the energy stored in elastic materials as the result of their stretching or compressing. Elastic potential energy can be stored in rubber bands, bungee chords, trampolines, springs, an arrow drawn into a bow, etc. The amount of elastic potential energy stored in such a device is related to the amount of stretch of the device - the more stretch, the more stored energy.
Springs are a special instance of a device that can store elastic potential energy due to either compression or stretching. A force is required to compress a spring; the more compression there is, the more force that is required to compress it further. For certain springs, the amount of force is directly proportional to the amount of stretch or compression (x); the constant of proportionality is known as the spring constant (k).
Fspring = k • x
Such springs are said to follow Hooke's Law. If a spring is not stretched or compressed, then there is no elastic potential energy stored in it. The spring is said to be at its equilibrium position. The equilibrium position is the position that the spring naturally assumes when there is no force applied to it. In terms of potential energy, the equilibrium position could be called the zero-potential energy position. There is a special equation for springs that relates the amount of elastic potential energy to the amount of stretch (or compression) and the spring constant. The equation is
PEspring = 0.5 • k • x2
where k = spring constant
x = amount of compression
(relative to equilibrium position)
To summarize, potential energy is the energy that is stored in an object due to its position relative to some zero position. An object possesses gravitational potential energy if it is positioned at a height above (or below) the zero height. An object possesses elastic potential energy if it is at a position on an elastic medium other than the equilibrium position.
Check Your Understanding
Check your understanding of the concept of potential energy by answering the following questions. When finished, click the button to view the answers.
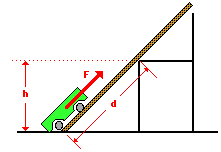 1. A cart is loaded with a brick and pulled at constant speed along an inclined plane to the height of a seat-top. If the mass of the loaded cart is 3.0 kg and the height of the seat top is 0.45 meters, then what is the potential energy of the loaded cart at the height of the seat-top?
1. A cart is loaded with a brick and pulled at constant speed along an inclined plane to the height of a seat-top. If the mass of the loaded cart is 3.0 kg and the height of the seat top is 0.45 meters, then what is the potential energy of the loaded cart at the height of the seat-top?
2. If a force of 14.7 N is used to drag the loaded cart (from previous question) along the incline for a distance of 0.90 meters, then how much work is done on the loaded cart?
Note that the work done to lift the loaded cart up the inclined plane at constant speed is equal to the potential energy change of the cart. This is not coincidental! The reason for the relation between the potential energy change of the cart and the work done upon it is the subject of Lesson 2.