Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 In a previous part of Lesson 1, it was said that
In a previous part of Lesson 1, it was said that
In a collision, an object experiences a force for a given amount of time that results in its mass undergoing a change in velocity (i.e., that results in a momentum change).
There are four physical quantities mentioned in the above statement - force, time, mass, and velocity change. The force multiplied by the time is known as the impulse and the mass multiplied by the velocity change is known as the change in momentum. The impulse experienced by an object is always equal to the change in its momentum. In terms of equations, this was expressed as
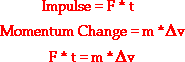
This is known as the impulse-momentum change theorem.
 In this part of Lesson 1, we will examine some real-world applications of the impulse-momentum change theorem. We will examine some physics in action in the real world. In particular, we will focus upon
In this part of Lesson 1, we will examine some real-world applications of the impulse-momentum change theorem. We will examine some physics in action in the real world. In particular, we will focus upon
As an effort is made to apply the impulse-momentum change theorem to a variety of real-world situations, keep in mind that the goal is to use the equation as a guide to thinking about how an alteration in the value of one variable might affect the value of another variable.
The Effect of Collision Time Upon the Force
First we will examine the importance of the collision time in affecting the amount of force that an object experiences during a collision. In a previous part of Lesson 1, it was mentioned that force and time are inversely proportional. An object with 100 units of momentum must experience 100 units of impulse in order to be brought to a stop. Any combination of force and time could be used to produce the 100 units of impulse necessary to stop an object with 100 units of momentum. This is depicted in the table below.
Combinations of Force and Time Required to Produce 100 units of Impulse
|
Force
|
Time
|
Impulse
|
|
100
|
1
|
100
|
|
50
|
2
|
100
|
|
25
|
4
|
100
|
|
10
|
10
|
100
|
|
4
|
25
|
100
|
|
2
|
50
|
100
|
|
1
|
100
|
100
|
|
0.1
|
1000
|
100
|
Observe that the greater the time over which the collision occurs, the smaller the force acting upon the object. Thus, to minimize the effect of the force on an object involved in a collision, the time must be increased. And to maximize the effect of the force on an object involved in a collision, the time must be decreased.
Big t ... Little F: Some Applications
There are several real-world applications of these phenomena. One example is the use of air bags in automobiles. Air bags are used in automobiles because they are able to minimize the effect of the force on an object involved in a collision. Air bags accomplish this by extending the time  required to stop the momentum of the driver and passenger. When encountering a car collision, the driver and passenger tend to keep moving in accord with Newton's first law. Their motion carries them towards a windshield that results in a large force exerted over a short time in order to stop their momentum. If instead of hitting the windshield, the driver and passenger hit an air bag, then the time duration of the impact is increased. When hitting an object with some give such as an air bag, the time duration might be increased by a factor of 100. Increasing the time by a factor of 100 will result in a decrease in force by a factor of 100. Now that's physics in action.
required to stop the momentum of the driver and passenger. When encountering a car collision, the driver and passenger tend to keep moving in accord with Newton's first law. Their motion carries them towards a windshield that results in a large force exerted over a short time in order to stop their momentum. If instead of hitting the windshield, the driver and passenger hit an air bag, then the time duration of the impact is increased. When hitting an object with some give such as an air bag, the time duration might be increased by a factor of 100. Increasing the time by a factor of 100 will result in a decrease in force by a factor of 100. Now that's physics in action.
The same principle explains why dashboards are padded. If the air bags do not deploy (or are not installed in a car), then the driver and passengers run the risk of stopping their momentum by means of a collision with the windshield or the dashboard. If the driver or passenger should hit the dashboard, then the force and time required to stop their momentum is exerted by the dashboard. Padded dashboards provide some give in such a collision and serve to extend the time duration of the impact, thus minimizing the effect of the force. This same principle of padding a potential impact area can be observed in gymnasiums (underneath the basketball hoops), in pole-vaulting pits, in baseball gloves and goalie mitts, on the fist of a boxer, inside the helmet of a football player, and on gymnastic mats. Now that's physics in action.
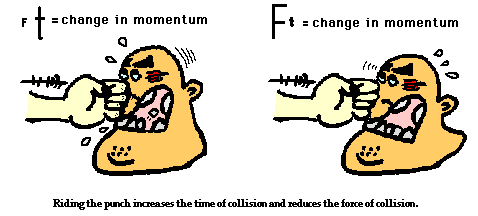
Fans of boxing frequently observe this same principle of minimizing the effect of a force by extending the time of collision. When a boxer recognizes that he will be hit in the head by his opponent, the boxer often relaxes his neck and allows his head to move backwards upon impact. In the boxing world, this is known as riding the punch. A boxer rides the punch in order to extend the time of impact of the glove with their head. Extending the time results in decreasing the force and thus minimizing the effect of the force in the collision. Merely increasing the collision time by a factor of ten would result in a tenfold decrease in the force. Now that's physics in action.
 Nylon ropes are used in the sport of rock-climbing for the same reason. Rock climbers attach themselves to the steep cliffs by means of nylon ropes. If a rock climber should lose her grip on the rock, she will begin to fall. In such a situation, her momentum will ultimately be halted by means of the rope, thus preventing a disastrous fall to the ground below. The ropes are made of nylon or similar material because of its ability to stretch. If the rope is capable of stretching upon being pulled taut by the falling climber's mass, then it will apply a force upon the climber over a longer time period. Extending the time over which the climber's momentum is broken results in reducing the force exerted on the falling climber. For certain, the rock climber can appreciate minimizing the effect of the force through the use of a longer time of impact. Now that's physics in action.
Nylon ropes are used in the sport of rock-climbing for the same reason. Rock climbers attach themselves to the steep cliffs by means of nylon ropes. If a rock climber should lose her grip on the rock, she will begin to fall. In such a situation, her momentum will ultimately be halted by means of the rope, thus preventing a disastrous fall to the ground below. The ropes are made of nylon or similar material because of its ability to stretch. If the rope is capable of stretching upon being pulled taut by the falling climber's mass, then it will apply a force upon the climber over a longer time period. Extending the time over which the climber's momentum is broken results in reducing the force exerted on the falling climber. For certain, the rock climber can appreciate minimizing the effect of the force through the use of a longer time of impact. Now that's physics in action.
 In racket and bat sports, hitters are often encouraged to follow-through when striking a ball. High-speed films of the collisions between bats/rackets and balls have shown that the act of following through serves to increase the time over which a collision occurs. This increase in time must result in a change in some other variable in the impulse-momentum change theorem. Surprisingly, the variable that is dependent upon the time in such a situation is not the force. The force in hitting is dependent upon how hard the hitter swings the bat or racket, not the time of impact. Instead, the follow-through increases the time of collision and subsequently contributes to an increase in the velocity change of the ball. By following through, a hitter can hit the ball in such a way that it leaves the bat or racket with more velocity (i.e., the ball is moving faster). In tennis, baseball, racket ball, etc., giving the ball a high velocity often leads to greater success. Now that's physics in action.
In racket and bat sports, hitters are often encouraged to follow-through when striking a ball. High-speed films of the collisions between bats/rackets and balls have shown that the act of following through serves to increase the time over which a collision occurs. This increase in time must result in a change in some other variable in the impulse-momentum change theorem. Surprisingly, the variable that is dependent upon the time in such a situation is not the force. The force in hitting is dependent upon how hard the hitter swings the bat or racket, not the time of impact. Instead, the follow-through increases the time of collision and subsequently contributes to an increase in the velocity change of the ball. By following through, a hitter can hit the ball in such a way that it leaves the bat or racket with more velocity (i.e., the ball is moving faster). In tennis, baseball, racket ball, etc., giving the ball a high velocity often leads to greater success. Now that's physics in action.
You undoubtedly recall other illustrations of this principle. A common physics demonstration involves the catching of water balloons of varying speed and varying mass. A water balloon is thrown high into the air and successfully caught (i.e., caught without breaking). The key to the success of the demonstration is to contact the balloon with outstretched arms and carry the balloon for a meter or more before finally stopping its momentum. The effect of this strategy is to extend the time over which the  collision occurred and so reduce the force. This same strategy is used by lacrosse players when catching the ball. The ball is "cradled" when caught; i.e., the lacrosse player reaches out for the ball and carries it inward toward her body as if she were cradling a baby. The effect of this strategy is to lengthen the time over which the collision occurs and so reduce the force on the lacrosse ball. Now that's physics in action.
collision occurred and so reduce the force. This same strategy is used by lacrosse players when catching the ball. The ball is "cradled" when caught; i.e., the lacrosse player reaches out for the ball and carries it inward toward her body as if she were cradling a baby. The effect of this strategy is to lengthen the time over which the collision occurs and so reduce the force on the lacrosse ball. Now that's physics in action.
Another common physics demonstration involves throwing an egg into a bed sheet. The bed sheet is typically held by two trustworthy students and a volunteer is used to toss the egg at full speed into the bed sheet. The collision between the egg and the bed sheet lasts over an extended period of time since the bed sheet has some give in it. By extending the time of the collision, the effect of the force is minimized. In all my years, the egg has never broken when hitting the bed sheet. On occasion the volunteer has a wayward toss and is not as accurate as expected. The egg misses the bed sheet and collides with the wall. In these unexpected cases, the collision between wall and egg lasts for a short period of time, thus maximizing the effect of the force on the egg. The egg brakes and leaves the wall and floor in a considerable mess. And that's no yolk!
The Effect of Rebounding
Occasionally when objects collide, they bounce off each other as opposed to sticking to each other and traveling with the same speed after the collision. Bouncing off each other is known as rebounding. Rebounding involves a change in the direction of an object; the before- and after-collision direction is different. Rebounding was pictured and discussed earlier in Lesson 1. At that time, it was said that rebounding situations are characterized by a large velocity change and a large momentum change.
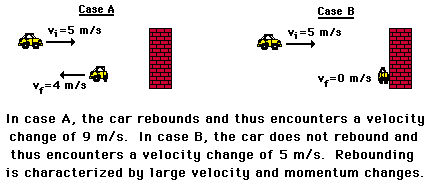
From the impulse-momentum change theorem, we could deduce that a rebounding situation must also be accompanied by a large impulse. Since the impulse experienced by an object equals the momentum change of the object, a collision characterized by a large momentum change must also be characterized by a large impulse.
The importance of rebounding is critical to the outcome of automobile accidents. In an automobile accident, two cars can either collide and bounce off each other or collide, crumple up and travel together with the same speed after the collision. But which would be more damaging to the occupants of the automobiles - the rebounding of the cars or the crumpling up of the cars? Contrary to popular opinion, the crumpling up of cars is the safest type of automobile collision. As mentioned above, if cars rebound upon collision, the momentum change will be larger and so will the impulse. A greater impulse will typically be associated with a bigger  force. Occupants of automobiles would certainly prefer small forces upon their bodies during collisions. In fact, automobile designers and safety engineers have found ways to reduce the harm done to occupants of automobiles by designing cars that crumple upon impact. Automobiles are made with crumple zones. Crumple zones are sections in cars that are designed to crumple up when the car encounters a collision. Crumple zones minimize the effect of the force in an automobile collision in two ways. By crumpling, the car is less likely to rebound upon impact, thus minimizing the momentum change and the impulse. Finally, the crumpling of the car lengthens the time over which the car's momentum is changed; by increasing the time of the collision, the force of the collision is greatly reduced.
force. Occupants of automobiles would certainly prefer small forces upon their bodies during collisions. In fact, automobile designers and safety engineers have found ways to reduce the harm done to occupants of automobiles by designing cars that crumple upon impact. Automobiles are made with crumple zones. Crumple zones are sections in cars that are designed to crumple up when the car encounters a collision. Crumple zones minimize the effect of the force in an automobile collision in two ways. By crumpling, the car is less likely to rebound upon impact, thus minimizing the momentum change and the impulse. Finally, the crumpling of the car lengthens the time over which the car's momentum is changed; by increasing the time of the collision, the force of the collision is greatly reduced.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Egg Drop Interactive. You can find it in the Physics Interactives section of our website. The
Egg Drop Interactive immerses a learner into a Virtual Egg Drop activity in order to explore the effect of drop height, egg mass, and landing surface upon the outcome of the egg.