Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 We have already learned that a lens is a carefully ground or molded piece of transparent material that refracts light rays in such a way as to form an image. Lenses serve to refract light at each boundary. As a ray of light enters a lens, it is refracted; and as the same ray of light exits the lens, it is refracted again. The net effect of the refraction of light at these two boundaries is that the light ray has changed directions. Because of the special geometric shape of a lens, the light rays are refracted such that they form images. Before we approach the topic of image formation, we will investigate the refractive ability of converging and diverging lenses.
We have already learned that a lens is a carefully ground or molded piece of transparent material that refracts light rays in such a way as to form an image. Lenses serve to refract light at each boundary. As a ray of light enters a lens, it is refracted; and as the same ray of light exits the lens, it is refracted again. The net effect of the refraction of light at these two boundaries is that the light ray has changed directions. Because of the special geometric shape of a lens, the light rays are refracted such that they form images. Before we approach the topic of image formation, we will investigate the refractive ability of converging and diverging lenses.
How a Lens Refracts Light
First lets consider a double convex lens. Suppose that several rays of light approach the lens; and suppose that these rays of light are traveling parallel to the principal axis. Upon reaching the front face of the lens, each ray of light will refract towards the normal to the surface. At this boundary, the light ray is passing from air into a more dense medium (usually plastic or glass). Since the light ray is passing from a medium in which it travels fast (less optically dense) into a medium in which it travels relatively slow (more optically dense), it will bend towards the normal line. This is the FST principle of refraction. This is shown for two incident rays on the diagram below. Once the light ray refracts across the boundary and enters the lens, it travels in a straight line until it reaches the back face of the lens. At this boundary, each ray of light will refract away from the normal to the surface. Since the light ray is passing from a medium in which it travels slow (more optically dense) to a medium in which it travels fast (less optically dense), it will bend away from the normal line; this is the SFA principle of refraction.
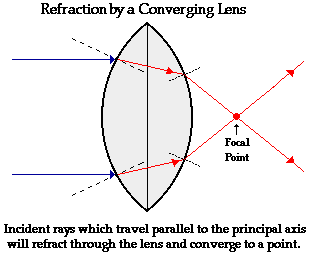
The above diagram shows the behavior of two incident rays approaching parallel to the principal axis. Note that the two rays converge at a point; this point is known as the focal point of the lens. The first generalization that can be made for the refraction of light by a double convex lens is as follows:
|
Refraction Rule for a Converging Lens
Any incident ray traveling parallel to the principal axis of a converging lens will refract through the lens and travel through the focal point on the opposite side of the lens.
|
Now suppose that the rays of light are traveling through the focal point on the way to the lens. These rays of light will refract when they enter the lens and refract when they leave the lens. As the light rays enter into the more dense lens material, they refract towards the normal; and as they exit into the less dense air, they refract away from the normal. These specific rays will exit the lens traveling parallel to the principal axis.
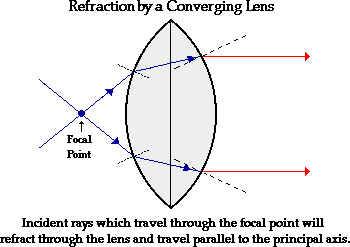
The above diagram shows the behavior of two incident rays traveling through the focal point on the way to the lens. Note that the two rays refract parallel to the principal axis. A second generalization for the refraction of light by a double convex lens can be added to the first generalization.
Refraction Rules for a Converging Lens
- Any incident ray traveling parallel to the principal axis of a converging lens will refract through the lens and travel through the focal point on the opposite side of the lens.
- Any incident ray traveling through the focal point on the way to the lens will refract through the lens and travel parallel to the principal axis.
|
The Thin Lens Approximation
These two "rules" will greatly simplify the task of determining the image location for objects placed in 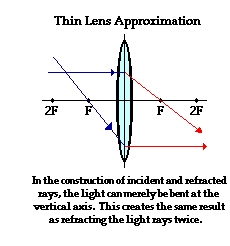 front of converging lenses. This topic will be discussed in the next part of Lesson 5. For now, internalize the meaning of the rules and be prepared to use them. As the rules are applied in the construction of ray diagrams, do not forget the fact that Snells' Law of refraction of light holds for each of these rays. It just so happens that geometrically, when Snell's Law is applied for rays that strike the lens in the manner described above, they will refract in close approximation with these two rules. The tendency of incident light rays to follow these rules is increased for lenses that are thin. For such thin lenses, the path of the light through the lens itself contributes very little to the overall change in the direction of the light rays. We will use this so-called thin-lens approximation in this unit. Furthermore, to simplify the construction of ray diagrams, we will avoid refracting each light ray twice - upon entering and emerging from the lens. Instead, we will continue the incident ray to the vertical axis of the lens and refract the light at that point. For thin lenses, this simplification will produce the same result as if we were refracting the light twice.
front of converging lenses. This topic will be discussed in the next part of Lesson 5. For now, internalize the meaning of the rules and be prepared to use them. As the rules are applied in the construction of ray diagrams, do not forget the fact that Snells' Law of refraction of light holds for each of these rays. It just so happens that geometrically, when Snell's Law is applied for rays that strike the lens in the manner described above, they will refract in close approximation with these two rules. The tendency of incident light rays to follow these rules is increased for lenses that are thin. For such thin lenses, the path of the light through the lens itself contributes very little to the overall change in the direction of the light rays. We will use this so-called thin-lens approximation in this unit. Furthermore, to simplify the construction of ray diagrams, we will avoid refracting each light ray twice - upon entering and emerging from the lens. Instead, we will continue the incident ray to the vertical axis of the lens and refract the light at that point. For thin lenses, this simplification will produce the same result as if we were refracting the light twice.
Rules of Refraction for Diverging Lenses
Now let's investigate the refraction of light by double concave lens. Suppose that several rays of light approach the lens; and suppose that these rays of light are traveling parallel to the principal axis. Upon reaching the front face of the lens, each ray of light will refract towards the normal to the surface. At this boundary, the light ray is passing from air into a more dense medium (usually plastic or glass). Since the light ray is passing from a medium in which it travels relatively fast (less optically dense) into a medium in which it travels relatively slow (more optically dense), it will bend towards the normal line. This is the FST principle of refraction. This is shown for two incident rays on the diagram below. Once the light ray refracts across the boundary and enters the lens, it travels in a straight line until it reaches the back face of the lens. At this boundary, each ray of light will refract away from the normal to the surface. Since the light ray is passing from a medium in which it travels relatively slow (more optically dense) to a medium in which it travels fast (less optically dense), it will bend away from the normal line. This is the SFA principle of refraction. These principles of refraction are identical to what was observed for the double convex lens above.
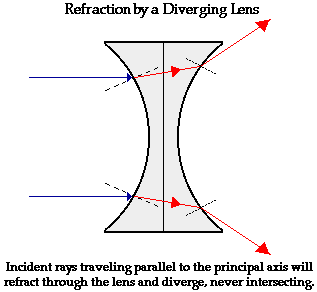
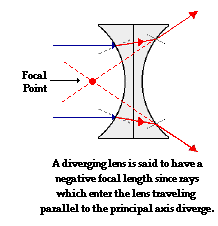 The above diagram shows the behavior of two incident rays approaching parallel to the principal axis of the double concave lens. Just like the double convex lens above, light bends towards the normal when entering and away from the normal when exiting the lens. Yet, because of the different shape of the double concave lens, these incident rays are not converged to a point upon refraction through the lens. Rather, these incident rays diverge upon refracting through the lens. For this reason, a double concave lens can never produce a real image. Double concave lenses produce images that are virtual. This will be discussed in more detail in the next part of Lesson 5. If the refracted rays are extended backwards behind the lens, an important observation is made. The extension of the refracted rays will intersect at a point. This point is known as the focal point. Notice that a diverging lens such as this double concave lens does not really focus the incident light rays that are parallel to the principal axis; rather, it diverges these light rays. For this reason, a diverging lens is said to have a negative focal length.
The above diagram shows the behavior of two incident rays approaching parallel to the principal axis of the double concave lens. Just like the double convex lens above, light bends towards the normal when entering and away from the normal when exiting the lens. Yet, because of the different shape of the double concave lens, these incident rays are not converged to a point upon refraction through the lens. Rather, these incident rays diverge upon refracting through the lens. For this reason, a double concave lens can never produce a real image. Double concave lenses produce images that are virtual. This will be discussed in more detail in the next part of Lesson 5. If the refracted rays are extended backwards behind the lens, an important observation is made. The extension of the refracted rays will intersect at a point. This point is known as the focal point. Notice that a diverging lens such as this double concave lens does not really focus the incident light rays that are parallel to the principal axis; rather, it diverges these light rays. For this reason, a diverging lens is said to have a negative focal length.
The first generalization can now be made for the refraction of light by a double concave lens:
|
Refraction Rule for a Diverging Lens
Any incident ray traveling parallel to the principal axis of a diverging lens will refract through the lens and travel in line with the focal point (i.e., in a direction such that its extension will pass through the focal point).
|
Now suppose that the rays of light are traveling towards the focal point on the way to the lens. Because of the negative focal length for double concave lenses, the light rays will head towards the focal point on the opposite side of the lens. These rays will actually reach the lens before they reach the focal point. These rays of light will refract when they enter the lens and refract when they leave the lens. As the light rays enter into the more dense lens material, they refract towards the normal; and as they exit into the less dense air, they refract away from the normal. These specific rays will exit the lens traveling parallel to the principal axis.
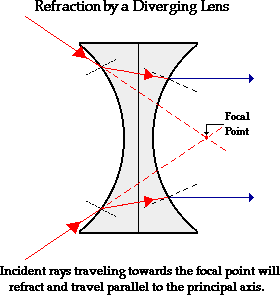
The above diagram shows the behavior of two incident rays traveling towards the focal point on the way to the lens. Note that the two rays refract parallel to the principal axis. A second generalization for the refraction of light by a double concave lens can be added to the first generalization.
Refraction Rules for a Diverging Lens
- Any incident ray traveling parallel to the principal axis of a diverging lens will refract through the lens and travel in line with the focal point (i.e., in a direction such that its extension will pass through the focal point).
- Any incident ray traveling towards the focal point on the way to the lens will refract through the lens and travel parallel to the principal axis.
|
A Third Rule of Refraction for Lenses
The above discussion focuses on the manner in which converging and diverging lenses refract incident rays that are traveling parallel to the principal axis or are traveling through (or towards) the focal point. But these are not the only two possible incident rays. There are a multitude of incident rays that strike the lens and refract in a variety of ways. Yet, there are three specific rays that behave in a very predictable manner. The third ray that we will investigate is the ray that passes through the precise center of the lens - through the point where the principal axis and the vertical axis intersect. This ray will refract as it enters and refract as it exits the lens, but the net effect of this dual refraction is that the path of the light ray is not changed. For a thin lens, the refracted ray is traveling in the same direction as the incident ray and is approximately in line with it. The behavior of this third incident ray is depicted in the diagram below.
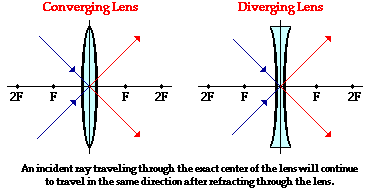
Now we have three incident rays whose refractive behavior is easily predicted. These three rays lead to our three rules of refraction for converging and diverging lenses. These three rules are summarized below.
Refraction Rules for a Converging Lens
- Any incident ray traveling parallel to the principal axis of a converging lens will refract through the lens and travel through the focal point on the opposite side of the lens.
- Any incident ray traveling through the focal point on the way to the lens will refract through the lens and travel parallel to the principal axis.
- An incident ray that passes through the center of the lens will in effect continue in the same direction that it had when it entered the lens.
|
Refraction Rules for a Diverging Lens
- Any incident ray traveling parallel to the principal axis of a diverging lens will refract through the lens and travel in line with the focal point (i.e., in a direction such that its extension will pass through the focal point).
- Any incident ray traveling towards the focal point on the way to the lens will refract through the lens and travel parallel to the principal axis.
- An incident ray that passes through the center of the lens will in effect continue in the same direction that it had when it entered the lens.
|
These three rules of refraction for converging and diverging lenses will be applied through the remainder of this lesson. The rules merely describe the behavior of three specific incident rays. While there is a multitude of light rays being captured and refracted by a lens, only two rays are needed in order to determine the image location. So as we proceed with this lesson, pick your favorite two rules (usually, the ones that are easiest to remember) and apply them to the construction of ray diagrams and the determination of the image location and characteristics.
We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Optics Bench Interactive. You can find this in the Physics Interactives section of our website. The
Optics Bench Interactive provides the learner an interactive enivronment for exploring the formation of images by lenses and mirrors. Its like having a complete optics toolkit on your screen.