 On occasion objects move within a medium that is moving with respect to an observer. For example, an airplane usually encounters a wind - air that is moving with respect to an observer on the ground below. As another example, a motorboat in a river is moving amidst a river current - water that is moving with respect to an observer on dry land. In such instances as this, the magnitude of the velocity of the moving object (whether it be a plane or a motorboat) with respect to the observer on land will not be the same as the speedometer reading of the vehicle. That is to say, the speedometer on the motorboat might read 20 mi/hr; yet the motorboat might be moving relative to the observer on shore at a speed of 25 mi/hr. Motion is relative to the observer. The observer on land, often named (or misnamed) the "stationary observer" would measure the speed to be different than that of the person on the boat. The observed speed of the boat must always be described relative to who the observer is.
On occasion objects move within a medium that is moving with respect to an observer. For example, an airplane usually encounters a wind - air that is moving with respect to an observer on the ground below. As another example, a motorboat in a river is moving amidst a river current - water that is moving with respect to an observer on dry land. In such instances as this, the magnitude of the velocity of the moving object (whether it be a plane or a motorboat) with respect to the observer on land will not be the same as the speedometer reading of the vehicle. That is to say, the speedometer on the motorboat might read 20 mi/hr; yet the motorboat might be moving relative to the observer on shore at a speed of 25 mi/hr. Motion is relative to the observer. The observer on land, often named (or misnamed) the "stationary observer" would measure the speed to be different than that of the person on the boat. The observed speed of the boat must always be described relative to who the observer is.
Tailwinds, Headwinds, and Side Winds
To illustrate this principle, consider a plane flying amidst a tailwind. A tailwind is merely a wind that approaches the plane from behind, thus increasing its resulting velocity. If the plane is traveling at a velocity of 100 km/hr with respect to the air, and if the wind velocity is 25 km/hr, then what is the velocity of the plane relative to an observer on the ground below? The resultant velocity of the plane (that is, the result of the wind velocity contributing to the velocity due to the plane's motor) is the vector sum of the velocity of the plane and the velocity of the wind. This resultant velocity is quite easily determined if the wind approaches the plane directly from behind. As shown in the diagram below, the plane travels with a resulting velocity of 125 km/hr relative to the ground.
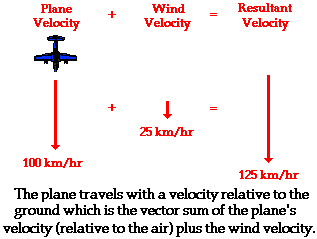
If the plane encounters a headwind, the resulting velocity will be less than 100 km/hr. Since a headwind is a wind that approaches the plane from the front, such a wind would decrease the plane's resulting velocity. Suppose a plane traveling with a velocity of 100 km/hr with respect to the air meets a headwind with a velocity of 25 km/hr. In this case, the resultant velocity would be 75 km/hr; this is the velocity of the plane relative to an observer on the ground. This is depicted in the diagram below.
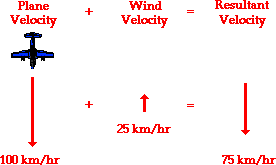
Now consider a plane traveling with a velocity of 100 km/hr, South that encounters a side wind of 25 km/hr, West. Now what would the resulting velocity of the plane be? This question can be answered in the same manner as the previous questions. The resulting velocity of the plane is the vector sum of the two individual velocities. To determine the resultant velocity, the plane velocity (relative to the air) must be added to the wind velocity. This is the same procedure that was used above for the headwind and the tailwind situations; only now, the resultant is not as easily computed. Since the two vectors to be added - the southward plane velocity and the westward wind velocity - are at right angles to each other, the Pythagorean theorem can be used. This is illustrated in the diagram below.
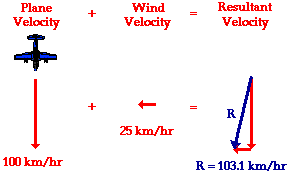
In this situation of a side wind, the southward vector can be added to the westward vector using the usual methods of vector addition. The magnitude of the resultant velocity is determined using Pythagorean theorem. The algebraic steps are as follows:
(100 km/hr)2 + (25 km/hr)2 = R2
10 000 km2/hr2 + 625 km2/hr2 = R2
10 625 km2/hr2 = R2
SQRT(10 625 km2/hr2) = R
103.1 km/hr = R
The direction of the resulting velocity can be determined using a trigonometric function. Since the plane velocity and the wind velocity form a right triangle when added together in head-to-tail fashion, the angle between the resultant vector and the southward vector can be determined using the sine, cosine, or tangent functions. The tangent  function can be used; this is shown below:
function can be used; this is shown below:
tan (theta) = (opposite/adjacent)
tan (theta) = (25/100)
theta = invtan (25/100)
theta = 14.0 degrees
If the resultant velocity of the plane makes a 14.0 degree angle with the southward direction (theta in the above diagram), then the direction of the resultant is 256 degrees. Like any vector, the resultant's direction is measured as a counterclockwise angle of rotation from due East.

Analysis of a Riverboat's Motion
The effect of the wind upon the plane is similar to the effect of the river current upon the motorboat. If a motorboat were to head straight across a river (that is, if the boat were to point its bow straight towards the other side), it would not reach the shore directly across from its starting point. The river current influences the motion of the boat and carries it downstream. The motorboat may be moving with a velocity of 4 m/s directly across the river, yet the resultant velocity of the boat will be greater than 4 m/s and at an angle in the downstream direction. While the speedometer of the boat may read 4 m/s, its speed with respect to an observer on the shore will be greater than 4 m/s.
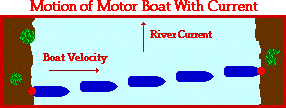
The resultant velocity of the motorboat can be determined in the same manner as was done for the plane. The resultant velocity of the boat is the vector sum of the boat velocity and the river velocity. Since the boat heads straight across the river and since the current is always directed straight downstream, the two vectors are at right angles to each other. Thus, the Pythagorean theorem can be used to determine the resultant velocity. Suppose that the river was moving with a velocity of 3 m/s, North and the motorboat was moving with a velocity of 4 m/s, East. What would be the resultant velocity of the motorboat (i.e., the velocity relative to an observer on the shore)? The magnitude of the resultant can be found as follows:
(4.0 m/s)2 + (3.0 m/s)2 = R2
16 m2/s2 + 9 m2/s2 = R2
25 m2/s2 = R2
SQRT (25 m2/s2) = R
5.0 m/s = R
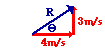 The direction of the resultant is the counterclockwise angle of rotation that the resultant vector makes with due East. This angle can be determined using a trigonometric function as shown below.
The direction of the resultant is the counterclockwise angle of rotation that the resultant vector makes with due East. This angle can be determined using a trigonometric function as shown below.
tan (theta) = (opposite/adjacent)
tan (theta) = (3/4)
theta = invtan (3/4)
theta = 36.9 degrees
Given a boat velocity of 4 m/s, East and a river velocity of 3 m/s, North, the resultant velocity of the boat will be 5 m/s at 36.9 degrees.
Motorboat problems such as these are typically accompanied by three separate questions:
- What is the resultant velocity (both magnitude and direction) of the boat?
- If the width of the river is X meters wide, then how much time does it take the boat to travel shore to shore?
- What distance downstream does the boat reach the opposite shore?
The first of these three questions was answered above; the resultant velocity of the boat can be determined using the Pythagorean theorem (magnitude) and a trigonometric function (direction). The second and third of these questions can be answered using the average speed equation (and a lot of logic).
ave. speed = distance/time
Consider the following example.
Example 1
A motorboat traveling 4 m/s, East encounters a current traveling 3.0 m/s, North.
- What is the resultant velocity of the motorboat?
- If the width of the river is 80 meters wide, then how much time does it take the boat to travel shore to shore?
- What distance downstream does the boat reach the opposite shore?
|
The solution to the first question has already been shown in the above discussion. The resultant velocity of the boat is 5 m/s at 36.9 degrees. We will start in on the second question.
The river is 80-meters wide. That is, the distance from shore to shore as measured straight across the river is 80 meters. The time to cross this 80-meter wide river can be determined by rearranging and substituting into the average speed equation.
time = distance /(ave. speed)
The distance of 80 m can be substituted into the numerator. But what about the denominator? What value should be used for average speed? Should 3 m/s (the current velocity), 4 m/s (the boat velocity), or 5 m/s (the resultant velocity) be used as the average speed value for covering the 80 meters? With what average speed is the boat traversing the 80 meter wide river? Most students want to use the resultant velocity in the equation since that is the actual velocity of the boat with respect to the shore. Yet the value of 5 m/s is the speed at which the boat covers the diagonal dimension of the river. And the diagonal distance across the river is not known in this case. If one knew the distance C in the diagram below, then the average speed C could be used to calculate the time to reach the opposite shore. Similarly, if one knew the distance B in the diagram below, then the average speed B could be used to calculate the time to reach the opposite shore. And finally, if one knew the distance A in the diagram below, then the average speed A could be used to calculate the time to reach the opposite shore.
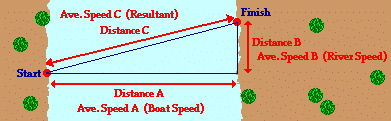
In our problem, the 80 m corresponds to the distance A, and so the average speed of 4 m/s (average speed in the direction straight across the river) should be substituted into the equation to determine the time.
time = (80 m)/(4 m/s) = 20 s
It requires 20 s for the boat to travel across the river. During this 20 s of crossing the river, the boat also drifts downstream. Part c of the problem asks "What distance downstream does the boat reach the opposite shore?" The same equation must be used to calculate this downstream distance. And once more, the question arises, which one of the three average speed values must be used in the equation to calculate the distance downstream? The distance downstream corresponds to Distance B on the above diagram. The speed at which the boat covers this distance corresponds to Average Speed B on the diagram above (i.e., the speed at which the current moves - 3 m/s). And so the average speed of 3 m/s (average speed in the downstream direction) should be substituted into the equation to determine the distance.
distance = ave. speed * time = (3 m/s) * (20 s)
distance = 60 m
The boat is carried 60 meters downstream during the 20 seconds it takes to cross the river.
The mathematics of the above problem is no more difficult than dividing or multiplying two numerical quantities by each other. The mathematics is easy! The difficulty of the problem is conceptual in nature; the difficulty lies in deciding which numbers to use in the equations. That decision emerges from one's conceptual understanding (or unfortunately, one's misunderstanding) of the complex motion that is occurring. The motion of the riverboat can be divided into two simultaneous parts - a motion in the direction straight across the river and a motion in the downstream direction. These two parts (or components) of the motion occur simultaneously for the same time duration (which was 20 seconds in the above problem). The decision as to which velocity value or distance value to use in the equation must be consistent with the diagram above. The boat's motor is what carries the boat across the river the Distance A; and so any calculation involving the Distance A must involve the speed value labeled as Speed A (the boat speed relative to the water). Similarly, it is the current of the river that carries the boat downstream for the Distance B; and so any calculation involving the Distance B must involve the speed value labeled as Speed B (the river speed). Together, these two parts (or components) add up to give the resulting motion of the boat. That is, the across-the-river component of displacement adds to the downstream displacement to equal the resulting displacement. And likewise, the boat velocity (across the river) adds to the river velocity (down the river) to equal the resulting velocity. And so any calculation of the Distance C or the Average Speed C ("Resultant Velocity") can be performed using the Pythagorean theorem.
Now to illustrate an important point, let's try a second example problem that is similar to the first example problem. Make an attempt to answer the three questions and then click the button to check your answer.
Example 2
A motorboat traveling 4 m/s, East encounters a current traveling 7.0 m/s, North.
- What is the resultant velocity of the motorboat?
- If the width of the river is 80 meters wide, then how much time does it take the boat to travel shore to shore?
- What distance downstream does the boat reach the opposite shore?
|
An important concept emerges from the analysis of the two example problems above. In Example 1, the time to cross the 80-meter wide river (when moving 4 m/s) was 20 seconds. This was in the presence of a 3 m/s current velocity. In Example 2, the current velocity was much greater - 7 m/s - yet the time to cross the river remained unchanged. In fact, the current velocity itself has no effect upon the time required for a boat to cross the river. The river moves downstream parallel to the banks of the river. As such, there is no way that the current is capable of assisting a boat in crossing a river. While the increased current may affect the resultant velocity - making the boat travel with a greater speed with respect to an observer on the ground - it does not increase the speed in the direction across the river. The component of the resultant velocity that is increased is the component that is in a direction pointing down the river. It is often said that "perpendicular components of motion are independent of each other." As applied to riverboat problems, this would mean that an across-the-river variable would be independent of (i.e., not be affected by) a downstream variable. The time to cross the river is dependent upon the velocity at which the boat crosses the river. It is only the component of motion directed across the river (i.e., the boat velocity) that affects the time to travel the distance directly across the river (80 m in this case). The component of motion perpendicular to this direction - the current velocity - only affects the distance that the boat travels down the river. This concept of perpendicular components of motion will be investigated in more detail in the next part of Lesson 1.

Check Your Understanding
1. A plane can travel with a speed of 80 mi/hr with respect to the air. Determine the resultant velocity of the plane (magnitude only) if it encounters a
a. 10 mi/hr headwind.
b. 10 mi/hr tailwind.
c. 10 mi/hr crosswind.
d. 60 mi/hr crosswind.
2. A motorboat traveling 5 m/s, East encounters a current traveling 2.5 m/s, North.
a. What is the resultant velocity of the motor boat?
b. If the width of the river is 80 meters wide, then how much time does it take the boat to travel shore to shore?
c. What distance downstream does the boat reach the opposite shore?
3. A motorboat traveling 5 m/s, East encounters a current traveling 2.5 m/s, South.
a. What is the resultant velocity of the motor boat?
b. If the width of the river is 80 meters wide, then how much time does it take the boat to travel shore to shore?
c. What distance downstream does the boat reach the opposite shore?
4. A motorboat traveling 6 m/s, East encounters a current traveling 3.8 m/s, South.
a. What is the resultant velocity of the motor boat?
b. If the width of the river is 120 meters wide, then how much time does it take the boat to travel shore to shore?
c. What distance downstream does the boat reach the opposite shore?
5. If the current velocity in question #4 were increased to 5 m/s, then
a. how much time would be required to cross the same 120-m wide river?
b. what distance downstream would the boat travel during this time?