Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
As mentioned in the previous part of this lesson, momentum is a commonly used term in sports.  When a sports announcer says that a team has the momentum they mean that the team is really on the move and is going to be hard to stop. The term momentum is a physics concept. Any object with momentum is going to be hard to stop. To stop such an object, it is necessary to apply a force against its motion for a given period of time. The more momentum that an object has, the harder that it is to stop. Thus, it would require a greater amount of force or a longer amount of time or both to bring such an object to a halt. As the force acts upon the object for a given amount of time, the object's velocity is changed; and hence, the object's momentum is changed.
When a sports announcer says that a team has the momentum they mean that the team is really on the move and is going to be hard to stop. The term momentum is a physics concept. Any object with momentum is going to be hard to stop. To stop such an object, it is necessary to apply a force against its motion for a given period of time. The more momentum that an object has, the harder that it is to stop. Thus, it would require a greater amount of force or a longer amount of time or both to bring such an object to a halt. As the force acts upon the object for a given amount of time, the object's velocity is changed; and hence, the object's momentum is changed.
 The concepts in the above paragraph should not seem like abstract information to you. You have observed this a number of times if you have watched the sport of football. In football, the defensive players apply a force for a given amount of time to stop the momentum of the offensive player who has the ball. You have also experienced this a multitude of times while driving. As you bring your car to a halt when approaching a stop sign or stoplight, the brakes serve to apply a force to the car for a given amount of time to change the car's momentum. An object with momentum can be stopped if a force is applied against it for a given amount of time.
The concepts in the above paragraph should not seem like abstract information to you. You have observed this a number of times if you have watched the sport of football. In football, the defensive players apply a force for a given amount of time to stop the momentum of the offensive player who has the ball. You have also experienced this a multitude of times while driving. As you bring your car to a halt when approaching a stop sign or stoplight, the brakes serve to apply a force to the car for a given amount of time to change the car's momentum. An object with momentum can be stopped if a force is applied against it for a given amount of time.
A force acting for a given amount of time will change an object's momentum. Put another way, an unbalanced force always accelerates an object - either speeding it up or slowing it down. If the force acts opposite the object's motion, it slows the object down. If a force acts in the same direction as the object's motion, then the force speeds the object up. Either way, a force will change the velocity of an object. And if the velocity of the object is changed, then the momentum of the object is changed.
Impulse
These concepts are merely an outgrowth of Newton's second law as discussed in an earlier unit. Newton's second law (Fnet = m • a) stated that the acceleration of an object is directly proportional to the net force acting upon the object and inversely proportional to the mass of the object. When combined with the definition of acceleration (a = change in velocity / time), the following equalities result.
F = m • a
or
F = m • ∆v / t
If both sides of the above equation are multiplied by the quantity t, a new equation results.
F • t = m • ∆v
This equation represents one of two primary principles to be used in the analysis of collisions during this unit. To truly understand the equation, it is important to understand its meaning in words. In words, it could be said that the force times the time equals the mass times the change in velocity. In physics, the quantity Force • time is known as impulse. And since the quantity m•v is the momentum, the quantity m•Δv must be the change in momentum. The equation really says that the
Impulse = Change in momentum
One focus of this unit is to understand the physics of collisions. The physics of collisions are governed by the laws of momentum; and the first law that we discuss in this unit is expressed in the above equation. The equation is known as the
impulse-momentum change equation. The law can be expressed this way:
In a collision, an object experiences a force for a specific amount of time that results in a change in momentum. The result of the force acting for the given amount of time is that the object's mass either speeds up or slows down (or changes direction). The impulse experienced by the object equals the change in momentum of the object. In equation form, F • t = m • Δ v.
In a collision, objects experience an impulse; the impulse causes and is equal to the change in momentum. Consider a football halfback running down the football field and encountering a collision with a defensive back. The collision would change the halfback's speed and thus his momentum. If the motion was represented by a ticker tape diagram, it might appear as follows:

At approximately the tenth dot on the diagram, the collision occurs and lasts for a certain amount of time; in terms of dots, the collision lasts for a time equivalent to approximately nine dots. In the halfback-defensive back collision, the halfback experiences a force that lasts for a certain amount of time to change his momentum. Since the collision causes the rightward-moving halfback to slow down, the force on the halfback must have been directed leftward. If the halfback experienced a force of 800 N for 0.9 seconds, then we could say that the impulse was 720 N•s. This impulse would cause a momentum change of 720 kg•m/s. In a collision, the impulse experienced by an object is always equal to the momentum change.
Representing a Rebounding Collision
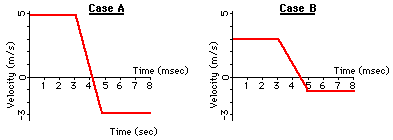
Now consider a collision of a tennis ball with a wall. Depending on the physical properties of the ball and wall, the speed at which the ball rebounds from the wall upon colliding with it will vary. The diagrams below depict the changes in velocity of the same ball. For each representation (vector diagram, velocity-time graph, and ticker tape pattern), indicate which case (A or B) has the greatest change in velocity, greatest acceleration, greatest momentum change, and greatest impulse. Support each answer. Click the button to check your answer.
Vector Diagram

|
Greatest velocity change?
|
|
Greatest acceleration?
|
|
Greatest momentum change?
|
|
Greatest Impulse?
|
Velocity-Time Graph
|
Greatest velocity change?
|
|
Greatest acceleration?
|
|
Greatest momentum change?
|
|
Greatest Impulse?
|
Ticker Tape Diagram
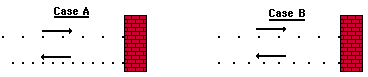
|
Greatest velocity change?
|
|
Greatest acceleration?
|
|
Greatest momentum change?
|
|
|
 Observe that each of the collisions above involve the rebound of a ball off a wall. Observe that the greater the rebound effect, the greater the acceleration, momentum change, and impulse. A rebound is a special type of collision involving a direction change in addition to a speed change. The result of the direction change is a large velocity change. On occasions in a rebound collision, an object will maintain the same or nearly the same speed as it had before the collision. Collisions in which objects rebound with the same speed (and thus, the same momentum and kinetic energy) as they had prior to the collision are known as elastic collisions. In general, elastic collisions are characterized by a large velocity change, a large momentum change, a large impulse, and a large force.
Observe that each of the collisions above involve the rebound of a ball off a wall. Observe that the greater the rebound effect, the greater the acceleration, momentum change, and impulse. A rebound is a special type of collision involving a direction change in addition to a speed change. The result of the direction change is a large velocity change. On occasions in a rebound collision, an object will maintain the same or nearly the same speed as it had before the collision. Collisions in which objects rebound with the same speed (and thus, the same momentum and kinetic energy) as they had prior to the collision are known as elastic collisions. In general, elastic collisions are characterized by a large velocity change, a large momentum change, a large impulse, and a large force.

 Use the impulse-momentum change principle to fill in the blanks in the following rows of the table. As you do, keep these three major truths in mind:
Use the impulse-momentum change principle to fill in the blanks in the following rows of the table. As you do, keep these three major truths in mind:
- The impulse experienced by an object is the force•time.
- The momentum change of an object is the mass•velocity change.
- The impulse equals the momentum change.
Click the button to view answers.
| |
Force
(N)
|
Time
(s)
|
Impulse
(N*s)
|
Mom. Change
(kg*m/s)
|
Mass
(kg)
|
Vel. Change
(m/s)
|
|
1.
|
|
0.010
|
|
|
10
|
-4
|
|
2.
|
|
0.100
|
-40
|
|
10
|
|
|
3.
|
|
0.010
|
|
-200
|
50
|
|
|
4.
|
-20 000
|
|
|
-200
|
|
-8
|
|
5.
|
-200
|
1.0
|
|
|
50
|
|
There are a few observations that can be made in the above table that relate to the computational nature of the impulse-momentum change theorem. First, observe that the answers in the table above reveal that the third and fourth columns are always equal; that is, the impulse is always equal to the momentum change. Observe also that if any two of the first three columns are known, then the remaining column can be computed. This is true because the impulse=force • time. Knowing two of these three quantities allows us to compute the third quantity. And finally, observe that knowing any two of the last three columns allows us to compute the remaining column. This is true since momentum change = mass • velocity change.
 There are also a few observations that can be made that relate to the qualitative nature of the impulse-momentum change theorem. An examination of rows 1 and 2 show that force and time are inversely proportional; for the same mass and velocity change, a tenfold increase in the time of impact corresponds to a tenfold decrease in the force of impact. An examination of rows 1 and 3 show that mass and force are directly proportional; for the same time and velocity change, a fivefold increase in the mass corresponds to a fivefold increase in the force required to stop that mass. Finally, an examination of rows 3 and 4 illustrate that mass and velocity change are inversely proportional; for the same force and time, a twofold decrease in the mass corresponds to a twofold increase in the velocity change.
There are also a few observations that can be made that relate to the qualitative nature of the impulse-momentum change theorem. An examination of rows 1 and 2 show that force and time are inversely proportional; for the same mass and velocity change, a tenfold increase in the time of impact corresponds to a tenfold decrease in the force of impact. An examination of rows 1 and 3 show that mass and force are directly proportional; for the same time and velocity change, a fivefold increase in the mass corresponds to a fivefold increase in the force required to stop that mass. Finally, an examination of rows 3 and 4 illustrate that mass and velocity change are inversely proportional; for the same force and time, a twofold decrease in the mass corresponds to a twofold increase in the velocity change.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Egg Drop Interactive. You can find it in the Physics Interactives section of our website. The
Egg Drop Interactive immerses a learner into a Virtual Egg Drop activity in order to explore the effect of drop height, egg mass, and landing surface upon the outcome of the egg.
Check Your Understanding
Express your understanding of the impulse-momentum change theorem by answering the following questions. Click the button to view the answers.
1. A 0.50-kg cart (#1) is pulled with a 1.0-N force for 1 second; another 0.50 kg cart (#2) is pulled with a 2.0 N-force for 0.50 seconds. Which cart (#1 or #2) has the greatest acceleration? Explain.
Which cart (#1 or #2) has the greatest impulse? Explain.
Which cart (#1 or #2) has the greatest change in momentum? Explain.
2. In a physics demonstration, two identical balloons (A and B) are propelled across the room on horizontal guide wires. The motion diagrams (depicting the relative position of the balloons at time intervals of 0.05 seconds) for these two balloons are shown below.

Which balloon (A or B) has the greatest acceleration? Explain.
Which balloon (A or B) has the greatest final velocity? Explain.
Which balloon (A or B) has the greatest momentum change? Explain.
Which balloon (A or B) experiences the greatest impulse? Explain.
3. Two cars of equal mass are traveling down Lake Avenue with equal velocities. They both come to a stop over different lengths of time. The ticker tape patterns for each car are shown on the diagram below.

At what approximate location on the diagram (in terms of dots) does each car begin to experience the impulse?
Which car (A or B) experiences the greatest acceleration? Explain.
Which car (A or B) experiences the greatest change in momentum? Explain.
Which car (A or B) experiences the greatest impulse? Explain.
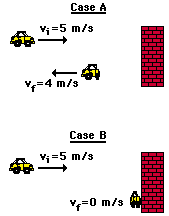 4. The diagram to the right depicts the before- and after-collision speeds of a car that undergoes a head-on-collision with a wall. In Case A, the car bounces off the wall. In Case B, the car crumples up and sticks to the wall.
4. The diagram to the right depicts the before- and after-collision speeds of a car that undergoes a head-on-collision with a wall. In Case A, the car bounces off the wall. In Case B, the car crumples up and sticks to the wall.
a. In which case (A or B) is the change in velocity the greatest? Explain.
b. In which case (A or B) is the change in momentum the greatest? Explain.
c. In which case (A or B) is the impulse the greatest? Explain.
d. In which case (A or B) is the force that acts upon the car the greatest (assume contact times are the same in both cases)? Explain.
5. Jennifer, who has a mass of 50.0 kg, is riding at 35.0 m/s in her red sports car when she must suddenly slam on the brakes to avoid hitting a deer crossing the road. She strikes the air bag, that brings her body to a stop in 0.500 s. What average force does the seat belt exert on her?
If Jennifer had not been wearing her seat belt and not had an air bag, then the windshield would have stopped her head in 0.002 s. What average force would the windshield have exerted on her?
6. A hockey player applies an average force of 80.0 N to a 0.25 kg hockey puck for a time of 0.10 seconds. Determine the impulse experienced by the hockey puck.
7. If a 5-kg object experiences a 10-N force for a duration of 0.10-second, then what is the momentum change of the object?