Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.

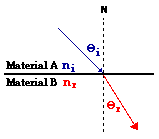
In a previous part of Lesson 2, we learned about a mathematical equation relating the two angles (angles of incidence and refraction) and the indices of refraction of the two materials on each side of the boundary. The equation is known as the Snell's Law equation and is expressed as follows.
ni • sine (Θi) = nr * sine (Θr)
where Θi ("theta i") = angle of incidence
Θr ("theta r") = angle of refraction
ni = index of refraction of the incident medium
nr = index of refraction of the refractive medium
|
|
As with any equation in physics, the Snell's Law equation is valued for its predictive ability. If any three of the four variables in the equation are known, the fourth variable can be predicted if appropriate problem-solving skills are employed. In this part of Lesson 2, we will investigate several of the types of problems that you will have to solve, and learn the task of tracing the refracted ray if given the incident ray and the indices of refraction.
Example Problem A
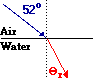
A ray of light in air is approaching the boundary with water at an angle of 52 degrees. Determine the angle of refraction of the light ray. Refer to the table of indices of refraction if necessary.
|
Solution to Problem A
The solution to this problem begins like any problem: a diagram is constructed to assist in the visualization of the physical situation, the known values are listed, and the unknown value (desired quantity) is identified. This is shown below:
|
Diagram:
|
Given:
ni = 1.00 (from table)
nr = 1.333 (from table)
Θi = 52 degrees
|
Find:
Θr =??
|
Now list the relevant equation (Snell's Law), substitute known values into the equation, and perform the proper algebraic steps to solve for the unknown.
ni • sine (Θi) = nr * sine (Θr)
1.00 * sine (52 degrees) = 1.333 * sine (Θr)
0.7880 = 1.333 * sine (Θr)
0.591 = sine (Θr)
sine-1 (0.591) = sine-1 ( sine (Θr))
36.2 degrees = Θr
Proper algebra yields the answer of 36.2 degrees for the angle of refraction. When finished, it is always a wise idea to apply the FST and SFA principles as a check of your numerical answer. In this problem, the light ray is traveling from a less optically dense or fast medium (air) into a more optically dense or slow medium (water), and so the light ray should refract towards the normal - FST. Thus, the angle of refraction should be smaller than the angle of refraction. And indeed it is - 36.2 degrees (theta r) is smaller than 52.0 degrees (theta i). Using this conceptual criterion as a check of your answer can often identify incorrect solutions to problems.
Example Problem B
A ray of light in air is approaching the boundary with a layer of crown glass at an angle of 42.0 degrees. Determine the angle of refraction of the light ray upon entering the crown glass and upon leaving the crown glass. Refer to the table of indices of refraction if necessary.
|
Solution to Problem B
This problem is slightly more complicated than Problem A since refraction is taking place at two boundaries. This is an example of a layer problem where the light refracts upon entering the layer (boundary #1: air to crown glass) and again upon leaving the layer (boundary #2: crown glass to air). Despite this complication, the solution begins like the above problem: a diagram is constructed to assist in the visualization of the physical situation, the known values are listed, and the unknown value (desired quantity) is identified. This is shown below:
|
Diagram:
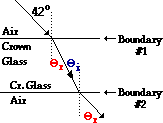
Note that the angle of
refraction at boundary #1
is the same as the angle of
incidence at boundary #2.
|
Given:
Boundary #1
ni = 1.00 (from table)
nr = 1.52 (from table)
Θi = 42.0 degrees
Boundary #2
ni = 1.52 (from table)
nr = 1.00 (from table)
|
Find:
Θr at
boundary #1
and
Θr at
boundary #2
|
Now list the relevant equation (Snell's Law), substitute known values into the equation, and perform the proper algebraic steps to solve for the unknown. Begin the process at boundary #1 and then repeat for boundary #2 until the final answer is found.
Boundary #1:
ni • sine (Θi) = nr * sine (Θr)
1.00 * sine (42.0 degrees) = 1.52 * sine (Θr)
0.669 = 1.52 * sine (Θr)
0.4402 = sine (Θr)
sine-1 (0.4402) = sine-1 ( sine (Θr))
26.1 degrees = Θr
The value of 26.1 degrees corresponds to the angle of refraction at boundary #1. Since boundary #1 is parallel to boundary #2, the angle of refraction at boundary #1 will be the same as the angle of incidence at boundary #2 (see diagram above). So now repeat the process in order to solve for the angle of refraction at boundary #2.
Boundary #2:
ni • sine (Θi) = nr * sine (Θr)
1.52 * sine (26.1 degrees) = 1.00 * sine (Θr)
1.52 * (0.4402) = 1.00 * sine (Θr)
0.6691 = sine (Θr)
sine-1 (0.6691) = sine-1 ( sine (Θr)
42.0 degrees = Θr
The answers to this problem are 26.1 degrees and 42.0 degrees.
There is an important conceptual idea that is found from an inspection of the above answer. The ray of light approached the top surface of the layer at 42 degrees and exited through the bottom surface of the layer with the same angle of 42 degrees. The light ray refracted one direction upon entering and the other direction upon exiting; the two individual effects have balanced each other and the ray is moving in the same direction. The important concept is this:
When light approaches a layer that has the shape of a parallelogram that is bounded on both sides by the same material, then the angle at which the light enters the material is equal to the angle at which light exits the layer.
If the layer is not a parallelogram or is not bound on both sides by the same material, then this will not be the case. Knowing this concept will allow you to conduct a quick check of an answer in a situation like this.
Example Problem C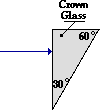
A ray of light in air is approaches a triangular piece of crown glass at an angle of 0.00 degrees (as shown in the diagram at the right). Perform the necessary calculations in order to trace the path of the light ray as it enters and exits the crown glass. Refer to the table of indices of refraction if necessary.
|
Solution to Problem C
This problem is even more complicated than Practice Problem B. Like Practice Problem B, there are two boundaries; but unlike Problem B, the two boundaries are not parallel to each other. The problem can be treated like a layer problem in which the light refracts upon entering the glass (boundary #1: air to crown glass) and upon leaving the glass (boundary #2: crown glass to air).
Despite the complication of there being nonparallel boundaries, the solution begins like the above problem: a diagram is constructed to assist in the visualization of the physical situation, the known values are listed, and the unknown value (desired quantity) is identified. This is shown below:
|
Diagram:

|
Given:
Boundary #1
ni = 1.00 (from table)
nr = 1.52 (from table)
Θi = 0.0 degrees
Boundary #2
ni = 1.52 (from table)
nr = 1.00 (from table)
|
Find:
Trace path of light.
That is, find Θr at
boundary #1
and
Θi and Θr at
boundary #2
|
Now list the relevant equation (Snell's Law), substitute known values into the equation, and perform the proper algebraic steps to solve for the unknown. Begin the process at boundary #1 and then repeat for boundary #2 until the final answer is found.
Boundary #1:
ni • sine (Θi) = nr * sine (Θr)
1.00 * sine (0.0 degrees) = 1.52 * sine (Θr)
0.000 = 1.52 * sine (Θr)
0.000 = sine (Θr)
sine-1 (0.000) = sine-1 ( sine (Θr))
0.00 degrees = Θr
This problem is made easier if you draw upon your conceptual knowledge of what occurs when a light ray approaches at an angle of incidence of 0-degrees (recall the If I Were an Archer Fish page). When approaching along the normal, the light ray passes across the boundary without refracting. If you did not know this, then you would merely recognize it upon performing your first calculation of the angle of refraction at the first boundary. The fact that the answer is 0 degrees - the same as the incident angle - means that light did not refract at this boundary.
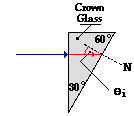 The next step demands that the light ray be traced through the triangular block until it reaches the second boundary. Draw the refracted ray at 0 degrees (i.e., trace the incident ray straight through the first boundary). At the second boundary, the normal line must be drawn (labeled N) and the angle of incidence (between the incident ray and the normal) must be measured. This is shown on the diagram at the right. The measured value of the angle of incidence at the second boundary is 30.0 degrees. This angle measurement now provides knowledge of three of the four variables in the Snell's Law equation and allows for the determination of the fourth variable (the angle of refraction) at the second boundary.
The next step demands that the light ray be traced through the triangular block until it reaches the second boundary. Draw the refracted ray at 0 degrees (i.e., trace the incident ray straight through the first boundary). At the second boundary, the normal line must be drawn (labeled N) and the angle of incidence (between the incident ray and the normal) must be measured. This is shown on the diagram at the right. The measured value of the angle of incidence at the second boundary is 30.0 degrees. This angle measurement now provides knowledge of three of the four variables in the Snell's Law equation and allows for the determination of the fourth variable (the angle of refraction) at the second boundary.
(Note: the given angle measures for the 30-60-90 degree triangle can be used along with the fact that any three angles of a triangle add to 180 degrees in order to geometrically determine this angle measure.)
Boundary #2:
ni • sine (Θi) = nr * sine (Θr)
1.52 * sine (30.0 degrees) = 1.00 * sine (Θr)
1.52 * (0.5000) = 1.00 * sine (Θr)
0.7600 = sine (Θr)
sine-1 (0.7600) = sine-1 ( sine (Θr))
49.5 degrees = Θr
 The refracted ray at the second boundary will exit at an angle of 49.5 degrees from the normal. This can be measured on the diagram and drawn with a straight edge as shown in the diagram at the right.
The refracted ray at the second boundary will exit at an angle of 49.5 degrees from the normal. This can be measured on the diagram and drawn with a straight edge as shown in the diagram at the right.
The above three practice problems demonstrate a sampling of the variety of problems that could be encountered. In the next part of Lesson 2, we will see one more type of problem.
We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Refraction Interactive. You can find it in the Physics Interactives section of our website. The
Refraction Interactive provides the learner an interactive enivronment for exploring the refraction and reflection of light at a boundary between two materials.
Check Your Understanding
1. Determine the angle of refraction for the following two refraction problems.
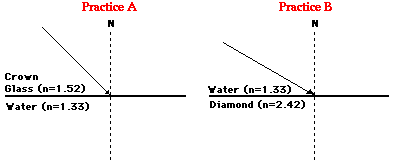
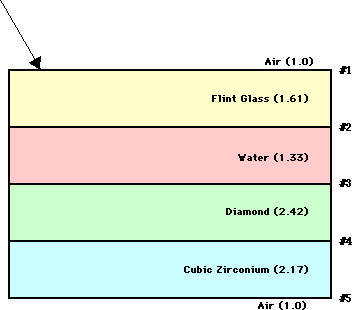
2. Perform the necessary calculations at each boundary in order to trace the path of the light ray through the following series of layers. Use a protractor and a ruler and show all your work.
3. A ray of light in crown glass exits into air at an angle of 25.0 degrees. Determine the angle at which the light approached the glass-air boundary. Refer to the table of indices of refraction if necessary.
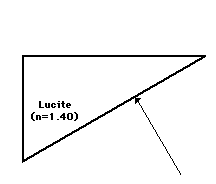
4. A ray of light is traveling through air (n = 1.00) towards a Lucite block (n = 1.40) in the shape of a 30-60-90 triangle. Trace the path of the light ray through the Lucite block shown in the diagram below.