Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 It has already been stated and thoroughly discussed that the horizontal and vertical motions of a projectile are independent of each other. The horizontal velocity of a projectile does not affect how far (or how fast) a projectile falls vertically. Perpendicular components of motion are independent of each other. Thus, an analysis of the motion of a projectile demands that the two components of motion are analyzed independent of each other, being careful not to mix horizontal motion information with vertical motion information. That is, if analyzing the motion to determine the vertical displacement, one would use kinematic equations with vertical motion parameters (initial vertical velocity, final vertical velocity, vertical acceleration) and not horizontal motion parameters (initial horizontal velocity, final horizontal velocity, horizontal acceleration). It is for this reason that one of the initial steps of a projectile motion problem is to determine the components of the initial velocity.
It has already been stated and thoroughly discussed that the horizontal and vertical motions of a projectile are independent of each other. The horizontal velocity of a projectile does not affect how far (or how fast) a projectile falls vertically. Perpendicular components of motion are independent of each other. Thus, an analysis of the motion of a projectile demands that the two components of motion are analyzed independent of each other, being careful not to mix horizontal motion information with vertical motion information. That is, if analyzing the motion to determine the vertical displacement, one would use kinematic equations with vertical motion parameters (initial vertical velocity, final vertical velocity, vertical acceleration) and not horizontal motion parameters (initial horizontal velocity, final horizontal velocity, horizontal acceleration). It is for this reason that one of the initial steps of a projectile motion problem is to determine the components of the initial velocity.
Determining the Components of a Velocity Vector
Earlier in this unit, the method of vector resolution was discussed. Vector resolution is the method of taking a single vector at an angle and separating it into two perpendicular parts. The two parts of a vector are known as components and describe the influence of that vector in a single direction. If a projectile is launched at an angle to the horizontal, then the initial velocity of the projectile has both a horizontal and a vertical component. The horizontal velocity component (vx) describes the influence of the velocity in displacing the projectile horizontally. The vertical velocity component (vy) describes the influence of the velocity in displacing the projectile vertically. Thus, the analysis of projectile motion problems begins by using the trigonometric methods discussed earlier to determine the horizontal and vertical components of the initial velocity.
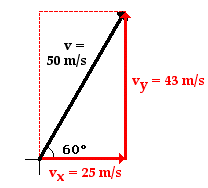
Consider a projectile launched with an initial velocity of 50 m/s at an angle of 60 degrees above the horizontal. Such a projectile begins its motion with a horizontal velocity of 25 m/s and a vertical velocity of 43 m/s. These are known as the horizontal and vertical components of the initial velocity. These numerical values were determined by constructing a sketch of the velocity vector with the given direction and then using trigonometric functions to determine the sides of the velocity triangle. The sketch is shown at the right and the use of trigonometric functions to determine the magnitudes is shown below. (If necessary, review this method on an earlier page in this unit.)
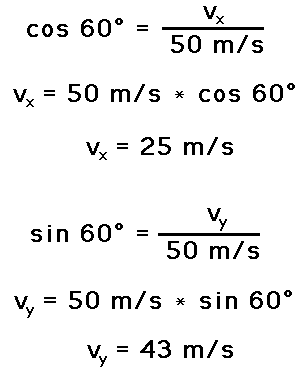
 All vector resolution problems can be solved in a similar manner. As a test of your understanding, utilize trigonometric functions to determine the horizontal and vertical components of the following initial velocity values. When finished, click the button to check your answers.
All vector resolution problems can be solved in a similar manner. As a test of your understanding, utilize trigonometric functions to determine the horizontal and vertical components of the following initial velocity values. When finished, click the button to check your answers.
Practice A: A water balloon is launched with a speed of 40 m/s at an angle of 60 degrees to the horizontal.
Practice B: A motorcycle stunt person traveling 70 mi/hr jumps off a ramp at an angle of 35 degrees to the horizontal.
Practice C: A springboard diver jumps with a velocity of 10 m/s at an angle of 80 degrees to the horizontal.
Try Some More!
Need more practice? Use the Velocity Components for a Projectile widget below to try some additional problems. Enter any velocity magnitude and angle with the horizontal. Use your calculator to determine the values of vx and vy. Then click the Submit button to check your answers.
As mentioned above, the point of resolving an initial velocity vector into its two components is to use the values of these two components to analyze a projectile's motion and determine such parameters as the horizontal displacement, the vertical displacement, the final vertical velocity, the time to reach the peak of the trajectory, the time to fall to the ground, etc. This process is demonstrated on the remainder of this page. We will begin with the determination of the time.
Determination of the Time of Flight
 The time for a projectile to rise vertically to its peak (as well as the time to fall from the peak) is dependent upon vertical motion parameters. The process of rising vertically to the peak of a trajectory is a vertical motion and is thus dependent upon the initial vertical velocity and the vertical acceleration (g = 9.8 m/s/s, down). The process of determining the time to rise to the peak is an easy process - provided that you have a solid grasp of the concept of acceleration. When first introduced, it was said that acceleration is the rate at which the velocity of an object changes. An acceleration value indicates the amount of velocity change in a given interval of time. To say that a projectile has a vertical acceleration of -9.8 m/s/s is to say that the vertical velocity changes by 9.8 m/s (in the - or downward direction) each second. For example, if a projectile is moving upwards with a velocity of 39.2 m/s at 0 seconds, then its velocity will be 29.4 m/s after 1 second, 19.6 m/s after 2 seconds, 9.8 m/s after 3 seconds, and 0 m/s after 4 seconds. For such a projectile with an initial vertical velocity of 39.2 m/s, it would take 4 seconds for it to reach the peak where its vertical velocity is 0 m/s. With this notion in mind, it is evident that the time for a projectile to rise to its peak is a matter of dividing the vertical component of the initial velocity (viy) by the acceleration of gravity.
The time for a projectile to rise vertically to its peak (as well as the time to fall from the peak) is dependent upon vertical motion parameters. The process of rising vertically to the peak of a trajectory is a vertical motion and is thus dependent upon the initial vertical velocity and the vertical acceleration (g = 9.8 m/s/s, down). The process of determining the time to rise to the peak is an easy process - provided that you have a solid grasp of the concept of acceleration. When first introduced, it was said that acceleration is the rate at which the velocity of an object changes. An acceleration value indicates the amount of velocity change in a given interval of time. To say that a projectile has a vertical acceleration of -9.8 m/s/s is to say that the vertical velocity changes by 9.8 m/s (in the - or downward direction) each second. For example, if a projectile is moving upwards with a velocity of 39.2 m/s at 0 seconds, then its velocity will be 29.4 m/s after 1 second, 19.6 m/s after 2 seconds, 9.8 m/s after 3 seconds, and 0 m/s after 4 seconds. For such a projectile with an initial vertical velocity of 39.2 m/s, it would take 4 seconds for it to reach the peak where its vertical velocity is 0 m/s. With this notion in mind, it is evident that the time for a projectile to rise to its peak is a matter of dividing the vertical component of the initial velocity (viy) by the acceleration of gravity.
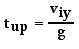
Once the time to rise to the peak of the trajectory is known, the total time of flight can be determined. For a projectile that lands at the same height which it started, the total time of flight is twice the time to rise to the peak. Recall from the last section of Lesson 2 that the trajectory of a projectile is symmetrical about the peak. That is, if it takes 4 seconds to rise to the peak, then it will take 4 seconds to fall from the peak; the total time of flight is 8 seconds. The time of flight of a projectile is twice the time to rise to the peak.
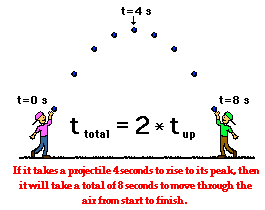
Determination of Horizontal Displacement
The horizontal displacement of a projectile is dependent upon the horizontal component of the initial velocity. As discussed in the previous part of this lesson, the horizontal displacement of a projectile can be determined using the equation
x = vix • t
If a projectile has a time of flight of 8 seconds and a horizontal velocity of 20 m/s, then the horizontal displacement is 160 meters (20 m/s • 8 s). If a projectile has a time of flight of 8 seconds and a horizontal velocity of 34 m/s, then the projectile has a horizontal displacement of 272 meters (34 m/s • 8 s). The horizontal displacement is dependent upon the only horizontal parameter that exists for projectiles - the horizontal velocity (vix).
Determination of the Peak Height
A non-horizontally launched projectile with an initial vertical velocity of 39.2 m/s will reach its peak in 4 seconds. The process of rising to the peak is a vertical motion and is again dependent upon vertical motion parameters (the initial vertical velocity and the vertical acceleration). The height of the projectile at this peak position can be determined using the equation
y = viy • t + 0.5 • g • t2
where viy is the initial vertical velocity in m/s, g is the acceleration of gravity (-9.8 m/s/s) and t is the time in seconds it takes to reach the peak. This equation can be successfully used to determine the vertical displacement of the projectile through the first half of its trajectory (i.e., peak height) provided that the algebra is properly performed and the proper values are substituted for the given variables. Special attention should be given to the facts that the t in the equation is the time up to the peak and the g has a negative value of -9.8 m/s/s.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Projectile Motion Simulator. You can find it in the Physics Interactives section of our website. The simulator allows one to explore projectile motion concepts in an interactive manner. Change a height, change an angle, change a speed, and launch the projectile.
Check Your Understanding
Answer the following questions and click the button to see the answers.
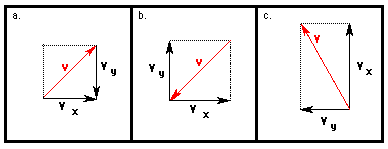
1. Aaron Agin is resolving velocity vectors into horizontal and vertical components. For each case, evaluate whether Aaron's diagrams are correct or incorrect. If incorrect, explain the problem or make the correction.
2. Use trigonometric functions to resolve the following velocity vectors into horizontal and vertical components. Then utilize kinematic equations to calculate the other motion parameters. Be careful with the equations; be guided by the principle that "perpendicular components of motion are independent of each other."
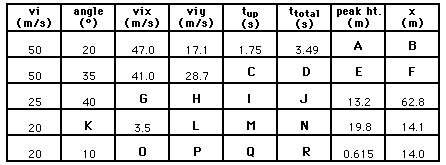
3. Utilize kinematic equations and projectile motion concepts to fill in the blanks in the following tables.