Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 In a previous part of Lesson 1, work was described as taking place when a force acts upon an object to cause a displacement. When a force acts to cause an object to be displaced, three quantities must be known in order to calculate the work. Those three quantities are force, displacement and the angle between the force and the displacement. The work is subsequently calculated as force•displacement•cosine(theta) where theta is the angle between the force and the displacement vectors. In this part of Lesson 1, the concepts and mathematics of work will be applied in order to analyze a variety of physical situations.
In a previous part of Lesson 1, work was described as taking place when a force acts upon an object to cause a displacement. When a force acts to cause an object to be displaced, three quantities must be known in order to calculate the work. Those three quantities are force, displacement and the angle between the force and the displacement. The work is subsequently calculated as force•displacement•cosine(theta) where theta is the angle between the force and the displacement vectors. In this part of Lesson 1, the concepts and mathematics of work will be applied in order to analyze a variety of physical situations.
Check Your Understanding
Express your understanding of the concept and mathematics of work by answering the following questions. When done, click the button to view the answers.
1. Apply the work equation to determine the amount of work done by the applied force in each of the three situations described below.
2. On many occasions, there is more than one force acting upon an object. A free-body diagram is a diagram that depicts the type and the direction of all the forces acting upon an object. The following descriptions and their accompanying free-body diagrams show the forces acting upon an object. For each case, indicate which force(s) are doing work upon the object. Then calculate the work done by these forces.
|
Free-Body
Diagram
|
Forces Doing Work
on the Object
|
Amount of Work Done
by Each Force
|
|
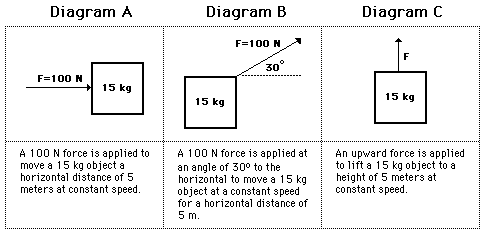
A 10-N force is applied to push a block across a friction free surface for a displacement of 5.0 m to the right.
|
|
|
|
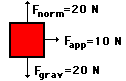
A 10-N frictional force slows a moving block to a stop after a displacement of 5.0 m to the right.
|
|
|
|
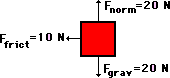
A 10-N force is applied to push a block across a frictional surface at constant speed for a displacement of 5.0 m to the right.
|
|
|
|
An approximately 2-kg object is sliding at constant speed across a friction free surface for a displacement of 5 m to the right.
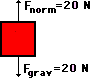
|
|
|
|
An approximately 2-kg object is pulled upward at constant speed by a 20-N force for a vertical displacement of 5 m.
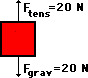
|
|
|
3. Before beginning its initial descent, a roller coaster car is always pulled up the first hill to a high initial height. Work is done on the car (usually by a chain) to achieve this initial height. A coaster designer is considering three different incline angles at which to drag the 2000-kg car train to the top of the 60-meter high hill. In each case, the force applied to the car will be applied parallel to the hill. Her critical question is: which angle would require the most work? Analyze the data, determine the work done in each case, and answer this critical question.
| |
Angle
|
Force
|
Distance
|
Work (J)
|
|
a.
|
35 deg
|
1.12 x 104 N
|
105 m
|

|
|
b.
|
45 deg
|
1.39 x 104 N
|
84.9 m
|
|
|
c.
|
55 deg
|
1.61 x 104 N
|
73.2 m
|
|
4. Ben Travlun carries a 200-N suitcase up three flights of stairs (a height of 10.0 m) and then pushes it with a horizontal force of 50.0 N at a constant speed of 0.5 m/s for a horizontal distance of 35.0 meters. How much work does Ben do on his suitcase during this entire motion?
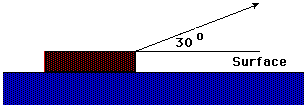
5. A force of 50 N acts on the block at the angle shown in the diagram. The block moves a horizontal distance of 3.0 m. How much work is done by the applied force?
6. How much work is done by an applied force to lift a 15-Newton block 3.0 meters vertically at a constant speed?
7. A student with a mass of 80.0 kg runs up three flights of stairs in 12.0 sec. The student has gone a vertical distance of 8.0 m. Determine the amount of work done by the student to elevate his body to this height. Assume that his speed is constant.
|
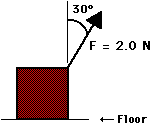
8. Calculate the work done by a 2.0-N force (directed at a 30° angle to the vertical) to move a 500 gram box a horizontal distance of 400 cm across a rough floor at a constant speed of 0.5 m/s. (HINT: Be cautious with the units.)
|
|
9. A tired squirrel (mass of 1 kg) does push-ups by applying a force to elevate its center-of-mass by 5 cm. Estimate the number of push-ups that a tired squirrel must do in order to do a approximately 5.0 Joules of work.
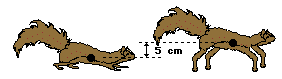
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
It's All Uphill Interactive. You can find it in the Physics Interactives section of our website. The
It's All Uphill Interactive allows a learner to explore the effect of an incline angle upon the force and the work done in pulling a cart up a hill at a constant speed.