Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 In the previous part of this lesson, the use of ray diagrams were introduced and illustrated. Ray diagrams can be used to determine where a person must sight along a mirror in order to see an image of him/herself. As such, ray diagrams can be used to determine what portion of a plane mirror must be used in order to view an image. The diagram below depicts a 6-foot tall man standing in front of a plane mirror. To see the image of his feet, he must sight along a line towards his feet; and to see the image of the top of his head, he must sight along a line towards the top of his head. The ray diagram depicts these lines of sight and the complete path of light from his extremities to the mirror and to the eye. In order to view his image, the man must look as low as point Y (to see his feet) and as high as point X (to see the tip of his head). The man only needs the portion of mirror extending between points X and Y in order to view his entire image. All other portions of the mirror are useless to the task of this man viewing his own image.
In the previous part of this lesson, the use of ray diagrams were introduced and illustrated. Ray diagrams can be used to determine where a person must sight along a mirror in order to see an image of him/herself. As such, ray diagrams can be used to determine what portion of a plane mirror must be used in order to view an image. The diagram below depicts a 6-foot tall man standing in front of a plane mirror. To see the image of his feet, he must sight along a line towards his feet; and to see the image of the top of his head, he must sight along a line towards the top of his head. The ray diagram depicts these lines of sight and the complete path of light from his extremities to the mirror and to the eye. In order to view his image, the man must look as low as point Y (to see his feet) and as high as point X (to see the tip of his head). The man only needs the portion of mirror extending between points X and Y in order to view his entire image. All other portions of the mirror are useless to the task of this man viewing his own image.
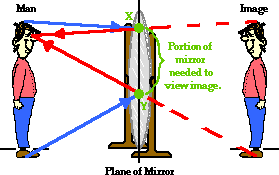
The diagram depicts some important information about plane mirrors. Using a cm-ruler, measure the height of the man (the vertical arrow) on the computer screen and measure the distance between points X and Y. What do you notice? The man is twice as tall as the distance between points X and Y. In other words, to view an image of yourself in a plane mirror, you will need an amount of mirror equal to one-half of your height. A 6-foot tall man needs 3-feet of mirror (positioned properly) in order to view his entire image.
What is the Effect of Varying Object Distance?
But what if the man stood a different distance from the mirror? Wouldn't that cause the man to need a different amount of mirror to view his image? Maybe less mirror would be required in such an instance? These questions can be explored with the help of another ray diagram. The diagram below depicts a man standing different distances from a plane mirror. Ray diagrams for each situation (standing close and standing far away) are drawn. To assist in distinguishing between the two ray diagrams, they have been color-coded. Red and blue light rays have been used for the situation in which the man is standing far away. Green and purple light rays have been used for the situation in which the man is standing close to the mirror.
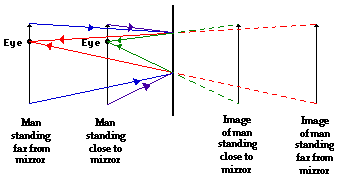
The two ray diagrams above demonstrate that the distance that a person stands from the mirror will not affect the amount of mirror that the person needs to see their image. Indeed in the diagram, the man's line of sight crosses the mirror at the same locations. A 6-foot tall man needs 3-feet of mirror to view his whole image regardless of where he is standing. In fact, the man needs the exact same 3-feet of mirror.
A common Physics lab involves using a tall plane mirror to explore the relationship between object height and the portion of mirror needed to view an image. A student stands a few meters from a plane mirror and views her image. With the student standing upright and still and staring at her feet, the lab partner moves a marker up and down the mirror until the sight location on the mirror is identified. The partner then marks this location on the mirror with an erasable marker. The process is repeated for the student staring at the tip of her head. Of course, being a lab, the procedure is subject to a variety of procedural and measurement error that may yield less than ideal results. The mirrors are occasionally mounted on a wall that is not perfectly vertical. Or a student will lean forward a slight amount, thus reducing his/her effective height. Or the mirror warps over the years leading to one that is concave or convex rather than planar. Despite these potential complications, the 1:2 ratio between the amount of mirror required to view the image and the height of the object is often observed.
We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Who Can See Who? Interactive. You can find this in the Physics Interactives section of our website. The
Who Can See Who? Interactive provides learners with an intensive mental workout in determining who can see who when looking int a plane mirror.
Check Your Understanding
1. Ben Phooled is 6-feet tall. He is the tallest person in his family. It just so happens that Ben learned the important principle of the 2:1 relationship just prior to his family's decision to purchase a mirror that was to be used by the entire family. Enthused about the recent physics lesson, Ben decided to put it to good use. Ben convinced his parents that it would be a waste of money to buy a mirror longer than 3 feet. "After all," Ben argued, "I'm the tallest person in the family and only three feet of mirror would be required to view my image." Ben's parents conceded and they purchased a 3-foot tall mirror and mounted it on the bathroom wall.
Comment on the wisdom behind the Phooled family decision.