 Ray diagrams can be used to determine the image location, size, orientation and type of image formed of objects when placed at a given location in front of a lens. The use of these diagrams was demonstrated earlier in Lesson 5 for both converging and diverging lenses. Ray diagrams provide useful information about object-image relationships, yet fail to provide the information in a quantitative form. While a ray diagram may help one determine the approximate location and size of the image, it will not provide numerical information about image distance and image size. To obtain this type of numerical information, it is necessary to use the Lens Equation and the Magnification Equation. The lens equation expresses the quantitative relationship between the object distance (do), the image distance (di), and the focal length (f). The equation is stated as follows:
Ray diagrams can be used to determine the image location, size, orientation and type of image formed of objects when placed at a given location in front of a lens. The use of these diagrams was demonstrated earlier in Lesson 5 for both converging and diverging lenses. Ray diagrams provide useful information about object-image relationships, yet fail to provide the information in a quantitative form. While a ray diagram may help one determine the approximate location and size of the image, it will not provide numerical information about image distance and image size. To obtain this type of numerical information, it is necessary to use the Lens Equation and the Magnification Equation. The lens equation expresses the quantitative relationship between the object distance (do), the image distance (di), and the focal length (f). The equation is stated as follows:
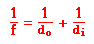
The magnification equation relates the ratio of the image distance and object distance to the ratio of the image height (hi) and object height (ho). The magnification equation is stated as follows:
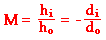
These two equations can be combined to yield information about the image distance and image height if the object distance, object height, and focal length are known.
Practice Problems
As a demonstration of the effectiveness of the lens equation and magnification equation, consider the following sample problem and its solution.
Sample Problem #1
A 4.00-cm tall light bulb is placed a distance of 45.7 cm from a double convex lens having a focal length of 15.2 cm. Determine the image distance and the image size.
Like all problems in physics, begin by the identification of the known information.
|
ho = 4.00 cm
|
do = 45.7 cm
|
f = 15.2 cm
|
Next identify the unknown quantities that you wish to solve for.
To determine the image distance, the lens equation must be used. The following lines represent the solution to the image distance; substitutions and algebraic steps are shown.
1/f = 1/do + 1/di
1/(15.2 cm) = 1/(45.7 cm) + 1/di
0.0658 cm-1 = 0.0219 cm-1 + 1/di
0.0439 cm-1 = 1/di
The numerical values in the solution above were rounded when written down, yet unrounded numbers were used in all calculations. The final answer is rounded to the third significant digit.
To determine the image height, the magnification equation is needed. Since three of the four quantities in the equation (disregarding the M) are known, the fourth quantity can be calculated. The solution is shown below.
hi/ho = - di/do
hi /(4.00 cm) = - (22.8 cm)/(45.7 cm)
hi = - (4.00 cm) • (22.8 cm)/(45.7 cm)
The negative values for image height indicate that the image is an inverted image. As is often the case in physics, a negative or positive sign in front of the numerical value for a physical quantity represents information about direction. In the case of the image height, a negative value always indicates an inverted image.
From the calculations in this problem it can be concluded that if a 4.00-cm tall object is placed 45.7 cm from a double convex lens having a focal length of 15.2 cm, then the image will be inverted, 1.99-cm tall and located 22.8 cm from the lens. The results of this calculation agree with the principles discussed earlier in this lesson. In this case, the object is located beyond the 2F point (which would be two focal lengths from the lens) and the image is located between the 2F point and the focal point. This falls into the category of Case 1: The object is located beyond 2F for a converging lens.
Now lets try a second sample problem:
Sample Problem #2
A 4.00-cm tall light bulb is placed a distance of 8.30 cm from a double convex lens having a focal length of 15.2 cm. (NOTE: this is the same object and the same lens, only this time the object is placed closer to the lens.) Determine the image distance and the image size.
Again, begin by the identification of the known information.
|
ho = 4.00 cm
|
do = 8.3 cm
|
f = 15.2 cm
|
Next identify the unknown quantities that you wish to solve for.
To determine the image distance, the lens equation will have to be used. The following lines represent the solution to the image distance; substitutions and algebraic steps are shown.
1/f = 1/do + 1/di
1/(15.2 cm) = 1/(8.30 cm) + 1/di
0.0658 cm-1 = 0.120 cm-1 + 1/di
-0.0547 cm-1 = 1/di
The numerical values in the solution above were rounded when written down, yet unrounded numbers were used in all calculations. The final answer is rounded to the third significant digit.
To determine the image height, the magnification equation is needed. Since three of the four quantities in the equation (disregarding the M) are known, the fourth quantity can be calculated. The solution is shown below.
hi/ho = - di/do
hi /(4.00 cm) = - (-18.3 cm)/(8.30 cm)
hi = - (4.00 cm) • (-18.3 cm)/(8.30 cm)
The negative value for image distance indicates that the image is a virtual image located on the object's side of the lens. Again, a negative or positive sign in front of the numerical value for a physical quantity represents information about direction. In the case of the image distance, a negative value always means the image is located on the object's side of the lens. Note also that the image height is a positive value, meaning an upright image. Any image that is upright and located on the object's side of the lens is considered to be a virtual image.
From the calculations in the second sample problem it can be concluded that if a 4.00-cm tall object is placed 8.30 cm from a double convex lens having a focal length of 15.2 cm, then the image will be enlarged, upright, 8.81-cm tall and located 18.3 cm from the lens on the object's side. The results of this calculation agree with the principles discussed earlier in this lesson. In this case, the object is located in front of the focal point (i.e., the object distance is less than the focal length) and the image is located behind the lens. This falls into the category of Case 5: The object is located in front of F (for a converging lens).
The third sample problem will pertain to a diverging lens.
Sample Problem #3
A 4.00-cm tall light bulb is placed a distance of 35.5 cm from a diverging lens having a focal length of -12.2 cm. Determine the image distance and the image size.
Like all problems in physics, begin by the identification of the known information.
|
ho = 4.00 cm
|
do = 35.5 cm
|
f = -12.2 cm
|
Next identify the unknown quantities that you wish to solve for.
To determine the image distance, the lens equation will have to be used. The following lines represent the solution to the image distance; substitutions and algebraic steps are shown.
1/f = 1/do + 1/di
1/(-12.2 cm) = 1/(35.5 cm) + 1/di
-0.0820 cm-1 = 0.0282 cm-1 + 1/di
-0.110 cm-1 = 1/di
The numerical values in the solution above were rounded when written down, yet unrounded numbers were used in all calculations. The final answer is rounded to the third significant digit.
To determine the image height, the magnification equation is needed. Since three of the four quantities in the equation (disregarding the M) are known, the fourth quantity can be calculated. The solution is shown below.
hi/ho = - di/do
hi /(4.00 cm) = - (-9.08 cm)/(35.5 cm)
hi = - (4.00 cm) * (-9.08 cm)/(35.5 cm)
The negative values for image distance indicate that the image is located on the object's side of the lens. As mentioned, a negative or positive sign in front of the numerical value for a physical quantity represents information about direction. In the case of the image distance, a negative value always indicates the existence of a virtual image located on the object's side of the lens. In the case of the image height, a positive value indicates an upright image.
From the calculations in this problem it can be concluded that if a 4.00-cm tall object is placed 35.5 cm from a diverging lens having a focal length of 12.2 cm, then the image will be upright, 1.02-cm tall and located 9.08 cm from the lens on the object's side. The results of this calculation agree with the principles discussed earlier in this lesson. Diverging lenses always produce images that are upright, virtual, reduced in size, and located on the object's side of the lens.
Practice Makes Perfect!
Use the Find the Image Distance widget below to investigate the effect of focal length and object distance upon the image distance. Simply enter the focal length and the object distance. Then click the Calculate Image Distance button to view the result. Use the widget as a practice tool.
A constant challenge of photographers is to produce an image in which as much of the subject is focused as possible. Digital cameras use lenses to focus an image on the sensing plate, the same distance from the lens. Yet we have learned in this lesson that the image distance varies with object distance. So how can a photographer focus objects within the field of view if they are varying distances from the camera? This is a constant challenge for photographers (whether amateur enthusiasts or professional) who wish to controle how much of the subject is focused. Depth of field is the photographer's term to describe the distance from the nearest to the farthest object in the field of view that are acceptably focused within the photograph. The Photography and Depth of Field widget allows you to explore the variables affecting the depth of field.
The f-stop or f-number of a camera lens is related to the size of the circular opening or aperture through which light passes on its way to the digital sensor. The greater the f-number, the smaller the opening and the less light that gets through to the sensor. The circle of confusion is related to the limitation of the eye to resolve the detail of an image within a small region. For a 35-mm camera whose images are enlarged to a 5"x7" print, the generally accepted circle of confusion value is 0.0333 mm.
Sign Conventions
The sign conventions for the given quantities in the lens equation and magnification equations are as follows:
- f is + if the lens is a double convex lens (converging lens)
- f is - if the lens is a double concave lens (diverging lens)
- di is + if the image is a real image and located on the opposite side of the lens.
- di is - if the image is a virtual image and located on the object's side of the lens.
- hi is + if the image is an upright image (and therefore, also virtual)
- hi is - if the image an inverted image (and therefore, also real)
Like many mathematical problems in physics, the skill is only acquired through much personal practice. Perhaps you would like to take some time to try the following problems.
We Would Like to Suggest ...

Why just read about it and when you could be interacting with it? Interact - that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of our
Optics Bench Interactive. You can find this in the Physics Interactives section of our website. The
Optics Bench Interactive provides the learner an interactive enivronment for exploring the formation of images by lenses and mirrors. Its like having a complete optics toolkit on your screen.
Check Your Understanding
1. Determine the image distance and image height for a 5-cm tall object placed 45.0 cm from a double convex lens having a focal length of 15.0 cm.
2. Determine the image distance and image height for a 5-cm tall object placed 30.0 cm from a double convex lens having a focal length of 15.0 cm.
3. Determine the image distance and image height for a 5-cm tall object placed 20.0 cm from a double convex lens having a focal length of 15.0 cm.
4. Determine the image distance and image height for a 5-cm tall object placed 10.0 cm from a double convex lens having a focal length of 15.0 cm.
5. A magnified, inverted image is located a distance of 32.0 cm from a double convex lens with a focal length of 12.0 cm. Determine the object distance and tell whether the image is real or virtual.
6. ZINGER: An inverted image is magnified by 2 when the object is placed 22 cm in front of a double convex lens. Determine the image distance and the focal length of the lens.
7. A double concave lens has a focal length of -10.8 cm. An object is placed 32.7 cm from the lens's surface. Determine the image distance.
8. Determine the focal length of a double concave lens that produces an image that is 16.0 cm behind the lens when the object is 28.5 cm from the lens.
9. A 2.8-cm diameter coin is placed a distance of 25.0 cm from a double concave lens that has a focal length of -12.0 cm. Determine the image distance and the diameter of the image.
10. The focal point is located 20.0 cm from a double concave lens. An object is placed 12 cm from the lens. Determine the image distance.