Energy Transformation for Downhill Skiing
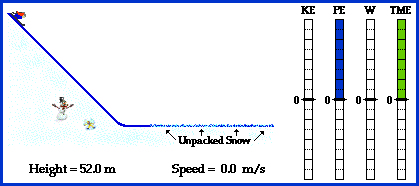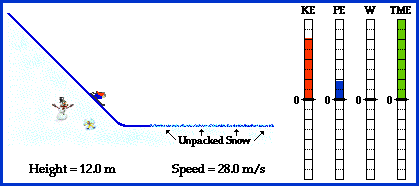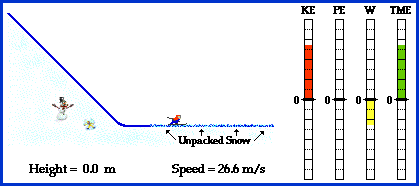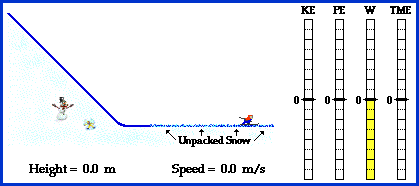
Downhill skiing is a classic illustration of the relationship between work and energy. The skier begins at an elevated position, thus possessing a large quantity of potential energy (i.e., energy of vertical position). If starting from rest, the mechanical energy of the skier is entirely in the form of potential energy. As the skier begins the descent down the hill, potential energy is lost and kinetic energy (i.e., energy of motion) is gained. As the skier loses height (and thus loses potential energy), she gains speed (and thus gains kinetic energy). Once the skier reaches the bottom of the hill, her height reaches a value of 0 meters, indicating a total depletion of her potential energy. At this point, her speed and kinetic energy have reached a maximum. This energy state is maintained until the skier meets a section of unpacked snow and skids to a stop under the force of friction. The friction force, sometimes known as a dissipative force, does work upon the skier in order to decrease her total mechanical energy. Thus, as the force of friction acts over an increasing distance, the quantity of work increases and the mechanical energy of the skier is gradually dissipated. Ultimately, the skier runs out of energy and comes to a rest position. Work done by an external force (friction) has served to change the total mechanical energy of the skier.
This intricate relationship between work and mechanical energy is depicted in the animation below.
Along the inclined section of the run, the total mechanical energy of the skier is conserved provided that:
-
there is a negligible amount of dissipative forces (such as air resistance and surface friction), and
-
the skier does not utilize her poles to do work and thus contribute to her total amount of mechanical energy
Provided that these two requirements are met, there would be no external forces doing work upon the skier during the descent down the hill. The force of gravity and the normal forces would be the only active forces. While the normal force is an external force, it does not do work upon the skier since it acts at a right angle to the skier's displacement. In such situations where the angle between force and displacement is 90-degrees, the force does not do work upon the skier. Consequently, the force of gravity is the only force doing work on the skier and therefore the total mechanical energy of the skier is conserved. Potential energy is transformed into kinetic energy; and the potential energy lost equals the kinetic energy which is gained. Overall, the sum of the kinetic and potential energy remains a constant value.
The numerical values and accompanying bar chart in the animation above depicts these principles. During the descent down the hill, the height of the total mechanical energy (TME) bar remains a constant quantity, indicating the conservation of total mechanical energy. Furthermore, as the height of the potential energy (PE) bar decreases, the height of the kinetic energy (KE) bar increases.
Near the end of the run, the skier encounters the force of friction. This force acts in the direction opposite the displacement of the skier. The angle between the force and the displacement is 180 degrees. Using the equation for work (F*d*cosine 180 degrees), the amount of work can be calculated. The value calculated from the above equation is a negative number, indicating that the work done serves to remove energy from the object. This is why friction is sometimes referred to as a dissipative force. The amount of work which is done is equal to the loss of mechanical energy. The bar chart in the animation above depicts a work (W) bar with a negative height. As this bar becomes more negative, the height of the total mechanical energy (TME) bar becomes smaller. By the end of the animation, the work bar has reached a height of -8 units and the total mechanical energy bar has change its height from +8 units to 0 units. Thus, the change in height of the total mechanical energy bar (-8 units) equals the height of the work bar (-8 units).
For more information on physical descriptions of motion, visit The Physics Classroom Tutorial. Detailed information is available there on the following topics:
Potential Energy
Kinetic Energy
Mechanical Energy
Internal vs. External Forces
Work
Work-Energy Theorem
Work-Energy Bar Charts