Vector Direction
A vector is a quantity which has both magnitude and direction. Examples of vectors include displacement, velocity, acceleration, and force. To fully describe one of these vector quantities, it is necessary to tell both the magnitude and the direction. For instance, if the velocity of an object were said to be 25 m/s, then the description of the object's velocity is incomplete; the object could be moving 25 m/s south, or 25 m/s north or 25 m/s southeast. To fully describe the object's velocity, both magnitude (25 m/s) and direction (e.g., south) must be stated.
In order for such descriptions of vector quantities to be useful, it is important that everyone agree upon how the direction of an object is described. Most of us are accustomed to the idea that up on a map refers to the northward direction and right on a map refers to the eastward direction. This is a mere convention which mapmakers have used for years and upon which we all can agree. But what is the direction of a vector quantity which is not due north or due east but somewhere in between north and east? For such cases as this, it is important that there be some convention for describing the direction of such a vector. The convention upon which we can all agree is sometimes referred to as the CCW convention - counterclockwise convention. Using this convention, we can describe the direction of any vector in terms of its counterclockwise angle of rotation from due east. The direction north would be at 90 degrees since a vector pointing east would have to be rotated 90 degrees in the counterclockwise direction in order to point north. The direction of west would be at 180 degrees since a vector pointing west would have to be rotated 180 degrees in the counterclockwise direction in order to point west. Further illustrations of the use of this convention are depicted by the animation below.
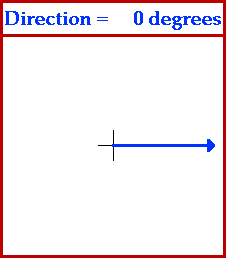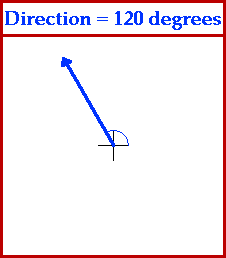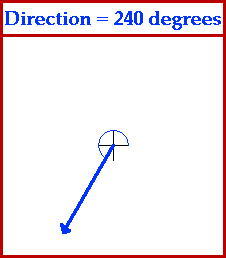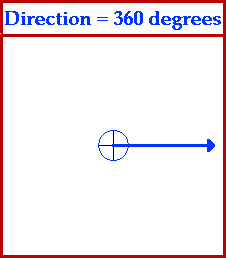
For more information on physical descriptions of motion, visit The Physics Classroom Tutorial. Detailed information is available there on the following topics:
Vectors and Direction
Vector Addition
Vector Components