F_grav = m•g = ~800 N

∑F_y = ma_y = (80 kg)•(2.0 m/s/s)

∑F_y = 160 N, down

The F_grav (down) and the F_air (up) must add up to 160 N, down. Thus, F_air must be smaller than F_grav by 160 N.

F_air = 640 N

Since  F_grav = m•g, m can be calculated to be ~70 kg (m=F_grav/g).

Since a_y = 0 m/s/s, F_norm must equal F_grav; so F_norm = 700 N.

∑F_x = m•a_x = (70 kg)•(5.0 m/s/s)

∑F_x = 350 N, left

(Note that the ·F_x direction is always the same as the a_x direction.)

With F_app being the only horizontal force, its value must be 350 N - the same as ·F_x.

   F_grav = m•g = ~800 N

Since there are two forces pulling upwards and since the sign is hanging symmetrically, each force must supply an upwards pull equal to one-half the object's weight. So the vert pull (F_y) in each force is 400 N. The following triangle can be set up:

Using trig, we can write:

sin(30 deg.)=(400 N)/F_tens

Solving for F_tens yields 800 N.

A quick blank is F_grav:  F_grav = m•g = ~80 N

Now resolve the 60-N force into components using trigonometry and the given angle measure:

F_x = 60 N•cos(30 deg) = 52 N

F_y = 60 N•sin(30 deg) = 25 N

Since the acceleration is horizontal, the sum of the vertical forces must equal 0 N. So F_grav = F_y + F_norm.

Therefore F_norm = F_grav - F_y = 55 N.

Knowing F_norm and mu, the F_frict can be determined:

F_frict = mu•F_norm = 0.5*(55 N) = 27.5 N

Now the horizontal forces can be summed:

∑F_x = F_x + F_frict = 52 N, right + 27.5 N, left

∑F_x = 24.5 N, right

Using Newton's second law, ∑F_x = m•a_x

So a_x = (24.5 N)/(8 kg) = 3.1 m/s/s, right (3.06... m/s/s)

The first step in an inclined plane problem is to resolve the weight vector into parallel and perpendicular components:

F_par = m•g•sin(angle) = (420 N)•sin(30 deg) = 210 N

F_perp = m•g•cos(angle) = (420 N)•cos(30 deg) = 364 N

The mass can be found as m = F_grav/g

m = F_grav/g = (420 N)/(10 m/s/s) = ~42 kg

The F_norm acts opposite of and balances the F_perp.

So F_norm = F_perp = 364 N

Knowing F_norm and mu, the F_frict can be determined:

F_frict = mu•F_norm = 0.2*(364 N) = 73 N

Now the forces parallel to the incline can be summed:

∑F_|| = F_|| + F_frict = 210, down to left + 73 N, up to right

∑F_|| = 137 N, down to left

Using Newton's second law, ∑F_|| = m•a_||

So a_|| = (137 N)/(42 kg) = 3.3 m/s/s

Treating the two masses as a single system, it can be concluded that the net force on the 9-kg system is:

∑F_system = m•a_system = (9 kg)•(2.5 m/s/s) = 22.5 N, right

The free-body diagram for the system is:

The F_norm supporting the 9-kg system is ~90 N.

So the F_frict acting upon the system is:

F_frict = mu• F_norm = 0.20*(90 N) = 18 N, left

So if ∑F_system = 22.5 N, right and F_frict = 18 N, left, the rightward F_tens1 must equal 40.5 N.

The F_tens2 force is found inside the system; as such it can not be determined through a system analysis. To determine the F_tens2, one of the individual masses must be isolated and a free-body analysis must be conducted for it.

The 3-kg mass is selected and analyzed:

The F_norm and F_grav balance each other; their value is ~30 N. The F_frict on the 3-kg mass is:

F_frict = mu•F_norm = 0.20*(30 N) = 6 N, left

The net force on the 3-kg object is:

∑F_x = m•a_x = (3 kg)•(2.5 m/s/s) = 7.5 N, right

The horizontal forces must sum up to the net force on the 3-kg object; So

∑F_x = m•a_x = F_tens2 (right) + F_frict (left)

7.5 N, right = F_tens2 + 6 N, left

The F_tens2 must be 13.5 N.

 Like most two-body problems involving pulleys, it is usually easiest to forgo the system analysis and conduct separate free-body analyses on the individual masses. Free-body diagrams, the chosen axes systems, and associated information is shown below.

Analyzing the F_x forces on the 250-g mass yields:

ma_x = F_tens - F_frict

Since F_frict = mu•F_norm and F_norm = 2.5 N

The F_frict is (0.1)*(2.5 N) = 0.25 N.

Substituting into equation 1 yields

(0.250 kg)•a_x = F_tens - 0.25 N

Analyzing the F_y forces on the 50-g mass yields:

ma_y = F_grav - F_tens

Substituting m and F_grav values into equation 3 yeilds:

(0.050 kg)*a_y = (0.500 N) - F_tens

The above equation can be rearranged to:

F_tens = (0.500 N) - (0.050 kg)*a_y

Equation 4 provides an expression for Ftens; this can be substituted into equation 2:

(0.250 kg)•a_x = (0.500 N) - (0.050 kg)*a_y - 0.25 N

Now since both masses accelerate at the same rate, a_x =a_y

and the above equation can be simplified into an equation with 1 unknown - the acceleration (a):

(0.250 kg)•a = (0.500 N) - (0.050 kg)*a - 0.25 N

After a few algebra steps, the acceleration can be found:

(0.0300 kg)•a = 0.25 N

a = 0.833 m/s/s

Now that a has been found, its value can be substituted back into equation 4 in order to solve for F_tens:

F_tens = (0.500 N) - (0.050 kg)*(0.833 m/s/s)

F_tens = 0.458 N

This problem can most easily be solved using separate free-body analyses on the individual masses. Free-body diagrams, the chosen axes systems, and associated information is shown below.

Note that the positive y-axis is chosen as being downards on the 200-g mass since that is the direction of its acceleration. Similarly, it chosen as upwards on the 100-g mass since that is the direction of its acceleration.

For the 200-gram mass, the sum of the vertical forces equals the mass times the acceleration:

 F_grav - F_tens = m•a_y

2.00 N - F_tens = (0.200 kg)•a_y

The same type of analysis can be conducted for the 100-gram mass:

F_tens - F_grav = m•a_y

F_tens - 1.00 N = (0.100 kg)•a_y

Equation 2 can be rearranged to obtain an expression for the tension force:

F_tens = (0.100 kg)•a_y + 1.00 N

This expression for F_tens can be substituted into equation 1 in order to obtain a single equation with acceleration (a_y) as the unknown. The a_y value can be solved for.

2.00 N -[(0.100 kg)•a_y + 1.00 N] = (0.200 kg)•a_y

2.00 N - 1.00 N = (0.200 kg)•a_y + (0.100 kg)•a_y

1.00 N = (0.300 kg)•a_y

a_y = (1.00 N)/(0.300 kg) = 3.33 m/s/s

Now with a_y known, its value can be substituted into equation 3 in order to determine the tension force:

F_tens = (0.100 kg)•a_y + 1.00 N

F_tens = (0.100 kg)•(3.33 m/s/s) + 1.00 N

F_tens = 0.333 N + 1.00 N = 1.33 N

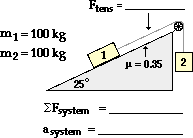
Like #20, this problem can most easily be solved using separate free-body analyses on the individual masses. Free-body diagrams, the chosen axes systems, and associated information is shown below. Note that in chosing the axis system, it has been assumed that object 1 will accelerate up the hill and object 2 will accelerate downwards. If this ends up to be false, then the acceleration values will turn out to be negative values.

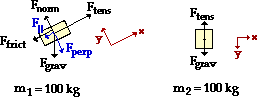
Object 1 is on an inclined plane. The usual circumstances apply; their is no acceleration along what has been designated as the y-axis.

F_norm = F_perp = m•g•cos(theta) = 888.2 N

The parallel component of F_grav is

F_|| = m•g•sin(theta) = (100 kg)•(9.8 m/s²)•sin(25)

F_|| = 414.2 N

The F_frict value can be found from the F_norm value:

F_frict = mu•F_norm = (0.35)•(888.2 N) = 310.9 N

The ∑F_x = m•a_x equation can now be written:

∑F_x = m•a_x

F_tens - F_frict - F_|| = m•a_x

F_tens - 310.9 N - 414.2 N = m•a_x

(Note that the F_frict and F_|| forces are subtracted from F_tens since they are heading in the direction of the negative x-axis.)

The above process can be repeated for object 2. The ∑F_y = m•a_y equation can now be written:

∑F_y = m•a_y

F_grav - F_tens = m•a_y

(980 N) - F_tens = m•a_y

The separate free-body analyses have provided two equations with two unknowns; the task at hand is to use these two equations to solve for F_tens and a.

Equation 2 can be re-written as

(980 N) - m•a_y = F_tens

Since both objects accelerate together at the same rate, the ax for object 1 is equal to the ay value for object 2. The subscripts x and y can be dropped and a can be inserted into each equation.

(980 N) - m•a = F_tens

Equation 3 provides an expression for F_tens in terms of a. This expression is inserted into equation 1 in order to solve for acceleration. The steps are shown below.

(980 N) - m•a - 310.9 N - 414.2 N = m•a

= 2•m•a

254.9 N = 2•(100 kg)•a

1.27 m/s² = a

The value of a can be re-inserted into equation 3 in order to solve for F_tens:

F_tens = (980 N) - m•a =(980 N) - (100 kg)•(1.27 m/s²)

F_tens = 853 N

[ Questions #1-#12 | Questions #13-#21 | Questions #22-#30 ]