Newton's Laws Applications Review
Navigate to:
Review Session Home - Topic Listing
Forces in 2 Dimensions - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-12 || #13-21 || #22-30
Part D: Problem-Solving
22. A 945-kg car traveling rightward at 22.6 m/s slams on the brakes and skids to a stop (with locked wheels). If the coefficient of friction between tires and road is 0.972, determine the distance required to stop. PSYW
|
Answer: 26.8 m
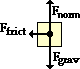 Like most problems, this problem begins with a free-body diagram (as shown at right). Note that there is no rightwards applied force (a common mistake). Note also that the force of friction is the only force responsible for the acceleration (deceleration) of the car. The Ffrict value is the net force. So determining the acceleration involves finding Fgrav (Fgrav=m•g = 945•9.8 = 9261 N), Fnorm (the same as Fgrav= 9261 N), and Ffrict (Ffrict = mu•Fnorm = 0.972 • 9261 N = 9002 N). With the ∑Fx = 9002 N, the acceleration can be calculated (ax = ∑Fx/m = 9002 N/945 kg = 9.53 m/s/s.) This is a leftwards acceleration; ax will be assigned the numerical value of -9.53 m/s/s in the next part of this problem. Like most problems, this problem begins with a free-body diagram (as shown at right). Note that there is no rightwards applied force (a common mistake). Note also that the force of friction is the only force responsible for the acceleration (deceleration) of the car. The Ffrict value is the net force. So determining the acceleration involves finding Fgrav (Fgrav=m•g = 945•9.8 = 9261 N), Fnorm (the same as Fgrav= 9261 N), and Ffrict (Ffrict = mu•Fnorm = 0.972 • 9261 N = 9002 N). With the ∑Fx = 9002 N, the acceleration can be calculated (ax = ∑Fx/m = 9002 N/945 kg = 9.53 m/s/s.) This is a leftwards acceleration; ax will be assigned the numerical value of -9.53 m/s/s in the next part of this problem.
Now in the kinematic part of this problem, the distance must be found using the known information (vf = 0 m/s, vo = 22.6 m/s and a = 9.53 m/s/s). Use the equation:
vf2 = vo2 + 2 a d
(0 m/s)2 = (22.6 m/s)2 + 2•(-9.53 m/s/s)•d
d = [(22.6 m/s)2] / [2•(9.53 m/s/s)] = 26.8 m
|
[ #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 ]
23. A student pulls a 2-kg backpack across the ice (assume frictionless) by pulling at a 30.0 degrees angle to the horizontal. The velocity-time graph for the motion is shown. Perform a careful analysis of the situation and determine the applied force. PSYW
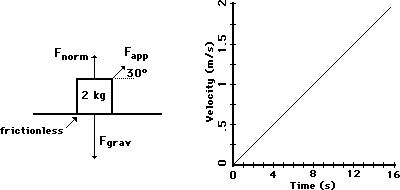
|
Answer: 0.289 N
The acceleration of the object can be found from the slope of the line on the v-t graph. The acceleration is:
a = change in velocity/change in time = (2.0 m/s) / 16 s = 0.125 m/s/s.
The net force is found from m•a; so Fnet = (2 kg)•(0.125 m/s/s) = 0.250 N.
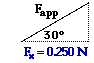 The only force that can contribute to the net force is the applied force. The horizontal component of the applied force must therefore be equal to 0.250 N. A diagram depicting the relationship of the lengths of the side for this 30-60-90 triangle is shown at the right. The cosine function can be utilized to determine the magnitude of the tension force. The only force that can contribute to the net force is the applied force. The horizontal component of the applied force must therefore be equal to 0.250 N. A diagram depicting the relationship of the lengths of the side for this 30-60-90 triangle is shown at the right. The cosine function can be utilized to determine the magnitude of the tension force.
cos(30 deg) = 0.250 N)/Fapp
Solving for Fapp yields 0.289 N.
|
 24. After its most recent delivery, the infamous stork announces the good news. If the sign has a mass of 10.0 kg, then what is the tensional force in each cable?
24. After its most recent delivery, the infamous stork announces the good news. If the sign has a mass of 10.0 kg, then what is the tensional force in each cable?
|
Answer: 56.6 N
If the mass of the sign is 10.0 kg, then the weight of the sign is 98 N (Fgrav = m•g). This downward force of gravity must be balanced by the upward component of the tension. Thus, each cable must pull upwards with 49.0 N of force. 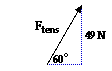 In addition to the upward pull by the cable, there is also a horizontal pull. The tension force is the combined effect of these two componens. To determine the tension, set up a 60-30-90 triangle with a vertical component of 4.09 N as shown at the right. Then, use the sine function to solve for the hypotenuse of the triangle. The work is shown below: In addition to the upward pull by the cable, there is also a horizontal pull. The tension force is the combined effect of these two componens. To determine the tension, set up a 60-30-90 triangle with a vertical component of 4.09 N as shown at the right. Then, use the sine function to solve for the hypotenuse of the triangle. The work is shown below:
sin(60 deg.) = 49.0 N/Ftens
Ftens = (49.0 N)/(sin 60 deg) = 56.6 N
|
25. Splash Mountain at Disney World in Orlando, Florida is one of the steepest water plume rides in the United States. Occupants of the boat fall from a height of 100 feet (3.2 ft = 1 m) down a wet ramp which makes a 45 degree angle with the horizontal. Consider the mass of the boat and its occupants to be 1500 kg. The coefficient of friction between the boat and the ramp is 0.10. Determine the frictional force, the acceleration, the distance traveled along the incline, and the final velocity of the boat at the bottom of the incline. PSYW
|
Answer: All numerical answers are rounded to two significant digits: Ffrict = ~1040 N; a = ~6.2 m/s/s; d = ~44 m; vf = 23 m/s
This is a multi-part inclined plane problem. Like all problems, it should begin with a free-body diagram. If this is 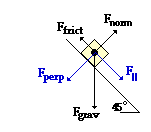 where the difficulty lies for you, then take some time to review inclined planes. See help page. The friction force opposes the motion of the boat. If the + x direction is defined as down and along the incline (as shown at the right) then the net force can be computed by the expression F|| - Ffrict. The parallel component of the weight vector (m•g•sin theta) is 10395 N. The Ffrict force is computed by multiplying the coefficient of friction (0.10) by the normal force (Fnorm). The normal force is balancing Fperp (m•g•cos theta) and is equal to it. So Fnorm = 10395 N and Ffrict = 1039.4 N. The net force (Fnet = F|| - Ffrict ) is 9356 N; and the acceleration is Fnet/m or 6.24 m/s/s. where the difficulty lies for you, then take some time to review inclined planes. See help page. The friction force opposes the motion of the boat. If the + x direction is defined as down and along the incline (as shown at the right) then the net force can be computed by the expression F|| - Ffrict. The parallel component of the weight vector (m•g•sin theta) is 10395 N. The Ffrict force is computed by multiplying the coefficient of friction (0.10) by the normal force (Fnorm). The normal force is balancing Fperp (m•g•cos theta) and is equal to it. So Fnorm = 10395 N and Ffrict = 1039.4 N. The net force (Fnet = F|| - Ffrict ) is 9356 N; and the acceleration is Fnet/m or 6.24 m/s/s.
Once the Newton's laws analysis has been completed and the acceleration determined, the kinematics portion of the problem can be tackled. First, determine the distance along the incline from the height of the hill and the angle of incline. The height of 100 ft is equivalent to 31.25 m; the distance along the incline is 44.19 m [found from (31.25 m)/sin (45)]. The final velocity is found using the acceleration, distance and a kinematic equation:
vf2 = vo2 + 2•a•d
vf2 = (0 m/s)2 + 2•(6.24 m/s/s)•(31.25 m) = 551.28 m2/s2
vf = 23 m/s
|
26. At last year's Homecoming Pep Rally, Trudy U. Skool (attempting to generate a little excitement) slid down a 42.0 degree incline from the sports dome to the courtyard below. The coefficient of friction between Trudy's jeans and the incline was 0.650. Determine Trudy's acceleration along the incline. Begin with a free-body diagram. PSYW
|
Answer: 1.82 m/s/s
This is nearly an identical force analysis as the last problem except the mass is not known. When the mass is not known, the problem-solving strategy involves inserting m into the equation as an unknown variable and proceding with the solution. It is likely that in a subsequent step of the problem that the m will cancel and the accceleration can be determined without knowing m.
The net force is found by the expression F|| - Ffrict. The parallel component of the weight vector is m•g•sin(theta). The Ffrict force is computed by multiplying the coefficient of friction (mu) by the normal force (Fnorm). The normal force is balancing Fperp and is equal to m•g•cos(theta). So Fnorm = m•g•cos(theta) and Ffrict = µ•m•g•cos(theta). The net force is m•g•sin(theta) - µ•m•g•cos(theta). The acceleration is Fnet/m or [m•g•sin(theta) - µ•m•g•cos(theta)]/m. Note that there is an m in both terms in the numerator and a m in the denominator. The masses cancel and the equation reduces to
a = [g•sin(theta) - µ•g•cos(theta)]
By substitution of the given values into the equation, it can be shown that a = 1.82 m/s/s.
|
[ #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 ]
27. Baldwin Young is conducting his famous toupee experiments. He tips his head at a given angle and determines the coefficient of static and kinetic friction between a toupee (which is probably his own) and his scalp. At an angle of just barely 17.5 degrees, the toupee begins to accelerate from rest. Then Baldwin lowers the angle to 13.8 degrees to observe that the toupee moves with a constant speed. Use this information to determine the coefficients of both static and kinetic friction. Begin with a free-body diagram. PSYW
|
Answer: µstatic = 0.315; µkinetic = 0.246
A free-body diagram and a force analysis will yield the equation
Ffrict = F||
for both the static and the kinetic situation. That is, when the object is at rest or moving down the incline at constant speed, the force down and parallel to the incline is balanced by the force which is up and parallel to the incline. The expressions for Ffrict and F|| can be substituted into this equation to yield
µ•Fnorm = m•g•sin(theta)
Knowing that Fnorm is equal in magnitude to Fperp, the expression for Fperp can be substituted into the equation for Fnorm. The new equation becomes
µ•m•g•cos(theta) = m•g•sin(theta)
The angles for both the static and the kinetic case are known and mu (coefficient of friction) is the unknown. So the equation can be re-arranged to
µ = m•g•sin(theta)/m•g•cos(theta)
The mass (m) and the acceleration of gravity (g) cancel from both the numerator and the denominator leaving sin(theta)/cos(theta) on the right side. This can be simplified again to
 µ = tan(theta) µ = tan(theta)
Equation 1 can be used to find the coefficient of friction for both the static and kinetic situation. The answers are as follows:
µstatic = tan(17.5 deg.) = 0.315
µkinetic = tan(13.8 deg.) = 0.246
|
[ #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 ]
28. Consider the two-body system at the right. There is a 0.250-kg object accelerating across a rough surface. The sliding object is attached by a string to a 0.100 kg object which is suspended over a pulley. The coefficient of kinetic friction is 0.183. Calculate the acceleration of the block and the tension in the string. PSYW

|
Answer: a = 1.52 m/s/s ; Ftens = 0.83 N
The solution to this problem begins by drawing a free-body diagram for each object. Note that the + x-axis for the 0.25-kg object is drawn in the direction that the object accelerates; and the + y-axis for the 0.10-kg object is drawn in the direction which it accelerates.
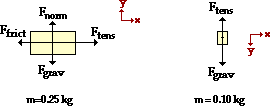
Note that while friction acts upon the 0.25-kg object, it does not act upon the 0.10-kg object (since it is not being dragged across the surface). Newton's second law of motion (·F = m•a) can be applied to the motion of the 0.25-kg mass:
∑Fx = m•ax
Ftens - Ffrict = m•ax
The expressioin for Ffrict can be substituted into the equation.
 Ftens - µ•Fnorm = m•ax Ftens - µ•Fnorm = m•ax
Since the vertical forces on the 0.250-kg object balance each other, it is known that Fgrav = Fnorm; so Fnorm = m•g = (0.250 kg)•(9.8 m/s/s) = 2.45 N. Since µ = 0.183, µ•Fnorm = 0.448 N. Equation 1 can now be re-written as
 Ftens - 0.448 N = (0.250 kg)•ax Ftens - 0.448 N = (0.250 kg)•ax
Newton's second law of motion (∑F = m•a) can be applied to the motion of the 0.10o-kg mass:
∑Fy = m•ay
Fgrav - Ftens = m•ay
The expression for Fgrav (m•g) can be substituted into the equation.
m•g - Ftens = m•ay
(0.100 kg)•(9.8 m/s/s) - Ftens = m•ay
0.98 N - Ftens = m•ay
The mass of the 0.100-kg object can be substituted into the equation to yield equation 3.
 0.98 N - Ftens = (0.100 kg)•ay 0.98 N - Ftens = (0.100 kg)•ay
Equations 2 and 3 each include an acceleration term - ax and ay. These acceleration values are the same since the system accelerates together; thus, ax = ay = a. An inspection of these two equations show that there are now two equations and two unknowns - Ftens and a. These unknown values can be solved for in the customary manner.
First, equation 3 is rearranged to create an expression for Ftens:
 0.98 N - (0.100 kg)•a = Ftens 0.98 N - (0.100 kg)•a = Ftens
This expression for Ftens is now substituted into equation 2.
 Ftens - 0.448 N = (0.250 kg)•a Ftens - 0.448 N = (0.250 kg)•a
0.980 N - (0.100 kg)•a - 0.448 N = (0.250 kg)•a
This equation can now be solved for acceleration (a) as shown in the following steps.
0.980 N - 0.448 N = (0.250 kg)•a + (0.100 kg)•a
0.532 N = (0.305 kg)•a
a = 1.52 m/s/s
Now that a is known, its value can be substituted into equation 4 in order to solve for Ftens.
0.980 N - (0.100 kg)•a = Ftens
0.980 N - (0.10 kg)•(1.52 m/s/s) = Ftens
0.980 N - 0. 152 N = Ftens
0.830 N = Ftens
|
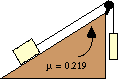 29. Consider the two-body system at the right. A 22.7-N block is placed upon an inclined plane which is inclined at a 17.2 degree angle. The block is attached by a string to a 34.5-N block which is suspended over a pulley. The coefficient of friction is 0.219. Determine the acceleration of the block and the tension in the string. PSYW
29. Consider the two-body system at the right. A 22.7-N block is placed upon an inclined plane which is inclined at a 17.2 degree angle. The block is attached by a string to a 34.5-N block which is suspended over a pulley. The coefficient of friction is 0.219. Determine the acceleration of the block and the tension in the string. PSYW
|
Answer: a = 3.95 m/s/s; Ftens = 20.6 N
Like #21 and #28, this problem can most easily be solved using separate free-body analyses on the individual masses. Free-body diagrams, the chosen axes systems, and associated information is shown below. Note that in chosing the axis system, it has been assumed that object 1 will accelerate up the hill and object 2 will accelerate downwards on the back side of the hill. If this ends up to be false, then the acceleration values will turn out to be negative values.
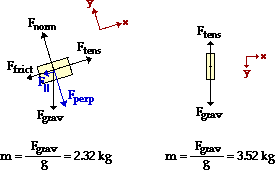
The 22.7-N object is on an inclined plane. The usual circumstances apply; there is no acceleration along what has been designated as the y-axis.
Fnorm = Fperp = m•g•cos(theta) = 21.7 N
The parallel component of Fgrav is
F|| = m•g•sin(theta) = (22.7 N)•sin(17.2)
F|| = 6.71 N
The Ffrict value can be found from the Fnorm value:
Ffrict = µ•Fnorm = (0.219)•(21.7 N) = 4.75 N
The ∑Fx = m•ax equation can now be written:
∑Fx = m•ax
Ftens - Ffrict - F|| = m•ax
 Ftens - 4.75 N - 6.71 N = (2.32 kg)•ax Ftens - 4.75 N - 6.71 N = (2.32 kg)•ax
(Note that the Ffrict and F|| forces are subtracted from Ftens since they are heading in the direction of the negative x-axis.)
The above process can be repeated for the 34.5-N object. The ∑Fy = m•ay equation can now be written:
∑Fy = m•ay
Fgrav - Ftens = m•ay
 (34.5 N) - Ftens = (3.52 kg)•ay (34.5 N) - Ftens = (3.52 kg)•ay
The separate free-body analyses have provided two equations with two unknowns; the task at hand is to use these two equations to solve for Ftens and a.
Equation 2 can be re-written as
(34.5 N) - (3.52 kg)•ay = Ftens
Since both objects accelerate together at the same rate, the ax for the 22.7-N object is equal to the ay value for the 34.5-N object. The subscripts x and y can be dropped and a can be inserted into each equation.
 (34.5 N) - (3.52 kg) •a = Ftens (34.5 N) - (3.52 kg) •a = Ftens
Equation 3 provides an expression for Ftens in terms of a. This expression is inserted into equation 1 in order to solve for acceleration. The steps are shown below.
Ftens - 4.75 N - 6.71 N = (2.32 kg)•a
(34.5 N) - (3.52 kg) •a - 4.75 N - 6.71 N = (2.32 kg)•a
23.0 N = (5.84 kg)•a
3.95 m/s2 = a
The value of a can be re-inserted into equation 3 in order to solve for Ftens:
Ftens = (34.5 N) - (3.52 kg) • (3.95 m/s2)
Ftens = 20.6 N
|
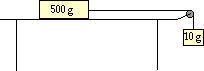
30. A 10.0-gram mass is tied to a string. The string is attached to a 500.0-gram mass and stretched over a pulley, leaving the 10.0-gram mass suspended above the floor. Determine the time it will take the 10.0-gram mass to fall a distance of 1.50 meters if starting from rest. (No friction)
|
Answer: t = 3.95 s
This problem involves a blending of Newton's laws and kinematics. Newton's laws will have to be used to determine the acceleration; then kinematics will have to be used to determine the time to fall 1.50 m from rest. The solution to this problem begins by drawing a free-body diagram for each object. Note that the + x-axis for the 500.0-gram object is drawn in the direction that the object accelerates; and the + y-axis for the 10.0-gram object is drawn in the direction which it accelerates.
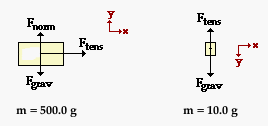
Note that while friction acts upon the 500.0-gram object, it does not act upon the 10.0-gram object (since it is not being dragged across the surface). Newton's second law of motion (∑F = m•a) can be applied to the motion of the 0.5000-kg mass:
∑Fx = m•ax
Ftens = m•ax
Ftens = (0.5000 kg)•a x x
Newton's second law of motion (∑F = m•a) can also be applied to the motion of the 0.0100-kg hanging mass:
∑Fy = m•ay
Fgrav - Ftens = m•ay
The expression for Fgrav (m•g) can be substituted into the equation.
m•g - Ftens = m•ay
(0.0100 kg)•(9.8 m/s/s) - Ftens = m•ay
0.098 N - Ftens = m•ay
The mass of the 0.0100-kg object can be substituted into the equation to yield equation 2.
0.098 N - Ftens = (0.0100 kg)•a y y
Equations 1 and 2 include an acceleration term - ax and ay. These acceleration values are the same since the system accelerates together; thus, ax = ay = a. An inspection of these two equations show that there are now two equations and two unknowns - Ftens and a. These unknown values can be solved for in the customary manner. First, equation 2 is rearranged so as to express Ftens in terms of a. This yields equation 3.
 Ftens = 0.098 N - (0.0100 kg)•ay Ftens = 0.098 N - (0.0100 kg)•ay
Equations 1 and 3 both express Ftens in terms of a. The right side of each equation is equal to Ftens ; so these two right sides can be set equal to each other to yield the following equation.
(0.5000 kg)•ax = 0.098 N - (0.0100 kg)•ay
Since ax is equal to ay, the equation can be re-written as
(0.5000 kg)•a = 0.098 N - (0.0100 kg)•a
where a is the horizontal and the vertical acceleration of the 500.0-gram and 10.0-gram masses. Now the above equation can be manipulated in order to solve for the value of a.
(0.5000 kg)•a + (0.0100 kg)•a = 0.098 N
(0.510 kg)•a = 0.098 N
a = (0.098 N) / (0.510 kg)
a = 0.1922 m/s/s
Now that an acceleration has been determined, the time can be calculated using a kinematic equation. The three known kinematic quantities are:
vi = 0 m/s
a = 0.1922 m/s/s
d = 1.50 m
The following kinematic equation can be used to solve for time (t). The substitutions and algebra are shown.
d = vi•t + 0.5 •a• t2
1.50 m = (0 m/s) • t + 0.5•(.1922 m/s/s)•t2
1.50 m = (0.0961 m/s/s)•t2
t2 = (1.50 m) / (0.0961 m/s/s)
t2 = 15.6087 s2
t = SQRT(15.6087 s2)
t = 3.95 s
|
Navigate to:
Review Session Home - Topic Listing
Forces in 2 Dimensions - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-12 || #13-21 || #22-30
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Forces in Two Dimensions
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 2 of the series includes Forces in Two Dimensions.
Visit: MOP the App Home || MOP the App - Part 2