The Physics Classroom

» The Physics Classroom » Review Session » Newton's Laws of Motion

Newton's Laws of Motion Review

Navigate to Answers for:

Questions #1-7
Questions #8-#36
Questions #37-#46
Questions #47-#60


[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

Part F: Problem-Solving

For the following problems, draw free-body diagrams and solve for the requested unknown. Use g = 9.8 m/s/s.

The following links may lead to useful information for questions #47-60:

Useful Web Links

Free-Body Diagrams || Finding Acceleration || Finding Individual Forces || Kinematic Equations and Problem-Solving


47. A 0.250-kg ball is thrown upwards with an initial velocity of 12.0 m/s at an angle of 30.0 degrees. Determine the acceleration of the ball when it has reached the peak of its trajectory. Assume negligible air resistance. PSYW

Answer: 9.8 m/s/s, down

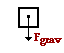There is only one force upon the ball - the force of gravity. (Air resistance is negligible; the ball is not on a surface, so there is no friction or normal force; the applied force which projects it into motion does not act upon the ball during its trajectory; there are no springs, strings, wires, or cables attached so there is neither a tension force nor a spring force.) The force of gravity acts downward with a magnitude of m•g = (0.250 kg) •(9.8 m/s/s) = 2.45 N. The net force is 2.45 N; when divided by mass, the acceleration can be found.

 a = Fnet / m = (2.45 N, down) / (0.250 kg) = 9.8 m/s/s, down

[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

48. A 72-kg skydiver is falling from 10000 feet. At an instant during the fall, the skydiver encounters an air resistance force of 540 Newtons. Determine the acceleration of the skydiver at this instant. PSYW

Answer: 2.3 m/s/s, down

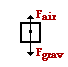There are two forces acting upon the skydiver - gravity (down) and air resistance (up).  The force of gravity has a magnitude of m•g = (72 kg) •(9.8 m/s/s) = 706 N. The sum of the vertical forces is

∑Fy = 540 N, up + 706 N, down = 166 N, down

The acceleration of the skydiver can be computed using the equation ∑Fy = m•ay.

ay = (166 N, down) / (72 kg) = 2.3 m/s/s, down


[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ]  

49. A 72-kg skydiver is falling from 10 000 feet. After reaching terminal velocity, the skydiver opens his parachute. Shortly thereafter, there is an an instant in time in which the skydiver encounters an air resistance force of 1180 Newtons. Determine the acceleration of the skydiver at this instant. PSYW

Answer: 6.6 m/s/s, up

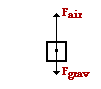There are two forces acting upon the skydiver - gravity (down) and air resistance (up). The force of gravity has a magnitude of m•g = (72 kg) •(9.8 m/s/s) = 706 N. The sum of the vertical forces is

∑Fy = 1180 N, up + 706 N, down = 474 N, up

The acceleration of the skydiver can be computed using the equation ∑Fy = m•ay.

ay = (474 N, up) / (72 kg) = 6.6 m/s/s, up

[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

50. A 5.20-N force is applied to a 1.05-kg object to accelerate it rightwards across a friction-free surface. Determine the acceleration of the object. (Neglect air resistance.) PSYW

Answer: 4.95 m/s/s, right

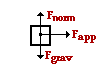Upon neglecting air resistance, there are three forces acting upon the object. The up and down force balance each other and the acceleration is caused by the applied force. The net force is 5.20 N, right (equal to the only rightward force - the applied force). So the acceleration of the object can be computed using Newton's second law.

 a = Fnet / m = (5.20 N, right) / (1.05 kg) = 4.95 m/s/s, right


[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

51. A 5.20-N force is applied to a 1.05-kg object to accelerate it rightwards. The object encounters 3.29-N of friction. Determine the acceleration of the object. (Neglect air resistance.) PSYW

Answer: 1.82 m/s/s, right

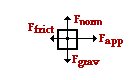Upon neglecting air resistance, there are four forces acting upon the object. The up and down forces balance each other. The acceleration is rightward since the rightward applied force is greater than the leftward friction force. The horizontal forces can be summed as vectors in order to determine the net force.

Fnet = ∑Fx = 5.20 N, right - 3.29 N, left = 1.91 N, right

The acceleration of the object can be computed using Newton's second law.

 ax = ∑Fx / m = (1.91 N, down) / (1.05 kg) = 1.82 m/s/s, right

[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

52. Determine the applied force required to accelerate a 3.25-kg object rightward with a constant acceleration of 1.20 m/s/s if the force of friction opposing the motion is 18.2 N. (Neglect air resistance.) PSYW

Answer: 22.1 N

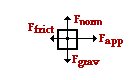There are four forces acting upon the object as shown in the free-body diagram at the right. The two vertical forces must balance since there is no vertical acceleration. Since the mass and the acceleration are known, the net force can be computed:

Fnet = m•a = (3.25 kg, right) • (1.20 m/s/s) = 3.90 N, right

Since the acceleration is to the right, the net force is directed to the right. Thus, the rightward force (applied force) must exceed the leftward force (friction force) by an amount equal to the 3.9 N. So the applied force can be computed.

Fapp = Ffrict + Fnet = 18.2 N + 3.90 N = 22.1 N

[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

53. A 921-kg sports car is moving rightward with a speed of 29.0 m/s. The driver suddenly slams on the brakes and the car skids to a stop over the course of 3.20 seconds with the wheels locked. Determine the average resistive force acting upon the car. PSYW

Answer: 8350 N

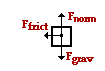There are three (perhaps four) forces acting upon this car. There is the upward force (normal force) and the downward force (gravity); these two forces balance each other since there is no vertical acceleration. The resistive force is likely a combination of friction and air resistance. These forces act leftward upon a rightward skidding car. In the free-body diagram, these two forces are represented by the Ffrict arrow.

The acceleration is not given but can be calculated from the kinematic information that is given:

vi = 29.0 m/s, vf = 0 m/s, and t = 3.20 s

The acceleration of the object is the velocity change per time:

a = Delta v / t = (0 m/s - 29.0 m/s) / (3.20 s) = -9.67 m/s/s or 9.67 m/s/s, left.

This acceleration can be used to determine the net force:

Fnet = m•a = (921 kg) • (9.67 m/s/s, left) = 8350 N, left

The friction forces (surface and air) provide this net force and are equal in magnitude to this net force.

[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

54. A 0.250-kg rightward moving air track glider decreases its speed from 0.872 m/s to 0.798 m/s over the length of a 1.71-m long air track. Determine the average resistive force acting upon the air track glider. PSYW

Answer: 0.00903 N

This problem is similar to the previous problem. There are three (and perhaps four) forces acting upon the glider. The up force could be considered to be a normal force or an air resistance force (from the air blowing through the air track holes). Like the previous problem, the acceleration is not given but it can be calculated from the kinematic information:

vi = 0.872 m/s, vf = 0.798 m/s, and d = 1.71 m

Using a kinematic equation, the values for initial and final velocity and displacement can be substituted; the algebraic steps are shown below.

vf2 = vi2 + 2•a•d

(0.872 m/s)2 = (0.798 m/s)2 + 2•a•(1.71 m)

(0.872 m/s)2 - (0.798 m/s)2 = 2•a•(1.71 m)

0.124 m2/s2 = (3.42 m)•a

0.0361 m/s/s = a

This acceleration can be used to determine the net force:

Fnet = m•a = (0.250 kg) • (0.0361 m/s/s, left) = 0.00903 N, left

The friction forces (surface and air) provide this net force and are equal in magnitude to this net force.

[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

55. A 1250-kg small aircraft decelerates along the runway from 36.6 m/s to 6.8 m/s in 5.1 seconds. Determine the average resistive force acting upon the plane. (Assume that its engine/propeller makes no contributes to its forward motion). PSYW

Answer: 7.30 x 103 N

This problem is similar to the two previous problems in many respects: the free-body diagram is identical or similar and the acceleration is not given but determinable from the kinematic information.

vi = 36.6 m/s, vf = 6.80 m/s, and t = 5.10 s

The acceleration of the object is the velocity change per time:

a = Delta v / t = (6.80 m/s - 36.6 m/s) / (5.10 s) = -5.84 m/s/s or 5.84 m/s/s, left.

This acceleration can be used to determine the net force:

Fnet = m•a = (1250 kg) • (5.84 m/s/s, left) = 7.30 x 103 N, left

The friction forces (surface and air) provide this net force and are equal in magnitude to this net force.

[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

56. A tow truck exerts a 18300-N force upon a 1210-kg car to drag it out of a mud puddle onto the shoulder of a road. A 17900 N force opposes the car's motion. The plane of motion of the car is horizontal. Determine the time required to drag the car a distance of 6.90 meters from its rest position. PSYW

Answer: 6.46 s

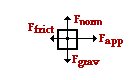Upon neglecting air resistance, there are four forces acting upon the object. The up and down forces balance each other. The acceleration is rightward (or in the direction of the applied force) since the rightward applied force is greater than the leftward friction force. The horizontal forces can be summed as vectors in order to determine the net force.

Fnet = ·Fx = 18300 N, right - 17900 N, left = 400 N, right

The acceleration of the object can be computed using Newton's second law.

 ax = ·Fx / m = (400 N, down) / (1210 kg) = 0.3306 m/s/s, right

This acceleration value can be combined with other known kinematic information (vi = 0 m/s, d = 6.90 m) to determine the time required to drag the car a distance of 6.9 m. The following kinematic equation is used; substitution and algebra steps are shown.

d = vi • t + 0.5 •a • t2

d = vi • t + 0.5 •a • t2

6.90 m = 0.5 • (0.3306 m/s/s) • t2

6.90 m / (0.5 • 0.3306 m/s/s ) = t2

41.4 = t2

6.46 s = t

 
[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

57. A 4.44-kg bucket suspended by a rope is accelerated upwards from an initial rest position. If the tension in the rope is a constant value of 83.1 Newtons, then determine the speed (in m/s) of the bucket after 1.59 seconds. PSYW

Answer: 14.2 m/s

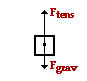There are two forces acting upon the bucket - the force of gravity (up) and the tension force (down). The magnitude of the force of gravity is found from m•g; its value is 43.5 N. These two forces can be summed as vectors to determine the net force.

Fnet = ·Fy = 83.1 N, up + 43.5 N, down = 39.6 N, up

The acceleration can be calculated using Newton's second law of motion.

a = Fnet / m = (39.6 N, up) / (4.44 kg) = 8.92 m/s/s, up

The acceleration value can be used with other kinematic information (vi = 0 m/s, t = 1.59 s) to calculate the final speed of the bucket. The kinematic equation, substitution and algebra steps are shown.

vf = vi + a•t

vf = 0 m/s + (8.92 m/s/s)•(1.59 s)

vf = 14.2 m/s

[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

58. A 22.6-N horizontal force is applied to a 0.0710-kg hockey puck to accelerate it across the ice from an initial rest position. Ignore friction and determine the final speed (in m/s) of the puck after being pushed for a time of .0721 seconds.

Answer: 23.0 m/s

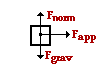Upon neglecting air resistance, there are three forces acting upon the object. The up and down force balance each other and the acceleration is caused by the applied force. The net force is 22.6 N, right (equal to the only rightward force - the applied force). So the acceleration of the object can be computed using Newton's second law.

 a = Fnet / m = (22.6 N, right) / (0.0710 kg) = 318 m/s/s, right

The acceleration value can be used with other kinematic information (vi = 0 m/s, t = 0.0721 s) to calculate the final speed of the puck. The kinematic equation, substitution and algebra steps are shown.

vf = vi + a•t

vf = 0 m/s + (318 m/s/s)•(0.0721 s)

vf = 23.0 m/s


[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

59. A train has a mass of 6.32x104 kg and is moving with a speed of 94.3 km/hr. The engineer applies the brakes which results in a net backward force of 2.43x105 Newtons on the train. The brakes are held for 3.40 seconds. How far (in meters) does the train travel during this time?

Answer: 66.8 m

There are three (perhaps four) forces acting upon this train. There is the upward force (normal force) and the downward force (gravity); these two forces balance each other since there is no vertical acceleration. The resistive force is likely a combination of friction and air resistance. These forces act leftward upon a rightward skidding train. In the free-body diagram, these two forces are represented by the Ffrict arrow. The value of this resistive force is given as 2.43x105 N. This is the net force since there are no other horizontal forces; it is the force which causes the acceleration of the train. The acceleration value can be determined using Newton's second law of motion.

a = Fnet / m = (2.43x105 N) / (6.32x104 kg) = 3.84 m/s/s, left

This acceleration value can be combined with other kinematic variables (vi = 94.3 km/hr = 26.2 m/s; t = 3.4 s) in order to determine the distance the train travels in 3.4 seconds.

d = vi • t + 0.5 •a • t2

d = (26.2 m/s) • (3.40 s) + 0.5•(-3.84 m/s/s) • (3.40 s)2

d = 89.1 m - 22.2 m

d = 66.8 m



[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

60. A shopper in a supermarket pushes a loaded cart with a horizontal force of 16.5 Newtons. If the cart has a mass of 33.8 kg, how far (in meters) will it move in 1.31 seconds, starting from rest? (Neglect frictional effects.)


Answer: 0.419 m

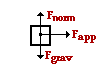Upon neglecting air resistance, there are three forces acting upon the object. The up and down force balance each other and the acceleration is caused by the applied force. The net force is 22.6 N, right (equal to the only rightward force - the applied force). So the acceleration of the object can be computed using Newton's second law.

 a = Fnet / m = (16.5 N, right) / (33.8 kg) = 0.488 m/s/s, right

The acceleration value can be used with other kinematic information (vi = 0 m/s, t = 1.31 s) to calculate the final speed of the cart. The kinematic equation, substitution and algebra steps are shown.

d = vi • t + 0.5 •a • t2

d = vi • t + + 0.5 • (0.488 m/s/s)•(1.31 s) 2

d = 0.419 m


[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 


The following links may lead to useful information for Questions #47-#60:

Useful Web Links

Free-Body Diagrams || Finding Acceleration || Finding Individual Forces || Kinematic Equations and Problem-Solving
 

[  #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 ] 

 

Navigate to Answers for:

Questions #1-7
Questions #8-#36
Questions #37-#46
Questions #47-#60