Refraction and Lenses Review
Navigate to:
Review Session Home - Topic Listing
Refraction and Lenses - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#20 || #21-#34 || #35-#46
Part C: Diagramming and Analysis
|
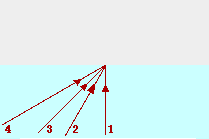
35. The diagram below shows four incident rays traveling through water (n = 1.33) and approaching the boundary with air (n=1.00). For each incident ray, draw the corresponding reflected ray; then calculate the angle of refraction and draw the corresponding refracted ray. Label or color code your reflected and refracted rays to distinguish them from each other and to match them to the incident ray.
|
Ray
|
Angle of
incidence
|
Angle of
reflection
|
Angle of
refraction
|
|
1
|
0.0 deg.
|
0.0 deg.
|
0.0 deg.
|
|
2
|
30.0 deg.
|
30.0 deg.
|
41.7 deg.
|
|
3
|
45.0 deg.
|
45.0 deg.
|
70.1 deg
|
|
4
|
60.0 deg.
|
60.0 deg.
|
None
|
 |
|
|
|
|
Answer: See diagram above
The angle of reflection equals the angle of incidence; this is simply the law of reflection. Each angle is measured relative to the normal.
The angle of refraction is determined using Snell's law. For the 30.0-degree angle, the work would be:
nwater * sin(Angle in water) = nair * sin(Angle in air)
1.33 * sin(30.0 deg) = 1.00 * sin(Angle in air)
0.665 = sin(Angle in air)
invsin(0.665) = Angle in air
41.7 deg = Angle in air
The same calculations are done for the other angles to determine the angle of refraction. In the case of the 60.0 degree angle, the mathematics breaks down and the equation cannot be solved for an angle of refraction. This is because refraction does not occur at the water-air boundaries when light is incident in water at angles of incidence greater than the critical angle (approx. 48 degrees).
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
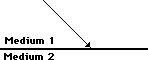
36. In the diagrams below, construct refracted rays to indicate the direction which the light rays bend upon crossing the boundary.
If light travels faster in medium 1 than in medium 2, then upon entering medium 2, the light will bend towards from the normal.
|
If the index of refraction of medium 1 is greater than medium 2, then upon entering medium 2, the light will bend away from the normal.
|
|

|
|
Answer: See diagram above.
On the left, light is moving from a medium in which it travels fast to one in which it travels slow. In such a case, light refracts towards the normal. (Remember fast to slow bends towards as in "FST" or "Freaky Science Teachers".) The refracted ray should be drawn closer to the normal than the incident ray is.
On the right, light is moving from a medium which is more dense or slower to a medium which is less dense or faster. In such a case, light refracts away from the normal. (Remember slow to fast bends away - "SFA" or "Suzie Farts Alot" or "Sammy Farts Alot" or "Somebody Farts Alot".) The refracted ray should be draw farther away from the normal than the incident ray is.
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
37. Use Snell's law, a protractor and a straightedge to trace the path of light through the following objects.
|
Answer: See diagrams above.
Part A
The original incident angle can be measured by drawing a normal at the surface and measuring the angle between the incident ray and the normal; or it can be determined geometrically using the alternating angles theorem. Either way, the incident angle is 45 degrees. The refracted angle can be determined using Snell's law (1.00*sin(45.0 deg) = 1.40*sin(theta)); the angle of refraction is 30.3 degrees. The refracted ray at the entry surface can be drawn and traced through the prism to the opposite face of the triangle.
Once reaching the top face of the triangle, the light ray undergoes total internal reflection (TIR). This would have to be first checked by comparing the incident angle to the critical angle. The critical angle for this boundary is 45.6 degrees (invsin(1/1.40)). The incident angle can be measured by drawing the normal or determined geometrically. In either case, the angle of incidence at the top surface is 75.3 degrees. Since this angle is greater than the critical angle, TIR occurs. The ray reflects according to the law of reflection and continues through the prism to the opposite face.
At the right face, the angle of incidence is 30.3 degrees. This can be determined geometrically or by drawing a normal and measuring the angle between the normal and the incident ray. Finally, the angle of refraction of light at this back surface can be computed using Snell's law; the angle is 45 degrees (invsin(1.40)sin(30.3 deg))). The exiting light ray can be drawn at an angle of 45.0 degrees from the normal.
Part B
At the entry surface, the light ray approaches with an incident angle of 0 degrees. At this angle, no refraction occurs and the light ray continues across the boundary in its original direction until it reaches the opposite boundary.
The light ray approaches the lower left face of the prism with an angle of incidence of 45 degrees (determined geometrically or by drawing a normal and measuring the angle). The critical angle for this boundary is approximately 37 degrees (invsin(1/1.70)). Since the angle of incidence is greater than the critical angle, TIR occurs and the light reflects according to the law of reflection. It then approaches the bottom right face of the prism.
Upon reaching the bottom right face of the prism, the light is incident with an angle of incidence of 45 degrees (determined geometrically or by drawing a normal and measuring the angle). Once more, since the angle of incidence is greater than the critical angle, TIR occurs and the light reflects according to the law of reflection. It then approaches the top face of the prism.
The light approaching the top face is traveling along the normal with an angle of incidence of 0 degrees. Similar to the original entry situation, the light will pass across the boundary and exit the prism without any refraction.
Part C
At the entry surface, the light ray approaches with an incident angle of 0 degrees. At this angle, no refraction occurs and the light ray continues across the boundary in its original direction until it reaches the opposite boundary.
At the opposite boundary, the angle of incidence is 45 degrees. This can be determined geometrically or by drawing a normal and measuring. The angle of refraction can be determined using Snell's law and the two indices of refraction. The angle of refraction is 35.6 degrees (invsin(1.4*sin(45 deg)/1.70)). The light ray in the second prism enters at a 35.6 degree angle from the normal and continues towards the right face of the prism as shown.
Once reaching the opposite side of the prism, the incident angle can be determined to be 54.4 degrees (determined geometrically or by drawing a normal and measuring the angle). The critical angle for this prism is approximately 36 degrees (invsin(1/1.70)). Since the incident angle is greater than the critical angle, TIR occurs and the light reflects according to the law of reflection. The light approaches the bottom face of the prism.
Once reaching the bottom face of the prism, the angle of incidence is 9.4 degrees (determined geometrically or by drawing a normal and measuring the angle). Using Snell's law, the angle of refraction can be determined to be approximately 16 degrees (invsin(1.7*sin(9.4 deg))). A normal is sketched and the refracted ray out of the prism is drawn at an angle of 16 degrees from the normal.
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
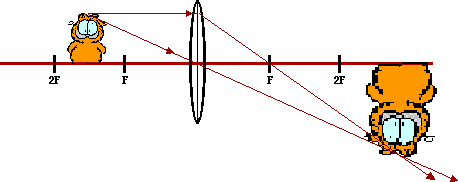
38. Construct ray diagrams to show where the images of the following objects are located. Draw in the complete image (approximated by an arrow) and describe its characteristics (real or virtual, enlarged or reduced in size, inverted or upright).
|
Answer:
In a ray diagram, pick a point on the extremities of the object and determine where the image of that point is located. Here, the head of the cat is selected and two incident rays and the corresponding refracted rays are drawn. The image point is where they intersect. The same can be done for the other extremity - the feet of the cat (a shortcut is to recognize that the image of an object on the principal axis will be located on the principal axis). Now draw in the complete image between the two image points. Often, the entire process is simplified by considering the object to simply be an arrow. Additional explanation and instruction on drawing ray diagrams is found on another page.
Whenever the object is located beyond the 2F point of a converging lens, the image is located between F and 2F on the other side of the lens; the image is real (located where refracted rays are intersecting), reduced in size, and inverted (and one might add, pretty darn cute).
|
 |
| Real |
Magnified |
Inverted |
|
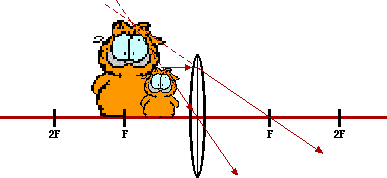
Answer:
In a ray diagram, pick a point on the extremities of the object and determine where the image of that point is located. Here, the head of the cat is selected and two incident rays and their corresponding refracted rays are drawn. The image point is where they intersect. The same can be done for the other extremity - the feet of the cat (a shortcut is to recognize that the image of an object on the principal axis will be located on the principal axis). Now draw in the complete image between the two image points. Often, the entire process is simplified by considering the object to simply be an arrow. Additional explanation and instruction on drawing ray diagrams is found on another page.
Whenever the object is located between the F and the 2F points of a converging lens, the image is located beyond 2F on the other side of the lens; the image is real (located where refracted rays are intersecting), magnified in size, and inverted.
|
|
|
Virtual
|
Magnified
|
Upright
|
|
Answer:
In a ray diagram, pick a point on the extremities of the object and determine where the image of that point is located. Here, the head of the cat is selected and two incident rays and their corresponding refracted rays are drawn. The image point is where they intersect. In the case, the refracted rays are diverging; the intersection point is found by tracing these refracted rays backwards until they do intersect. The same process can be done for the other extremity - the feet of the cat (a shortcut is to recognize that the image of an object on the principal axis will be located on the principal axis). Now draw in the complete image between the two image points. Often, the entire process is simplified by considering the object to simply be an arrow. Additional explanation and instruction on drawing ray diagrams is found on another page.
Whenever the object is located between the F point and the surface of a converging lens, the image is located on the same side of the lens; the image is virtual (located where refracted rays do not actually exist), magnified in size, and upright.
|
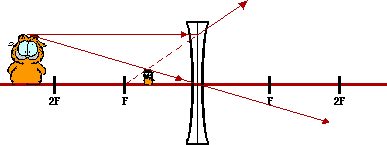
|
|
Virtual
|
Reduced
|
Upright
|
|
Answer:
In a ray diagram, pick a point on the extremities of the object and determine where the image of that point is located. Here, the head of the cat is selected and two incident rays and their corresponding refracted rays are drawn. The image point is where they intersect. In the case, the refracted rays are diverging; the intersection point is found by tracing these refracted rays backwards until they do intersect. The same process can be done for the other extremity - the feet of the cat (a shortcut is to recognize that the image of an object on the principal axis will be located on the principal axis). Now draw in the complete image between the two image points. Often, the entire process is simplified by considering the object to simply be an arrow. Additional explanation and instruction on drawing ray diagrams is found on another page.
Whenever the object is located anywhere in front of a diverging lens, the image is located on the same side of the lens; the image is virtual (located where refracted rays do not actually exist), reduced in size, and upright.
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
Part D: Problem-Solving
39. The speed of light in a vacuum is 3.00 x 108 m/s. Determine the speed of light through the following materials.
- air (n=1.00)
- ethanol (n=1.36)
- crown glass (n=1.52)
- zircon (n=1.91)
- diamond (n=2.42)
|
Answers:
For each of these questions, find the speed of light in the material by dividing the 3.00 x108 m/s by the index of refraction of the material. This yields the following results:
a. (3.00 x108 m/s)/1.00 = 3 x 108 m/s
b. (3.00 x108 m/s)/1.36 = 2.21 x 108 m/s
c. (3.00 x108 m/s)/1.52 = 1.97 x 108 m/s
d. (3.00 x108 m/s)/1.91 = 1.57 x 108 m/s
e. (3.00 x108 m/s)/2.42 = 1.24 x 108 m/s
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
4 0. Bruno is standing upon the edge of the water with his high-powered laser gun, waiting to zap the next visible fish with a burst of laser light. Frieda deFish, located a distance of 2.17 m out from shore, hopes to hide from view by ducking behind a small lily pad. If Bruno's laser is located 0.850-m above the ground and the lily pad is 1.39 m from shore, then to what depth below the water must Frieda descend in order to be hidden from view? (Given: nwater = 1.33)
0. Bruno is standing upon the edge of the water with his high-powered laser gun, waiting to zap the next visible fish with a burst of laser light. Frieda deFish, located a distance of 2.17 m out from shore, hopes to hide from view by ducking behind a small lily pad. If Bruno's laser is located 0.850-m above the ground and the lily pad is 1.39 m from shore, then to what depth below the water must Frieda descend in order to be hidden from view? (Given: nwater = 1.33)
|
Answer: 0.93 m
This is a problem which involves a combination of right triangle mathematics with Snell's law. As shown in the diagram above, the path of light and other imaginary lines break up the space above and below the water into a couple of right triangles. The game plan involves recognizing that right triangle mathematics must be used to find the angle of incidence and Snell's law can be used to find the angle of refraction. Once the angle of refraction is determined, right triangle trigonometry can be used to find the depth to which Frieda must descend. The two strategic triangles are shown in the diagram below. Angles are labeled to facilitate the discussion that follows.
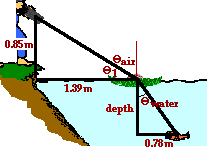
The problem is best solved systematically. Begin by finding theta1 in the diagram. Use the tangent relationship to state that theta1 = invtan(0.85 m/1.39 m) = 31.4 degrees. Since theta1 and the angle of incidence (Thetaair) add up to 90 degrees, the angle of incidence for the light ray approaching the water surface is 58.6 degrees.
Now use Snell's law to determine the angle of refraction. The equation can be set up as follows:
nair * sin(Thetaair) = nwater * sin(Thetawater)
1.00 * sin(58.6 deg) = 1.33 * sin(Thetawater)
1.00 * sin(58.6 deg) / 1.33 = sin(Thetawater)
39.9 degrees = Thetawater
Now attention can be turned to the lower triangle and the depth of the fish below the water can be determined. The length of the lower side of the triangle is simply the 2.17 m (distance of the fish from the shoreline) minus the 1.29 m (distance of the lily pad from the shoreline). The tangent function is used to find the side adjacent the 39.9 degree angle.
tan(39.9 degrees) = (0.78 m) / depth
Now using algebra, the equation can be evaluated for the depth:
depth = (0.78 m) / (tan(39.9 deg)) = 0.932 m
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
4 1. Frieda deFish, disturbed at Bruno's militance, pulls out a laser of her own. She temporarily ducks out from her cover and aims it upwards at an angle of 26.5-degrees at Bruno's nose. If Bruno's nose is 1.34-m above the water's edge and if Frieda is a distance of 0.91 m below the water's surface, then how far out from shore must Frieda be to have a direct hit?
1. Frieda deFish, disturbed at Bruno's militance, pulls out a laser of her own. She temporarily ducks out from her cover and aims it upwards at an angle of 26.5-degrees at Bruno's nose. If Bruno's nose is 1.34-m above the water's edge and if Frieda is a distance of 0.91 m below the water's surface, then how far out from shore must Frieda be to have a direct hit?
|
Answer: 1.44 m
Like the problem above, this is a problem which involves a combination of right triangle mathematics with Snell's law. As shown in the diagram above, the path of light and other imaginary lines break up the space above and below the water into a couple of right triangles. Once more, the game plan involves recognizing that Snell's law can be used to find the angle of refraction. Once the angle of refraction is determined, right triangle trigonometry can be used to find the length of the horizontal sides of the two strategic triangles. The two strategic triangles are shown in the diagram below. Angles are labeled to facilitate the discussion that follows.
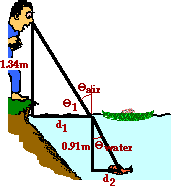
Begin by finding Thetaair in the diagram. This involves the use of Snell's law. The solution is below:
1.33*sin(26.5 deg) = 1.00*sin(Thetaair)
0.5934 = sin(Thetaair)
insin(0.5934) = Thetaair
36.4 degrees = Thetaair
Since Thetaair and Theta1 must add to 90 degrees, Theta1 is 53.6 degrees. This angle can be used to find the length of the horizontal side of the top triangle (d1). The solution involves the use of the tangent function as follows:
tan(53.6 degrees) = (1.34 m)/d1
d1 = (1.34 m)/tan(53.6 degrees)
d1 = 0.988 m
Now attention is focused on the bottom triangle in an effort to determine the length of the horizontal side of the bottom triangle (d2). The tangent function is used and the solution is as follows:
tan(26.5 deg) = d2 /(0.91 m)
d2 = tan(26.5 deg)*(0.91 m)
d2 = 0.45 m
Frieda is a distance of d1 + d2 out from shore. Summing the two distances yields 1.44 m.
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
42. Determine the critical angle for the following boundaries:
- air - crown glass (n=1.52)
- air - diamond (n=2.42)
- crown glass (n=1.52) - diamond (n=2.42)
- air - Lucite (n=1.40)
- air and a material through which light travels at a speed of 2.10 x 108 m/s
|
Answers:
The critical angle is the angle of incidence at which the angle of refraction is 90-degrees. So using Snell's law will result in the following derivation:
ni•sin(Critical Angle) = nr•sin(90 degrees)
sin(Critical Angle) = nr /ni
Critical Angle = invsin(nr/ni)
Since the critical angle only exists for light traveling from the more dense to the less dense medium, the higher n value would be placed in the denominator.
a. Critical angle = invsin(1.00/1.52) = 41.1 degrees.
b. Critical angle = invsin(1.00/2.42) = 24.4 degrees.
c. Critical angle = invsin(1.52/2.42) = 38.9 degrees.
d. Critical angle = invsin(1.00/1.40) = 45.6 degrees.
e. First find the index of refraction using n = (3x108 m/s)/(2.10x108 m/s) = 1.42; then use the equation Critical angle = invsin(1.00/1.42) = 44.4 degrees.
|
43. A lens produces an upright image of an object. The image is reduced in size by a factor of 3.00 when the object is a distance of 16.9 cm from the lens. Determine the focal length.
|
Answer: -8.45 cm
GIVEN:
do = 16.9 cm and hi = (+1/3.00)•ho
Use the magnification equation: M = hi/ho = -di/do = 1/3.00
Using the distance ratio in the magnification equation, it can be shown that
di = -(1/3.00)•do = -(1/3.00) •(16.9 cm) = -5.63 cm
Now use the lens equation to solve for the focal length:
1/f = 1/do + 1/di = 1/(16.9 cm) + 1/(-5.63 cm) = -0.118 / cm
f = 1/-0.118/cm = -8.45 cm
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
44. A thin lens has a focal point located 19.7 cm from the lens surface. When the object is placed at a specific location, the virtual image it produces is one-fourth the size of the object. Determine the object distance. (Careful of your sign on f.)
|
Answer: 59.1 cm
GIVEN:
f = -19.7 cm and hi = (+1/4)•ho
(Since the image is virtual and reduced, the lens must be a diverging lens; converging lenses produce magnified virtual images.)
Use the magnification equation: M = hi/ho = -di/do = 1/4 to develop an expression for image distance in terms of object distance:
-di/do = 1/4 ---> di = -0.25•do
Now substitute the expression for image distance into the lens equation to solve for the object distance:
1/(-19.7 cm) = 1/do + 1/(-0.25•do) = 1/do - 4/do = -3/do
do = -(3) • (-19.7 cm) = 59.1 cm
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
45. A thin lens has a focal point located 16.8 cm from the lens surface. Determine the object location which would produce an inverted image which is exactly five times larger than the object.
|
Answer: 20.16 cm
GIVEN:
f = 16.8 cm and hi = (-5.00) * ho
(Since the image is magnified and inverted, the lens must be a converging lens; only converging lenses produce magnified, inverted images. Since the image is inverted, a negative sign is placed into the equation describing the relative heights.)
Use the magnification equation: M = hi/ho = -di/do = -5.00 to develop an expression for image distance in terms of object distance:
-di/do = -5.00 ---> di = 5.00 * do
Now substitute the expression for image distance into the lens equation to solve for the object distance:
1/(16.8 cm) = 1/do + 1/(5.00*do) = 5.00/(5.00*do) + 1.00/(5.00*do) = 6.00/(5.00*do)
do = 1.20 * (16.8 cm) = 20.16 cm
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
46. A thin lens has a focal point located 16.8 cm from the lens surface. Determine the object location which would produce an upright image which is exactly five times larger than the object.
|
Answer: 13.4 cm
GIVEN:
f = 16.8 cm and hi = (5)•ho
(Since the image is magnified and upright, the lens must be a converging lens; only converging lenses produce magnified virtual images. Since the image is upright, a positive sign is placed into the equation describing the relative heights.)
Use the magnification equation: M = hi/ho = -di/do = 5 to develop an expression for image distance in terms of object distance:
-di/do = 5 ---> di = -5•do
Now substitute the expression for image distance into the lens equation to solve for the object distance:
1/(16.8 cm) = 1/do + 1/(-5do) = 5/5do - 1/5do = 4/5do
do = 4/5 • (16.8 cm) = 13.4 cm
|
[ #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #45 | #46 ]
Navigate to:
Review Session Home - Topic Listing
Refraction and Lenses - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#20 || #21-#34 || #35-#46
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Refraction and Lenses
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 6 of the series includes topics in Refraction and Lenses.
Visit: MOP the App Home || MOP the App - Part 6