Sound and Music Review
Navigate to:
Review Session Home - Topic Listing
Sound Waves and Music - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#9 || #10-#52 || #53-#64 || #65-#75
Part A: TRUE/FALSE
1. Which of the following statements are TRUE of sound waves? Identify all that apply.
- A sound wave is a mechanical wave.
- A sound wave is a means of transporting energy without transporting matter.
- Sound can travel through a vacuum.
- A sound wave is a pressure wave; they can be thought of as fluctuations in pressure with respect to time.
- A sound wave is a transverse wave.
- To hear the sound of a tuning fork, the tines of the fork must move air from the fork to one's ear.
- Most (but not all) sound waves are created by a vibrating object of some type.
- To be heard, a sound wave must cause a relatively large displacement of air (for instance, at least a cm or more) around an observer's ear.
|
Answer: ABD
a. TRUE - A sound wave transports its energy by means of particle interaction. A sound wave cannot travel through a vacuum. This makes sound a mechanical wave.
b. TRUE - Absolutely! Particles do not move from the source to the ear. Particles vibrate about a position; one particle impinges on its neighboring particle, setting it in vibrational motion about its own equilibrium position.
c. FALSE - Only electromagnetic waves can travel through a vacuum; mechanical waves such as sound waves require a particle-interaction to transport their energy. There are no particles in a vacuum.
d. TRUE - As particles move back and forth longitudinally, there are times when they are very close within a given region and other times that they are far apart within that same region. The close proximity of particles produces a high pressure region known as a compression; the distancing of particles within a region produces a low pressure region known as a rarefaction. Over time, a given region undergoes oscillations in pressure from a high to a low pressure and finally back to a high pressure.
e. FALSE - Never! Waves are either longitudinal or transverse. Longitudinal waves are those in which particles of the medium move in a direction parallel to the energy transport. And that is exactly how particles of the medium move as sound passes through it.
f. FALSE - It is the disturbance that moves from the tuning fork to one's ear. the particles of the medium merely vibrate back and forth about the same location, never really moving from that location to another location. This is true of all waves - they transport energy without actually transporting matter.
g. FALSE - All sound waves are created by vibrating objects of some sort.
h. FALSE - Quite surprisingly to many, most sounds which we are accustomed to hearing are characterized by particle motion with an amplitude on the order of 1 mm or less.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
2. Which of the following statements are TRUE of sound intensity and decibel levels? Identify all that apply.
- The intensity of a sound wave has units of Watts/meter.
- When a sound wave is said to be intense, it means that the particles are vibrating back and forth at a high frequency.
- Intense sounds are characterized by particles of the medium vibrating back and forth with a relatively large amplitude.
- Intense sounds are usually perceived as loud sounds.
- The ability of an observer to hear a sound wave depends solely upon the intensity of the sound wave.
- From the least intense to the most intense, humans have a rather narrow range of intensity over which sound waves can be heard.
- The intensity of sound which corresponds to the threshold of pain is one trillion times more intense than the sound which corresponds to the threshold of hearing.
- Two sounds which have a ratio of decibel ratings equal to 2.0. This means that the second sound is twice as intense as the first sound.
- Sound A is 20 times more intense than sound B. So if Sound B is rated at 30 dB, then sound A is rated at 50 dB.
- Sound C is 1000 times more intense than sound D. So if sound D is rated at 80 dB, sound C is rated at 110 dB.
- A machine produces a sound which is rated at 60 dB. If two of the machines were used at the same time, the decibel rating would be 120 dB.
- Intensity of a sound at a given location varies directly with the distance from that location to the source of the sound.
- If the distance from the source of sound is doubled then the intensity of the sound will be quadrupled.
- If the distance from the source of sound tripled, then the intensity of the sound will be increased by a factor of 6.
|
Answer: CDGJ
a. FALSE - Intensity is a power/area relationship and as such the units are typically Watts/meter2. The Watt is a unit of power and the meter2 is a unit of area.
b. FALSE - Intense sounds are simply sounds which carry energy outward from the source at a high rate. They are most commonly sound waves characterized by a high amplitude of movement. While frequency does effect one's perception of the loudness of a sound, it does not effect the intensity of a sound wave.
c. TRUE - An intense sound is the result of a large vibration of the source of sound that sets particles of the medium in motion with a high amplitude of movement about their usual rest position.
d. TRUE - Loudness is more of a subjective response to sound, dependent in part upon the quality of an observer's ears. Intensity is an objective characteristic of sound that can actually be measured in Watts/meter2. However, intense sounds will always be observed to be louder by an observer than less intense sounds.
e. FALSE - Not only must the sound be intense enough to cause an audible disturbance of the mechanisms of the ear, it also must fall within the human frequency range of 20 Hz to 20000 Hz.
f. FALSE - Humans actually have a phenomenal range of intensities to which they are sensitive to. The intensity of the sound at the threshold of pain is one-trillion times more intense than the sound at the threshold of hearing. That's quite a range.
g. TRUE - The threshold of pain has an intensity of 1 W/m2 and the threshold of hearing has an intensity of 1.0 x 10-12 W/m2. That's a ratio of one trillion.
h. FALSE - No! Since the decibel scale is based on a logarithmic function, this is simply not the case.
i. FALSE - Two sounds separated by 20 dB on the decibel scale have intensity ratios of 100:1. If one sound is 20 times more intense than another sound, then it is 13 dB higher on the decibel scale [ that comes from 10*log(20) ].
j. TRUE - Always remember that a decibel rating is based on the logarithmic function. A sound which is 1000 times (103 times) more intense than another sound is 3 bels or 30 dBels greater on the decibel scale.
k. FALSE - Two machines would produce twice the intensity; but when converted to the logarithmic scale of decibels, there decibel rating would differ by 3 dB.
l. FALSE - Intensity varies inversely with distance from the source. To be more specific, it varies inversely with the square of the distance.
m. FALSE - If the distance from the source is doubled, then the intensity is decreased by a factor of four.
n. FALSE - If the distance from the source is tripled, then the intensity is decreased by a factor of nine.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
3. Which of the following statements are TRUE of the speed of sound? Identify all that apply.
- The speed of a sound wave depends upon its frequency and its wavelength.
- In general, sound waves travel fastest in solids and slowest in gases.
- Sound waves travel fastest in solids (compared to liquids and gases) because solids are more dense.
- The fastest which sound can move is when it is moving through a vacuum.
- If all other factors are equal, a sound wave will travel fastest in the most dense materials.
- A highly elastic material has a strong tendency to return to its original shape if stressed, stretched, plucked or somehow disturbed.
- A more rigid material such as steel has a higher elasticity and therefore sound tends to move through it at high speeds.
- The speed of sound moving through air is largely dependent upon the frequency and intensity of the sound wave.
- A loud shout will move faster through air than a faint whisper.
- Sound waves would travel faster on a warm day than a cool day.
- The speed of a sound wave would be dependent solely upon the properties of the medium through which it moves.
- A shout in a canyon produces an echo off a cliff located 127 m away. If the echo is heard 0.720 seconds after the shout, then the speed of sound through the canyon is 176 m/s.
- The speed of a wave within a guitar string varies inversely with the tension in the string.
- The speed of a wave within a guitar string varies inversely with the mass per unit length of the string.
- The speed of a wave within a guitar string will be doubled if the tension of the string is doubled.
- An increase in the tension of a guitar string by a factor of four will increase the speed of a wave in the string by a factor of two.
- An increase in the linear mass density of a guitar string by a factor of four will increase the speed of a wave in the string by a factor of two.
|
Answer: BFGJKNP
a. FALSE - The speed of a wave is calculated by the product of the frequency and wavelength. However, it does not depend upon the frequency and the wavelength. An alteration in the frequency or the wavelength will not alter the speed.
b. TRUE - For the same material, speed is greatest in materials in which the elastic properties are greatest. Despite the greater density of solids, the speed is greatest in solids, followed by liquids, followed by gases.
c. FALSE - Sound waves travel faster in solids because the particles of a solid have a greater elastic modulus. That is to say that a disturbance of a particle from its rest position in a solid leads to a rapid return to its rest position and as such an ability to rapidly transmit the energy to the next particle.
d. FALSE - Sound is a mechanical wave which moves due to particle interaction. There are no particles in a vacuum so sound can not move through a vacuum.
e. FALSE - Sound waves (like all waves) will travel slower in more dense materials (assuming all other factors are equal).
f. TRUE - This is the definition of elasticity. Elasticity is related to the ability of the particles of a material to return to their original position if displaced from it.
g. TRUE - A more rigid material is characterized by particles which quickly return to their original position if displaced from it. Sound moves fastest in such materials.
h. FALSE - The speed of sound through a material is dependent upon the properties of the material, not the characteristics of the wave.
i. FALSE - A loud shout will move at the same speed as a whisper since the speed of sound is independent of the characteristics of the sound wave and dependent upon the properties of the material through it is moving.
j. TRUE - The speed of sound through air is dependent upon the temperature of the air.
k. TRUE - This is a big principle. Know it.
l. FALSE - Speed is distance traveled per time. For this case, the sound travels a distance of 254 m (to the cliff and back) in 0.720 seconds. That computes to 353 m/s.
m. FALSE - For a guitar string, the equation for the speed of waves is v = SQRT (Ftens/mu). From the equation, it is evident that an increase in tension will result in an increase in the speed; they are directly related.
n. TRUE - For a guitar string, the equation for the speed of waves is v = SQRT (Ftens/mu). From the equation, it is evident that an increase in mass per unit length (mu) will result in an decrease in the speed; they are inversely related.
o. FALSE - The speed of a wave in a guitar string varies directly with the square root of the tension. If the tension is doubled, then the speed of sound will increase by a factor of the square root of two.
p. TRUE - The speed of a wave in a string is directly related to the square root of the tension in the string. So the speed will be changed by the square root of whatever factor the tension is changed.
q. FALSE - An increase in the linear mass density by a factor of four will decrease the speed by a factor of 2. The speed is inversely related to the square root of the linear density.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
4. Which of the following statements are TRUE of the frequency of sound and the perception of pitch? Identify all that apply.
- A high pitched sound has a low wavelength.
- A low-pitched sound is a sound whose pressure fluctuations occur with a low period.
- If an object vibrates at a relatively high frequency, then the pitch of the sound will be low.
- The frequency of a sound will not necessarily be the same as the frequency of the vibrating object since sound speed will be altered as the sound is transmitted from the object to the air and ultimately to your ear.
- Two different guitar strings are used to produce a sound. The strings are identical in terms of material, thickness and the tension to which they are pulled. Yet string A is shorter than string B. Therefore, string A will produce a lower pitch.
- Both low- and high-pitched sounds will travel through air at the same speed.
- Doubling the frequency of a sound wave will halve the wavelength but not alter the speed of the wave.
- Tripling the frequency of a sound wave will decrease the wavelength by a factor of 6 and alter the speed of the wave.
- Humans can pretty much hear a low-frequency sound as easily as a high-frequency sound.
- Ultrasound waves are those sound waves with frequencies less than 20 Hz.
|
Answer: AFG
a. TRUE - High pitch corresponds to a sound with high frequency and therefore low wavelength.
b. FALSE - Low pitched sound have a low frequency. Frequency is inversely related to period. So low pitched sounds have a high period. That is, the time for the vibrations to undergo one complete cycle is large for a low frequency (or low pitch) sound.
c. FALSE - Pitch is a subjective response of the ear to sound. Frequency is an objective measure of how often the sound undergoes an oscillation from high to low pressure. The two are related in the sense that a sound with a high frequency will be perceived as a sound with a high pitch.
d. FALSE - As waves (of any type) are transmitted from one medium to another, the speed and the wavelength can be altered, but the frequency will not be changed. Thus, the frequency of the source is the frequency of the sound waves which impinge upon the ear.
e. FALSE - The strings are identical in terms of their properties; this means that waves travel at the same speed through each. Yet string A is shorter than string B, so the wavelengths of waves are shortest in string A. As such, the frequencies are greatest for string A and it is observed to produce sounds of higher pitch.
f. TRUE - The speed at which waves travel through air is dependent upon the properties of the air and not the properties of the wave.
g. TRUE - Frequency and wavelength are inversely related; doubling one will halve the other. Yet the speed of a wave is independent of each.
h. FALSE - Tripling the frequency of a sound wave will make wavelength decrease by a factor of 3 but not alter the speed of a wave.
i. FALSE - The response of the ear to sound is dependent in part on the frequency of the sound. A higher pitch sound of the same intensity is generally heard to be louder than a lower pitch sound of the same intensity.
j. FALSE - Ultrasound waves are waves which have a frequency beyond the human range of audible frequencies - above 20000 Hz.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
5. Which of the following statements are TRUE of standing wave patterns? Identify all that apply.
- A standing wave pattern is formed as a result of the interference of two or more waves.
- When a standing wave pattern is established, there are portions of the medium which are not disturbed.
- A standing wave is really not a wave at all; it is a pattern resulting from the interference of two or more waves which are traveling through the same medium.
- A standing wave pattern is a regular and repeating vibrational pattern established within a medium; it is always characterized by the presence of nodes and antinodes.
- An antinode on a standing wave pattern is a point which is stationary; it does not undergo any displacement from its rest position.
- For every node on a standing wave pattern, there is a corresponding antinode; there are always the same number of each.
- When a standing wave pattern is established in a medium, there are alternating nodes and antinodes, equally spaced apart across the medium.
|
Answer: ABCDG
a. TRUE - Interference results when two (or more) waves interfere to produce a regular and repeating pattern of nodes and antinodes. The presence of the nodes standing still along the medium at the same position is what gives it its name of "standing" wave.
b. TRUE - Standing wave patterns are characterized by the presence of nodes - points of no disturbance.
c. TRUE - This is correct. When a standing wave pattern is being observed, it is an interference pattern - a pattern of the medium resulting from two or more waves interfering to produce the very visible pattern.
d. TRUE - This is probably a good definition of a standing wave pattern.
e. FALSE - Nodes are points which are stationary and undergoing no displacement. The antinodal positions of a standing wave pattern undergo oscillation from a maximum positive displacement to a maximum negative displacement.
f. FALSE -This would be a true statement for standing wave patterns formed in closed-end resonance air columns. Yet for guitar strings and open end air columns, there is always one more node than antinode.
g. TRUE - This is a good way to describe what is seen in the pattern.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
6. Which of the following statements are TRUE of the concept of resonance? Identify all that apply.
- A musical instrument can play any frequency imaginable.
- All musical instruments have a natural frequency or set of natural frequencies at which they will vibrate; each frequency corresponds to a unique standing wave pattern.
- The result of two objects vibrating in resonance with each other is a vibration of larger amplitude.
- Objects which share the same natural frequency will often set each other into vibrational motion when one is plucked, strummed, hit or otherwise disturbed. This phenomenon is known as a forced resonance vibration.
- A vibrating tuning fork can set a second tuning fork into resonant motion.
- The resonant frequencies of a musical instrument are related by whole number ratios.
|
Answer: BCDE(mostly)F
a. FALSE - An instrument which is truly musical can only play a specific set of frequencies, each one corresponding to a standing wave pattern with which that instrument can vibrate. (Of course, one could make a case that by modifying properties of the instrument, small adjustments could be made in the speed at which the waves might move and thus allow the instrument to produce about any frequency imaginable.)
b. TRUE - The frequencies at which an instrument would naturally vibrate are known as its harmonics. Each frequency corresponds to a unique standing wave pattern.
c. TRUE - Resonance results in a big vibration because two waves are now interfering in a regular manner to produce a resultant wave with a large amplitude of vibration.
d. TRUE - This is a good definition of resonance vibrations.
e. TRUE - This can happen provided that the two tuning forks have the same natural frequency and that they are somehow connected (for instance by air).
f. TRUE - The frequencies at which an instrument would naturally vibrate are known as its harmonics. The frequency of each harmonic is a whole number multiple of the fundamental frequency. As such, every frequency in the set of natural frequency is related by whole number rations.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
7. Which of the following statements are TRUE of the harmonics and standing wave patterns in guitar strings? Identify all that apply.
- The fundamental frequency of a guitar string is the highest frequency at which the string vibrates.
- The fundamental frequency of a guitar string corresponds to the standing wave pattern in which there is a complete wavelength within the length of the string.
- The wavelength for the fundamental frequency of a guitar string is 2.0 m.
- The wavelength for the second harmonic played by a guitar string is two times the wavelength of the first harmonic.
- The standing wave pattern for the fundamental played by a guitar string is characterized by the pattern with the longest possible wavelength.
- If the fundamental frequency of a guitar string is 200 Hz, then the frequency of the second harmonic is 400 Hz.
- If the frequency of the fifth harmonic of a guitar string is 1200 Hz, then the fundamental frequency of the same string is 6000 Hz.
- As the frequency of a standing wave pattern is tripled, its wavelength is tripled.
- If the speed of sound in a guitar string is 300 m/s and the length of the string is 0.60 m, then the fundamental frequency will be 180 Hz.
- As the tension of a guitar string is increased, the fundamental frequency produced by that string is decreased.
- As the tension of a guitar string is increased by a factor of 2, the fundamental frequency produced by that string is decreased by a factor of 2.
- As the linear density of a guitar string is increased, the fundamental frequency produced by the string is decreased.
- As the linear density of a guitar string is increased by a factor 4, the fundamental frequency produced by the string is decreased by a factor of 2.
|
Answer: EFLM
a. FALSE - The fundamental frequency is the lowest possible frequency which an instrument will play.
b. FALSE - For a guitar string, the standing wave pattern for the fundamental frequency is one in which there is one-half wavelength within the length of the string.
c. FALSE - The wavelength for the fundamental frequency is two times the length of the string (not 2.0 m).
d. FALSE - The wavelength of the second harmonic is one-half the length of the wavelength of the fundamental (the frequency of the second harmonic is twice the frequency of the fundamental).
e. TRUE - The fundamental frequency is the lowest possible frequency and the longest possible wavelength with which an instrument will vibrate.
f. TRUE -The frequency of the nth harmonic is n times larger than the frequency of the fundamental or first harmonic.
g. FALSE - The frequency of the fundamental would be 240 Hz if the frequency of the fifth harmonic is 1200 Hz.
h. FALSE - If the frequency is tripled, then the wavelength is one-third as much.
i. FALSE - The fundamental frequency would be 250 Hz. The wavelength of the fundamental is two times the length of the string - 1.2 m. And the frequency of the fundamental is the speed divided by the wavelength of the fundamental.
j. FALSE - As the tension of a guitar string is increased, the speed of vibrations in the string is increased and the frequency will be increased.
k. FALSE - If the tension in a guitar string is increased by a factor of 2, then the speed of vibrations in the string will be increased by a factor of the square root of 2 (1.41) and the frequency will be increased by a factor of 1.41.
l. TRUE - If the linear density of a guitar string is increased, then the speed of vibrations in the string will be decreased and the frequency will be decreased.
m. TRUE - If the linear density of a guitar string is increased by a factor of 4, then the speed of vibrations in the string will be decreased by a factor of the square root of 4 (2.0) and the frequency will be decreased by a factor of 2.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
8. Which of the following statements are TRUE of the harmonics and standing wave patterns in air columns? Identify all that apply.
- The speed of the waves for the various harmonics of open-end air columns are whole number multiples of the speed of the wave for the fundamental frequency.
- Longer air columns will produce lower frequencies.
- The pitch of a sound can be increased by shortening the length of the air resonating inside of an air column.
- An open end of an air column allows air to vibrate a maximum amount whereas a closed end forces air particles to behave as nodes.
- Open-end air columns have antinodes positioned at each end while closed-end air columns have nodes positioned at each end.
- Closed-end air columns can only produce odd-numbered harmonics.
- Open-end air columns can only produce even-numbered harmonics.
- A closed-end air column that can play a fundamental frequency of 250 Hz cannot play 500 Hz.
- An open-end air column that can play a fundamental frequency of 250 Hz cannot play 750 Hz.
- A closed-end air column has a length of 20 cm. The wavelength of the first harmonic is 5 cm.
- An open-end air column has a length of 20 cm. The wavelength of the first harmonic is 10 cm.
- Air column A is a closed-end air column. Air column B is an open-end air column. Air column A would be capable of playing lower pitches than air column B.
- The speed of sound in air is 340 m/s. An open-end air column has a length of 40 cm. The fundamental frequency of this air column is approximately 213 Hz.
- The speed of sound in air is 340 m/s. A closed-end air column has a length of 40 cm. The fundamental frequency of this air column is approximately 213 Hz.
- If an open-end air column has a fundamental frequency of 250 Hz, then the frequency of the fourth harmonic is 1000 Hz.
- If a closed-end air column has a fundamental frequency of 200 Hz, then the frequency of the fourth harmonic is 800 Hz.
|
Answer: BCDFHLNO
a. FALSE - It is the frequency (not the speed) of the various harmonics which are whole number multiples of the fundamental frequency.
b. TRUE - Assuming that two air columns are of the same type (both open- or both closed), the standing wave patterns of the longer air column would have longer wavelengths and thus lower frequencies and pitch.
c. TRUE - As the length of an air column is shortened, the wavelengths are decreased and the frequencies are increased.
d. TRUE - This is exactly the case and is clearly portrayed in the standing wave patterns which are constructed for air columns.
e. FALSE - A closed-end air column is an air column with one end open and one end closed. It is the closed end which is characterized by a nodal position but the open end is characterized by an antinode.
f. TRUE - Closed-end air columns produce a first, third, fifth, seventh, etc. harmonic - all odd numbers.
g. FALSE - Open-end air columns can produce all harmonics - first, second, third, fourth, etc.
h. TRUE - If a closed-end air column has a fundamental frequency of 250 Hz, then the other frequencies in the set of natural frequencies are 750 Hz, 1250 Hz, 1750 Hz, etc. It can only have odd-numbered harmonics.
i. FALSE - If an open-end air column has a fundamental frequency of 250 Hz, then the other frequencies in the set of natural frequencies are 500 Hz, 750 Hz, 1000 Hz, 1250 Hz, etc. An open-end air column can produce all the harmonics.
j. FALSE - The wavelength of the first harmonic of a closed-end air column is four times the length of the air column - 80 cm.
k. FALSE - The wavelength of the first harmonic of an open-end air column is two times the length of the air column - 40 cm.
l. TRUE (sort of) - For the same length (the sort of part), a closed-end air column would have standing waves which are longer and therefore have frequencies which are lower.
m. FALSE - If the length of this open-end air column is 40 cm, then the wavelength of the fundamental is 0.80 m. The frequency of the fundamental is (340 m/s)/(0.8 m) = 425 Hz.
n. TRUE - If the length of this closed-end air column is 40 cm, then the wavelength of the fundamental is 1.60 m. The frequency of the fundamental is (340 m/s)/(1.6 m) = 213 Hz.
o. TRUE - The frequency of the fourth harmonic is four times the frequency of the first harmonic.
p. FALSE - A closed-end air column cannot have a fourth harmonic; there are only odd-numbered frequencies.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
9. Which of the following statements are TRUE of sound interference and beats? Identify all that apply.
- Beats result when two sounds of slightly different frequencies interfere.
- Beats are characterized by a sound whose frequency is rapidly fluctuating between a high and a low pitch.
- Two sounds with a frequency ratio of 2:1 would produce beats with a beat frequency of 2 Hz.
- Two tuning forks are sounding out at slightly different frequencies - 252 Hz and 257 Hz. A beat frequency of 5 Hz will be heard.
- A piano tuner is using a 262 Hz tuning fork in an effort to tune a piano string. She plucks the string and the tuning fork and observes a beat frequency of 2 Hz. Therefore, she must lower the frequency of the piano string by 2 Hz.
|
Answer: AD
a. TRUE - This is the number one criteria for the formation of audible beats.
b. FALSE - Beats are characterized by sounds which are rapidly oscillating between high and low levels of loudness due to fluctuations in the amplitude of the resulting wave.
c. FALSE - Two sounds with a frequency difference (not ratio) of 2 Hz will produce a bear frequency of 2 Hz.
d. TRUE - The beat frequency is the frequency at which the amplitude of the oscillations increase and decrease. This beat frequency is always the difference in frequency of the two sounds which interfere to create the beats.
e. FALSE - She must either lower or increase the frequency of the piano string by 2 Hz.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
Part B: Multiple Choice
10. What type of wave is produced when the particles of the medium are vibrating to and fro in the same direction of wave propagation?
|
a. longitudinal wave.
|
b. sound wave.
|
c. standing wave.
|
d. transverse wave.
|
|
Answer: A
This is the definition of a longitudinal wave. A longitudinal wave is a wave in which particles of the medium vibrate to and fro in a direction parallel to the direction of energy transport.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
11. When the particles of a medium are vibrating at right angles to the direction of energy transport, the type of wave is described as a _____ wave.
|
a. longitudinal
|
b. sound
|
c. standing
|
d. transverse
|
|
Answer: D
This is the definition of a transverse wave. A transverse wave is a wave in which particles of the medium vibrate to and fro in a direction perpendicular to the direction of energy transport.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
12. A transverse wave is traveling through a medium. See diagram below. The particles of the medium are moving.
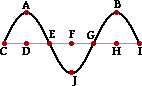
|
a. parallel to the line joining AD.
|
b. along the line joining CI.
|
|
c. perpendicular to the line joining AD.
|
d. at various angles to the line CI.
|
|
e. along the curve CAEJGBI.
|
|
|
Answer: A
In transverse waves, particles of the medium vibrate to and fro in a direction perpendicular to the direction of energy transport. In this case, that would be parallel to the line AD.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
13. If the energy in a longitudinal wave travels from south to north, the particles of the medium ____.
|
a. move from north to south, only.
|
b. vibrate both north and south.
|
|
c. move from east to west, only.
|
d. vibrate both east and west.
|
|
Answer: B
In longitudinal waves, particles of the medium vibrate to and from in a direction parallel to the direction of energy transport. If the particles only moved north and not back south, then the particles would be permanently displaced from their rest position; this is not wavelike.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
14. The main factor which effects the speed of a sound wave is the ____.
|
a. amplitude of the sound wave
|
b. intensity of the sound wave
|
|
c. loudness of the sound wave
|
d. properties of the medium
|
|
e. pitch of the sound wave
|
|
|
Answer: D
The speed of a wave is dependent upon the properties of the medium and not the properties of the wave.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
15. As a wave travels into a medium in which its speed increases, its wavelength ____.
|
a. decreases
|
b. increases
|
c. remains the same
|
|
Answer: B
As a wave crosses a boundary into a new medium, its speed and wavelength change while its frequency remains the same. If the speed increases, then the wavelength must increase as well in order to maintain the same frequency.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
16. As a wave passes across a boundary into a new medium, which characteristic of the wave would NOT change?
|
a. speed
|
b. frequency
|
c. wavelength
|
|
Answer: B
As a wave crosses a boundary into a new medium, its speed and wavelength change while its frequency remains the same. This is true of all waves as they pass from one medium to another medium.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
17. The ____ is defined as the number of cycles of a periodic wave occurring per unit time.
|
a. wavelength
|
b. period
|
c. amplitude
|
d. frequency
|
|
Answer: D
This is a basic definition which you should know and be able to apply.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
18. Many wave properties are dependent upon other wave properties. Yet, one wave property is independent of all other wave properties. Which one of the following properties of a wave is independent of all the others?
|
a. wavelength
|
b. frequency
|
c. period
|
d. velocity
|
|
|
Answer: D
The speed (or velocity) of a wave is dependent upon the properties of the medium through which it moves, not upon the properties of the wave itself.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
19. Consider the motion of waves in a wire. Waves will travel fastest in a ____ wire.
|
a. tight and heavy
|
b. tight and light
|
c. loose and heavy
|
d. loose and light
|
|
Answer: B
The speed of a wave in a wire is given by the equation
v = SQRT (Ftens/mu)
where Ftens is the tension of the wire and a measure of how tight it is pulled and mu is the linear density of the wire and a measure of how light it is on a per meter basis. Tighter wires allow for faster speeds. Light wires allow for faster speeds.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
20. TRUE or FALSE:
The SI unit for frequency is hertz.
|
Answer: A
Know this like the back of your hand (assuming you know the back of your hand well).
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
21. TRUE or FALSE:
Doubling the frequency of a sound source doubles the speed of the sound waves which it produces.
|
Answer: B
Don't be fooled. Wave speed may equal frequency*wavelength. Yet doubling the frequency only halves the wavelength; wave speed remains the same. To change the wave speed, the medium would have to be changed.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
22. A sound wave has a wavelength of 3.0 m. The distance between the center of a compression and the center of the next adjacent rarefaction is ____.
|
a. 0.75 m.
|
b. 1.5 m.
|
c. 3.0 m.
|
d. 6.0 m.
|
|
e. impossible to calculate without knowing frequency.
|
|
Answer: B
The wavelength of a wave is measured as the distance between any two corresponding points on adjacent wave. For a sound wave, that would be from compression to the next adjacent compression. If that distance is 3.0 meters, then the distance from compression to the next adjacent rarefaction is 1.5 m.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
23. Which one of the following factors determines the pitch of a sound?
a. The amplitude of the sound wave
b. The distance of the sound wave from the source
c. The frequency of the sound wave
d. The phase of different parts of the sound wave
e. The speed of the sound wave
|
Answer: C
The pitch of a sound wave is related to the frequency of the sound wave.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
24. A certain note is produced when a person blows air into an organ pipe. The manner in which one blows on a organ pipe (or any pipe) will effect the characteristics of the sound which is produced. If the person blows slightly harder, the most probable change will be that the sound wave will increase in ____.
|
a. amplitude
|
b. frequency
|
c. pitch
|
d. speed
|
e. wavelength
|
|
Answer: A
If you put more energy into the wave - i.e., blow harder - then the amplitude of the waves will be greater. Energy and amplitude are related.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
25. A vibrating object with a frequency of 200 Hz produces sound which travels through air at 360 m/s. The number of meters separating the adjacent compressions in the sound wave is ____.
|
a. 0.90
|
b. 1.8
|
c. 3.6
|
d. 7.2
|
e. 200
|
|
Answer: B
Let w=wavelength; then v = w*f. In this problem, it is given that v=360 m/s and f = 200 Hz. Substitution and algebra yields w = v/f = 1.8 m. The question asks for the wavelength - i.e., the distance between adjacent compressions.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
26. Consider the diagram below of several circular waves created at various times and locations. The diagram illustrates ____.
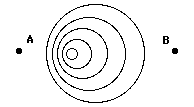
|
a. interference
|
b. diffraction
|
c. the Doppler effect.
|
d. polarization
|
|
Answer: C
The Doppler effect or Doppler shift occurs when a source of waves is moving with respect to an observer. The observer observes a different frequency of waves than that emitted by the source. This is due to the fact that the waves are compressed together into less space in the direction in which the source is heading.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
27. In the diagram above, a person positioned at point A would perceive __________ frequency as the person positioned at point B.
|
a. a higher
|
b. a lower
|
c. the same
|
|
Answer: A
The Doppler effect or Doppler shift occurs when a source of waves is moving with respect to an observer. The observer observes a different frequency of waves than that emitted by the source. If the source and observer are approaching, then the observed frequency is higher than the emitted frequency. If the source and observer are moving away from each other, the observer observes a lower frequency than the emitted frequency.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
28. A girl moves away from a source of sound at a constant speed. Compared to the frequency of the sound wave produced by the source, the frequency of the sound wave heard by the girl is ____.
|
a. lower.
|
b. higher.
|
c. the same.
|
|
Answer: A
The Doppler effect or Doppler shift occurs when a source of waves is moving with respect to an observer. The observer observes a different frequency of waves than that emitted by the source. If the source and observer are moving away, then the observed frequency is lower than the emitted frequency.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
29. An earth-based receiver is detecting electromagnetic waves from a source in outer space. If the frequency of the waves are observed to be increasing, then the distance between the source and the earth is probably ____.
|
a. decreasing.
|
b. increasing.
|
c. remaining the same.
|
|
Answer: A
The Doppler effect or Doppler shift occurs when a source of waves is moving with respect to an observer. The observer observes a different frequency of waves than that emitted by the source. If the source and observer are approaching, then the observed frequency is higher than the emitted frequency. If the source and observer are approaching, then the distance between them is decreasing.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
30. As two or more waves pass simultaneously through the same region, ____ can occur.
|
a. refraction
|
b. diffraction
|
c. interference
|
d. reflection
|
|
Answer: C
Interference is the meeting of two or more waves when passing along the same medium - a basic definition which you should know and be able to apply.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
31. TRUE or FALSE:
If two crests meet while passing through the same medium, then constructive interference occurs.
|
Answer: A
Yes! Or when a trough meets a trough or whenever two waves displaced in the same direction - both up or both down - meet.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
32. A node is a point along a medium where there is always ____.
|
a. a crest meeting a crest
|
b. a trough meeting a trough
|
c. constructive interference
|
|
d. destructive interference
|
e. a double rarefaction.
|
|
|
Answer: D
A node is a point along the medium of no displacement. The point is not displaced because destructive interference occurs at this point.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
33. TRUE or FALSE:
It is possible that one vibrating object can set another object into vibration if the natural frequencies of the two objects are the same.
|
Answer: A
Yes! This is known as resonance. Resonance occurs when a vibrating object forces another object into vibration at the same natural frequency. A basic definition of a commonly discussed phenomenon.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
34. An object is vibrating at its natural frequency. Repeated and periodic vibrations of the same natural frequency impinge upon the vibrating object and the amplitude of its vibrations are observed to increase. This phenomenon is known as ____.
|
a. beats
|
b. fundamental
|
c. interference
|
d. overtone
|
e. resonance
|
|
Answer: E
Resonance occurs when a vibrating object forces another object into vibration at the same natural frequency and thus increase the amplitude of its vibrations. A basic definition of a commonly discussed phenomenon.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
35. A standing wave experiment is performed to determine the speed of waves in a rope. The standing wave pattern shown below is established in the rope. The rope makes 90.0 complete vibrational cycles in exactly one minute. The speed of the waves is ____ m/s.
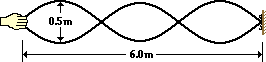
|
a. 3.0
|
b. 6.0
|
c. 180
|
d. 360
|
e. 540
|
|
Answer: B
Ninety vibrations in 60.0 seconds means a frequency of 1.50 Hz. The diagram shows 1.5 waves in 6.0-meters of rope; thus, the wavelength (w) is 4 meters. Now use the equation v=f*w to calculate the speed of the wave. Proper substitution yields 6.0 m/s.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
36. Standing waves are produced in a wire by vibrating one end at a frequency of 100. Hz. The distance between the 2nd and the 5th nodes is 60.0 cm. The wavelength of the original traveling wave is ____ cm.
|
a. 50.0
|
b. 40.0
|
c. 30.0
|
d. 20.0
|
e. 15.0
|
|
Answer: B
The frequency is given as 100. Hz and the wavelength can be found from the other givens. The distance between adjacent nodes is one-half a wavelength; thus the 60.0-cm distance from 2nd to 5th node is 1.50 wavelengths. For this reason, the wavelength is 40.0 cm.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | [ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
37. Consider the standing wave pattern shown below. A wave generated at the left end of the medium undergoes reflection at the fixed end on the right side of the medium. The number of antinodes in the diagram is
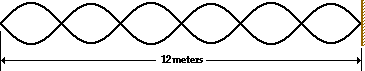
|
a. 3.0
|
b. 5.0
|
c. 6.0
|
d. 7.0
|
e. 12
|
|
Answer: C
An antinode is a point on the medium which oscillates from a large + to a large - displacement. Count the number of these points - there are 6 - but do not count them twice.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
38. The standing wave pattern in the diagram above is representative of the ____ harmonic.
|
a. third
|
b. fifth
|
c. sixth
|
d. seventh
|
e. twelfth
|
|
Answer: C
If there are six antinodes in the standing wave pattern, then it is the sixth harmonic.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
39. The distance between successive nodes in any standing wave pattern is equivalent to ____ wavelengths.
|
a. 1/4
|
b. 1/2
|
c. 3/4
|
d. 1
|
e. 2.
|
|
Answer: B
Draw a standing wave pattern or look at one which is already drawn; note that the nodes are positioned one-half of a wavelength apart. This is true for guitar strings and for both closed-end and open-end resonance tubes.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
40. A vibrating tuning fork is held above a closed-end air column, forcing the air into resonance. If the sound waves created by the tuning fork have a wavelength of W, then the length of the air column could NOT be ____.
|
a. 1/4 W
|
b. 2/4 W
|
c. 3/4 W
|
d. 5/4 W
|
e. 7/4 W
|
|
Answer: B
Review your diagrams for the standing wave patterns in closed end air columns; note that resonance occurs when the length of the air column is 1/4, 3/4, 5/4, 7/4, ... of a wavelength. Because these possible resonant lengths are characterized by an odd-numbered numerator, it is said that closed-end air columns only produce odd harmonics.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
41. TRUE or FALSE:
A vibrating tuning fork is held above an air column, forcing the air into resonance. The length of the air column is adjusted to obtain various resonances. The sound waves created by the tuning fork have a wavelength of W. The difference between the successive lengths of the air column at which resonance occurs is 1/2 W.
|
Answer: A
True! Observe the standing wave patterns and the length-wavelength relationships which we have discussed for both open- and closed-end tubes. In each case, resonance occurs at lengths of tubes which are separated by one-half wavelength; e.g., Closed: .25*W, .75*wW 1.25*W, 1.75*W... Open: .5*W, 1.0*W, 1.5*W, 2.0*W, ...
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
42. TRUE or FALSE:
An organ pipe which is closed at one end will resonate if its length is equal to one-half of the wavelength of the sound in the pipe.
|
Answer: B
It will resonate if the length is equal to the one-fourth (or three-fourths, or five-fourths or ...) the wavelength of the sound wave.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
43. A 20.0-cm long pipe is covered at one end in order to create a closed-end air column. A vibrating tuning fork is held near its open end, forcing the air to vibrate in its first harmonic. The wavelength of the standing wave pattern is ____.
|
a. 5.0 cm
|
b. 10.0 cm
|
c. 20.0 cm
|
d. 40.0 cm
|
e. 80.0 cm
|
|
Answer: E
This is a closed-end air column. If you draw the standing wave pattern for the first harmonic, you will notice that the wavelength is four times the length of the air column. Thus take the length of 20.0 cm and multiply by 4.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
44. A stretched string vibrates with a fundamental frequency of 100. Hz. The frequency of the second harmonic is ____.
|
a. 25.0 Hz
|
b. 50.0 Hz
|
c. 100. Hz
|
d. 200. Hz
|
e. 400. Hz
|
|
Answer: D
The frequency of the nth harmonic is n times the frequency of the first harmonic where n is an integer. Thus, f2 = 2*f1 = 2*100. Hz = 200. Hz.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
45. A 40.0-cm long plastic tube is open at both ends and resonating in its first harmonic. The wavelength of the sound which will produce this resonance is ____.
|
a. 10.0 cm
|
b. 20.0 cm
|
c. 40.0 cm
|
d. 80.0 cm
|
e. 160 cm
|
|
Answer: D
For an open-end air column, the length of the column is 0.5*wavelength. This becomes evident after drawing the standing wave pattern for this harmonic. Then, plug in 40.0 cm for length and calculate the wavelength.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
46. The diagrams below represent four different standing wave patterns in air columns of the same length. Which of the columns is/are vibrating at its/their fundamental frequency? Include all that apply.
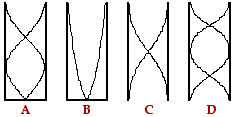
|
Answer: CD
The fundamental frequency is the lowest possible frequency for that instrument, and thus the longest possible wavelength. For open tubes, there would be anti-nodes on each end and a node in the middle. For closed end tubes, there would be a node on the closed end, an anti-node on the open end, and nothing in the middle. Diagram C is the third harmonic for a closed end tube and diagram D is the second harmonic for an open-end tube.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
47. The diagrams above (Question #46) represent four different standing wave patterns in air columns of equal length. Which of the columns will produce the note having the highest pitch?
|
a. A
|
b. B
|
c. C
|
d. D
|
|
e. All column produce notes having the same pitch
|
|
Answer: D
Just look at the wave patterns and notice that the shortest wavelength is in diagram D and so it must have the highest frequency or pitch.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
48. An air column closed at one end filled with air resonates with a 200.-Hz tuning fork. The resonant length corresponding to the first harmonic is 42.5 cm. The speed of the sound must be ____.
|
a. 85.0 m/s
|
b. 170. m/s
|
c. 340 m/s
|
d. 470. m/s
|
e. 940. m/s
|
|
Answer: C
Draw the standing wave pattern for the first harmonic of a closed-end tube to assist with the length-wavelength relation. Then, L=0.425 m so w=1.70 m. Since f is given as 200. Hz, the speed can be calculated as f*w or 200. Hz*1.70 m. The speed of sound is 340. m/s.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
49.TRUE or FALSE:
A violinist plays a note whose fundamental frequency is 220 Hz. The third harmonic of that note is 800 Hz.
|
Answer: B
The frequency of the nth harmonic is n times the frequency of the first harmonic where n is an integer. Thus, f3 = 3*f1 = 3*220 Hz = 660 Hz.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
50. In order for two sound waves to produce audible beats, it is essential that the two waves have ____.
|
a. the same amplitude
|
b. the same frequency
|
|
c. the same number of overtones
|
d. slightly different amplitudes
|
|
e. slightly different frequencies
|
|
|
Answer: E
Beats occur whenever two sound sources emit sounds of slightly different frequencies. Perhaps you recall the demonstration in class with the two tuning forks of slightly different frequencies.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
51. TRUE or FALSE:
Two tuning forks with frequencies of 256 Hz and 258 Hz are sounded at the same time. Beats are observed; 2 beats will be heard in 2 s.
|
Answer: B
Beats occur whenever two sound sources emit sounds of slightly different frequencies. The beat frequency is just the difference in frequency of the two sources. In this case, the beat frequency would be 2.0 Hz, which means that 2 beats would be heard every 1 second or 4 beats every 2 seconds.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
52. A tuning fork of frequency 384 Hz is sounded at the same time as a guitar string. Beats are observed; exactly 30 beats are heard in 10.0 s. The frequency of the string in hertz is ____.
|
a. 38.4
|
b. 354 or 414
|
c. 369 or 399
|
d. 374 or 394
|
e. 381 or 387
|
|
Answer: E
Beats occur whenever two sound sources emit sounds of slightly different frequencies. The beat frequency is just the difference in frequency of the two sources. In this case, the beat frequency is given as 3.00 Hz, which means that the second source must have a frequency of either 3.00 Hz above or 3.00 Hz below the first source - either 381 Hz or 387 Hz.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
Part C: Problem-Solving and Computational Problems
53. Determine the decibel rating of the following intensities of sound.
- I = 1.0 x 10-5 W/m2
- I = 1.0 x 10-2 W/m2
- I = 6.1 x 10-6 W/m2
- I = 2.2 x 10-4 W/m2
- A sound which is 4 times more intense than the sound in part d.
- A sound which is 7 times more intense than the sound in part d.
- A sound which is 10 times more intense than the sound in part d
- A sound which is 100 times more intense than the sound in part d.
- The sound of an orchestra playing a movement pianissimo at 7.5 x 10-6 W/m2 (very softly)
- The sound of an orchestra playing a movement fortissimo at 2.5 x 10-4 W/m2 (very loudly)
|
Answers: See below
The equation which relates the intensity of a sound wave to its decibel level is:
dB = 10 * log( I / 1.0 x 10-12 W/m2)
where I = intensity of the sound in units of W/m2. Using this equation, parts a - d can be computed in straightforward fashion.
a. dB = 10 * log( 1 x 10-5 W/m2 / 1.0 x 10-12 W/m2) = 70. dB
b. dB = 10 * log( 1 x 10-2 W/m2 / 1.0 x 10-12 W/m2) = 100. dB
c. dB = 10 * log( 6.1 x 10-6 W/m2 / 1.0 x 10-12 W/m2) = 68 dB
d. dB = 10 * log( 2.2 x 10-4 W/m2 / 1.0 x 10-12 W/m2) = 83 dB
e. The intensity is 4 x (2.2 x 10-4 W/m2 ) or 8.8 x 10-4 W/m2 ; so the decibel rating is 89 dB.
f. The intensity is 7 x (2.2 x 10-4 W/m2 ) or 1.54 x 10-3 W/m2 ; so the decibel rating is 92 dB.
g. The intensity is 10 x (2.2 x 10-4 W/m2 ) or 2.2 x 10-3 W/m2 ; so the decibel rating is 93 dB.
h. The intensity is 100 x (2.2 x 10-4 W/m2 ) or 2.2 x 10-2 W/m2 ; so the decibel rating is 103 dB.
i. dB = 10 * log( 7.5 x 10-6 W/m2 / 1.0 x 10-12 W/m2) = 69 dB
j. dB = 10 * log( 2.5 x 10-4 W/m2 / 1.0 x 10-12 W/m2) = 84 dB
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
54. A machine produces a sound with an intensity of 2.9 x 10-3 W/m2. What would be the decibel rating if four of these machines occupy the same room?
|
Answer: 101 dB
Four of these machines would be four times as intense as one machine - that would be an intensity of 1.16 x 10-2 W/m2 . The decibel rating is
dB = 10 * log( 1.16 x 10-2 W/m2 / 1.00 x 10-12 W/m2) = 101 dB
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
55. The sound in the United Center during a Chicago Bulls basketball game in 1998 was seven times as intense as it is today. If the decibel rating today is 89 dB, then what was the intensity rating in 1998?
|
Answer: 5.56 x 10-3 W/m2
This problem involves finding the intensity level in the stadium today and then multiplying it by seven. The conversion from dB to intensity in W/m2 is done using the usual equation.
dB = 10 * log( I / 1 x 10-12 W/m2)
The decibel level is substituted into the equation and then each side is divided by 10.
89 dB = 10 * log( I / 1 x 10-12 W/m2)
8.9 = log( I / 1 x 10-12 W/m2)
Now to solve for I, take the invlog of each side of the equation.
invlog(8.9) = invlog( log( I / 1 x 10-12 W/m2) )
7.94 x 108 = I / 1 x 10-12 W/m2
Now multiply both sides of the equation by 1 x 10-12 W/m2 to solve for I.
7.94 x 10-4 W/m2 = I
Now multiply by 7 since the intensity was seven times greater.
I = 5.56 x 10-3 W/m2
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
56. A sound has an intensity of 8.0 x10-3 W/m2 at a distance of 2.0 m from its source. What is the intensity at a distance of ...
- ... 4.0 m from the source?
- ... 6.0 m from the source?
- ... 8.0 m from the source?
- ... 24.0 m from the source?
- ... 46.1 m from the source?
|
Answers: See below.
This problem tests your understanding of the inverse square law: the intensity of a sound varies inversely with the square of the distance from the source of the sound.
I = k • (1/R2)
a. As the distance is doubled (4 m is two times 2 m), the intensity level is reduced by a factor of 4. The new intensity is 8.0 x10-3 W/m2/ 4 = 2.0 x10-3 W/m2.
b. As the distance is tripled (6 m is three times 2 m), the intensity level is reduced by a factor of 9. The new intensity is 8.0 x10-3 W/m2/ 9 = 8.9 x10-4 W/m2.
c. As the distance is quadrupled (8 m is four times 2 m), the intensity level is reduced by a factor of 16. The new intensity is 8.0 x10-3 W/m2/ 16 = 5.0 x10-4 W/m2.
d. As the distance is increased by a factor of 12 (24 m is 12 times 2 m), the intensity level is reduced by a factor of 144. The new intensity is 8.0 x10-3 W/m2/ 144 = 1.4 x10-5 W/m2.
e. As the distance is increased by a factor of 23.05 (46.1 m is 23.05 times 2 m), the intensity level is reduced by a factor of 531. The new intensity is 8.0 x10-3 W/m2/ 531 = 1.5 x10-5 W/m2.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
57. Ben Stupid is sitting 2.0 m in front of the speakers on the stage at the Twisted Brother concert. The decibel rating of the sound heard there is 110 dB. What would be the decibel rating at a location of ...
- ... 4.0 m from the speaker?
- ... 6.0 m from the speaker?
- ... 20.0 m from the speaker?
|
Answer: See answers below.
This problem is similar to the last problem in that it tests your understanding of the inverse square law. There is however a slight twist. The decibel rating is given and since the decibel scale is logarithmic, we must first find the intensity level before we do the division. A decibel rating of 110 db is equivalent to an intensity level of 1011 times the threshold of hearing (1 x 10-12 W/m2). So the intensity level at 2.0 m from the speaker is 0.1 W/m2. Now the inverse square law is applied; the intensity of a sound varies inversely with the square of the distance from the source of the sound.
I = k • (1/R2)
a. As the distance is doubled (4 m is two times 2 m), the intensity level is reduced by a factor of 4. The new intensity is 0.1 W/m2/ 4 = 0.025 W/m2 or 2.5 x10-2 W/m2. This converts to a decibel rating of 104 dB.
b. As the distance is tripled (6 m is three times 2 m), the intensity level is reduced by a factor of 9. The new intensity is 0.1 W/m2/ 9 = 0.011 W/m2 or 1.1 x10-2 W/m2. This converts to a decibel rating of 100.5 dB.
c. As the distance is increased by a factor of 10 (20 m is 10 times 2 m), the intensity level is reduced by a factor of 100. The new intensity is 0.1 W/m2/ 100 = 0.0010 W/m2 or 1.0 x10-3 W/m2. This converts to a decibel rating of 90 dB.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
58. Use the Doppler equation for a moving source to calculate the observed frequency for a 250.-Hz source of sound if it is moving with a speed of ____ . (Assume that the speed of sound in air is 340. m/s.)
- 30. m/s towards the observer.
- 30. m/s away from the observer.
- 300. m/s towards the observer.
- 300. m/s away from the observer.
- 320. m/s towards the observer.
- 335 m/s towards the observer.
|
Answers: See below.
The Doppler equation for determining the observed frequency for a moving source is:
fobserved = vsound / (vsound ± vsource) •fsource
The + sign is used if the source moves away from the observer
The - sign is used if the source moves towards the observer.
If applied to this situation, vsound is 340 m/s and fsource is 250 Hz.
a. fobserved = (340. m/s)/(340. m/s - 30. m/s) • (250 Hz) = (340. m/s)/(310. m/s) • (250. Hz) = 274 Hz
b. fobserved = (340. m/s)/(340. m/s + 30. m/s) • (250 Hz) = (340. m/s)/(370. m/s) • (250. Hz) = 230. Hz
c. fobserved = (340. m/s)/(340. m/s - 300. m/s) • (250 Hz) = (340. m/s)/(40. m/s) • (250. Hz) = 2130 Hz (2125 Hz)
d. fobserved = (340. m/s)/(340. m/s + 300. m/s) • (250 Hz) = (340. m/s)/(640. m/s) • (250. Hz) = 133 Hz
e. fobserved = (340. m/s)/(340. m/s - 320. m/s) • (250 Hz) = (340. m/s)/(20. m/s) • (250. Hz) = 4250 Hz
f. fobserved = (340. m/s)/(340. m/s - 335 m/s) • (250 Hz) = (340. m/s)/(5 m/s) • (250. Hz) = 1.70 x 104 Hz
|
|
Useful Web Links
|
|
None Currently Available
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
59. Shirley Yackin is holding the phone cord in her hand. It is stretched to a length of 2.4 m and has a mass of 1.8 kg. If the tension in the phone cord is 2.5 N, then determine the speed of vibrations within the cord.
|
Answer: 1.8 m/s
The telephone cord acts as a guitar string. As such the speed of waves in the cord is given by the equation
v = SQRT(Ftens/ mu)
where Ftens is the tension in the cord in Newtons and mu is the linear density in kg/m. The tension is given and the mu value can be calculated:
mu = mass/length = (1.8 kg) / (2.4 m) = 0.75 kg/m
Now substitute mu and Ftens into the equation and solve for speed:
v = SQRT[(2.5 N) / (0.75 kg/m)] = SQRT(3.33) = 1.8 m/s (1.8257 ... m/s)
|
|
Useful Web Links
|
|
None Currently Available
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
60. (Referring to problem #59.) With what frequency must Shirley vibrate the cord up and down in order to produce the second harmonic within the cord?
|
Answer: 0.763 Hz
 If Shirley is producing the second harmonic, then there will be one full wavelength in the length of the cord. Since the length of the cord is 2.4 m, the wavelength is 2.4 m as well (see diagram at right). With the wavelength and speed (problem #59) known, the frequency can be calculated. (Note that the unrounded number from problem #59 is used i this calculation.) If Shirley is producing the second harmonic, then there will be one full wavelength in the length of the cord. Since the length of the cord is 2.4 m, the wavelength is 2.4 m as well (see diagram at right). With the wavelength and speed (problem #59) known, the frequency can be calculated. (Note that the unrounded number from problem #59 is used i this calculation.)
f = v / lambda = (1.8257 m/s) / (2.4 m) = 0.76 Hz (0.7607... Hz)
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
61. (Referring to problem 60.) If Shirley maintains this same frequency and wishes to produce the fourth harmonic, then she will have to alter the speed of the wave by changing the tension. Assuming the same mass density as in #59, and the same frequency as in #60, to what tension must the cord be pulled to produce the fourth harmonic?
|
Answer: 0.63 N
 In this case, Shirley is changing the medium. So she is producing the fourth harmonic in a different medium (different properties) using the same frequency as in #60. For the fourth harmonic, there are two full wavelengths inside the length of the cord (see diagram at right); so the length of the wave (wavelength) is one-half the length of the cord - 1.2 m. With frequency and wavelength known, the speed can be computed: In this case, Shirley is changing the medium. So she is producing the fourth harmonic in a different medium (different properties) using the same frequency as in #60. For the fourth harmonic, there are two full wavelengths inside the length of the cord (see diagram at right); so the length of the wave (wavelength) is one-half the length of the cord - 1.2 m. With frequency and wavelength known, the speed can be computed:
v = f • lambda = (0.7607 Hz) • (1.2 m) = 0.91287... m/s.
Now with speed and mu known, the tension can be calculated from the equation:
v = SQRT(Ftens/ mu)
First, perform algebra to manipulate the equation into a form with Ftens by itself. This is done by squaring both sides of the equation and multiplying by mu.
v2 = Ftens/ mu
mu • v2 = Ftens
Now substitute and solve:
Ftens = (0.75 kg/m) • ( 0.91287... m/s)2 = 0.63 N (0.6250 N)
|
|
Useful Web Links
|
|
None Currently Available
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
62. A guitar string has a mass of 32.4 g and a length of 1.12 m. The string is pulled to a tension of 621 N. Determine the speed at which vibrations move within the string.
|
Answer: 147 m/s
This problem is very similar to question #59. The speed of waves in the guitar string is given by the equation
v = SQRT(Ftens/ mu)
where Ftens is the tension in the string in Newtons and mu is the linear density in kg/m. The tension is given and the mu value can be calculated (one will have to be careful of units):
mu = mass/length = (0.0324 kg) / (1.12 m) = 0.028928... kg/m
Now substitute mu and Ftens into the equation and solve for speed:
v = SQRT [ (621 N)/(0.028928... kg/m) ] = SQRT(21467) = 147 m/s (146.515... m/s)
|
|
Useful Web Links
|
|
None Currently Available
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
63. (Referring to problem #62.) Stan Dingwaives is playing this guitar. If Stan leaves the string "open" and uses its full length to produce the first harmonic, then what frequency will Stan be playing?
|
 Answer: 65.4 Hz Answer: 65.4 Hz
For the first harmonic, there is only one-half of a wave inside of the length of the string. So the length of the wave is two times longer than the length of the string (see diagram at right). Thus, the wavelength is 2.24 m. Now with speed and wavelength known, the frequency can be calculated.
f = v /lambda = (146.515... m/s) / (2.24 m) = 65.4 Hz (65.4085... Hz)
|
|
Useful Web Links
|
|
None Currently Available
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
64. (Referring to problem #62 and #63.) If Stan wishes to increase the frequency by a factor of 1.2599, then how far (in cm) from the end of the string must he "close" the string (i.e., where must he press his finger down to change the length and produce the desired frequency)? Use the same mass density and speed as in problem #62.
|
Answer: 0.23 m
For the same speed (same properties of the medium), frequency and wavelength are inversely related. Increasing the frequency by a factor of 1.2599 will be the result of decreasing the wavelength by the same factor. So the new wavelength will be
lambda = (2.24 m) / 1.2599 = 1.78 m
Since the wavelength is twice the effective length of the string, the string must have an effective length of 0.89 m or 89 cm. So, Stan must place his finger a distance of 0.23 m or 23 cm (1.12 m - 0.89 m) from the end of the string.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
65. A guitar string has a fundamental frequency of 262 Hz. Determine the frequency of the ...
- ... second harmonic.
- ... third harmonic.
- ... fifth harmonic.
- ... eighth harmonic.
|
Answers:
The frequencies of the various harmonics of an instrument are whole number rations of the fundamental frequency. The frequency of the second harmonic is two times the fundamental frequency; the frequency of the third harmonic is three times the fundamental frequency and so on. The frequencies of the harmonics can be found utilizing the formula
fn = n * f1
a. f2 = 2 * f1 = 2 * 262 Hz = 524 Hz
b. f3 = 3 * f1 = 3 * 262 Hz = 786 Hz
c. f5 = 5 * f1 = 5 * 262 Hz = 1310 Hz
d. f8 =8 * f1 = 8 * 262 Hz = 2.10x 103 Hz
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
66. Determine the speed of sound through air if the temperature is ...
- ... 0 degrees Celsius.
- ... 12 degrees Celsius.
- ... 25 degrees Celsius.
- ... 40 degrees Celsius.
|
Answers:
There are numerous equations for computing the speed of sound through air based on the temperature of air. A common equation found in books is
v = 331 m/s * SQRT (1 + T/273)
where T is the Celsius temperature. The following answers were found using this equation.
a. v = 331 m/s * SQRT (1 + 0/273) = 331 m/s
b. v = 331 m/s * SQRT (1 + 12/273) = 338 m/s
c. v = 331 m/s * SQRT (1 + 25/273) = 346 m/s
d. v = 331 m/s * SQRT (1 + 40/273) = 354 m/s
An alternative equation which is comonly used is v = 331 m/s + (.60 m/s/C)*T where T is the temperature is degrees celsius. Using this equation yields nearly the same same speed values - 331 m/s, 338 m/s, 346 m/s, and 355 m/s repsectively.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
67. A wind chime is an open-end air column. Determine the fundamental frequencies of a 62.5-cm chime when the temperature is ... .
- ... 12 degrees on a cold autumn evening.
- ... 25 degrees on a summer evening.
- ... 40 degrees during a hot summer day.
|
Answers:
 The frequency of the sound produced by a wind chime is related to the speed of air in the wind chime and the wavelength of the standing wave pattern of the resonating air column. The speed of the wave in air depends on the properties of air (temperature); these values were just computed in problem #66. The wavelength (lambda) of the resonating air column can be determined using a good diagram accompanied by the length of the air column. As depicted in the diagram at the right, the wavelength of the wave for the fundamental frequency is two times the length of the open-end air column. So in each of these cases, the wavelength is 2*62.5 cm = 125 cm = 1.25 m. With speed and wavelength known, the frequency values can be computed. The frequency of the sound produced by a wind chime is related to the speed of air in the wind chime and the wavelength of the standing wave pattern of the resonating air column. The speed of the wave in air depends on the properties of air (temperature); these values were just computed in problem #66. The wavelength (lambda) of the resonating air column can be determined using a good diagram accompanied by the length of the air column. As depicted in the diagram at the right, the wavelength of the wave for the fundamental frequency is two times the length of the open-end air column. So in each of these cases, the wavelength is 2*62.5 cm = 125 cm = 1.25 m. With speed and wavelength known, the frequency values can be computed.
a. f1 = v / lambda = (338 m/s) / (1.25 m) = 271 Hz
b. f1 = v / lambda = (346 m/s) / (1.25 m) = 277 Hz
c. f1 = v / lambda = (354 m/s) / (1.25 m) = 284 Hz
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
68. An organ pipe has a length of 2.45 m and is open at both ends. Determine the fundamental frequency of the pipe if the temperature in the room is 25 degrees Celsius.
|
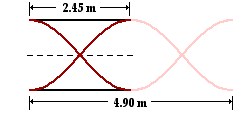 Answer: 70.6 Hz Answer: 70.6 Hz
For an open-end air column, the wavelength of the fundamental's standing wave pattern is two times the length of the air column; this relationship is depicted in the diagram at the right. So the wavelength of the wave is 4.90 m. The speed of the sound wave in air is dependent upon temperature. This speed was calculated in problem #66; it is 346 m/s. The frequency of the fundamental can now be calculated:
f1 = v / lambda
f1 = (346 m/s) / (4.90 m) = 70.6 Hz
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
69. (Referring to problem #68.) Determine the fundamental frequency of the pipe if it is closed at one end.
|
Answer: 35.3 Hz
The easy way to solve this problem is to recognize that by changing an open end to a closed end has the effect of lengthening the wave by a factor of two. If the wavelength is twice as large, then the frequency is twice as small. Thus, divide the original answer of 70.6 Hz (question #68) by 2.
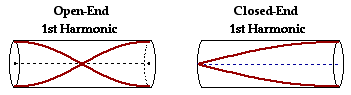
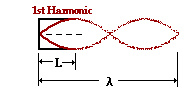
Alternatively, one could repeat the entire process of re-computing the wavelength from a diagram of the standing wave of the fundamental in a closed-end air column. For the fundamental, the wavelength is four times the length of the air column. In this case, the wavelength would be 9.80 m. Now divide the speed of the sound wave (346 m/s) by the wavelength value to obtain the frequency.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
70. The auditory canal of the outer ear acts as a closed end resonator which has a natural frequency of around 3500 Hz. This canal serves to amplify sounds with frequencies around this value, thus making us more sensitive to such frequencies. If the speed of waves inside the canal is 350 m/s, then what is the estimated length of the canal?
|
Answer: 2.5 cm
For closed end resonators, the standing wave patterns of the natural frequencies are characterized by a node at the closed end and an antinode at the open end. For the first harmonic (and it must be assumed that the 3500 Hz corresponds to the first harmonic), the wavelength is four times the length of the air column. The strategy in this problem involves determining the wavelength (lambda) from the speed and the frequency and then determining the length from the wavelength-length relationship.
lambda = v / f = (350 m/s) / (3500 Hz) = 0.1 m
L = 0.25 * lambda = 0.25 * (0.1 m) = 0.025 m = 2.5 cm
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
71. Determine the frequency of the lowest three harmonics at which a closed-end air column would sound out at 25 degrees Celsius if its length is 135 cm.
|
Answer: 64.0 Hz, 192 Hz, 320 Hz
The fundamental frequency of a closed-end air column is characterized by a standing wave pattern in which there is a node at the closed end and an antinode at the open end. There is one-fourth of a wavelength present within the length of the tube; thus, the wavelength is four times the length. In the case of this air column, the wavelength of the first harmonic is
lambda1 = 4*135 cm = 540 cm = 5.40 m
The speed of sound waves in air at 25 degree Celsius was computed in problem #66 to be 346 m/s. The frequency of the first harmonic can now be calculated from the speed and the wavelength.
f1 = v / lambda1 = (346 m/s) / (5.40 m) = 64.0 Hz
The next two lowest frequencies are the third and the fifth harmonics. (Recall the closed-end air columns do not have even-numbered harmonics.) The frequencies of these harmonics are multiples of the first harmonic frequency.
f3 = 3 * f1 = 3 * 64.0 Hz = 192 Hz
f5 = 5 * f1 = 5 * 64.0 Hz = 320 Hz
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
72. Suppose that a sound is produced in a helium-filled air column rather than an air-filled air column. By what factor will this change in medium alter the frequency of the sound. (GIVEN: vair = 331 m/s; vHe = 970 m/s)
|
Answer: 2.93
The frequency of a resonating air column is dependent upon the speed of sound in that air column; the relationship is a direct relationship. If the air is replaced by another gas that transmits sound waves with a different speed, then the frequency will be increased by the same factor by which the speed is increased. In this problem, the speed of sound is increased by a factor of
Factor = (970 m/s) / (331 m/s) = 2.93
Thus, the frequency is increased by a factor of 2.93.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
73. An organ pipe is used to produce the lowest note audible to the human ear - 20.-Hz. If the temperature is 25 °C, then how long is the organ pipe? (First decide whether it will produce this low note as a closed- or as an open-end air column.)
|
Answer: 4.3 m
Harmonics produced by closed-end air columns are characterized by longer wavelengths than the harmonics of open-end air columns of the same length. Thus, a closed-end air column produces lower frequencies. For this reason, we'll assume that the organ pipe in this problem is a closed-end air column. (Note, your answer will be two times larger if you assumed this to be an open-end air column.)
At a temperature of 25°C, sound waves travel at 346 m/s (see problem #66). The frequency and speed can be used to determine the wavelength (lambda):
lambda = v / f = (346 m/s) / (20. Hz) = 17.3 m
The wavelength of the first harmonic of a closed-end air column is four times the length of the column; so the length of the column is one-fourth the wavelength.
L = 0.25 * 17.3 m = 4.3 m
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
74. Determine the length of an open-end air column which would produce a 262 Hz frequency on a balmy day when the temperature is 12 degrees.
|
Answer: 64.5 cm
The speed of sound waves at 12 °C is 338 m/s (see problem #66). The wavelength (lambda) of a 262 Hz sound at this temperature is
lambda = v / f = (338 m/s) / (262 Hz) = 1.29 m
For an open-end air column, the wavelength of the first harmonic is two times the length of the air column. So the length is one-half the wavelength:
L = 0.5 * 1.29 m = 0.645 m = 64.5 cm
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
75. A 440.-Hz tuning fork is held above the open end of a water-filled pop bottle and resonance is heard. The length of the pop bottle (bottom to top) is 28.2 cm. If the speed of sound is 345 m/s, then to what height is the pop bottle filled with water?
|
Answer: 19.6 cm
The wavelength (lambda) of a 440 Hz sound can be determine from the wave equation (v = f*lambda)
lambda = v / f = (345 m/s) / (440. Hz) = 0.784 m
For a closed-end air column, the wavelength of the first harmonic is four times the length of the air column. So the length is one-fourth the wavelength:
L = 0.25 * 0.784 m = 0.196 m = 19.6 cm
If the pop bottle is 28.2 cm tall, then it should be filled with 8.6 cm of water in order for there to remain 19.6 cm of air.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 |#67 | #68 | #69 | #70 | #71 | #72 | #73 | #74 | #75 ]
Navigate to:
Review Session Home - Topic Listing
Sound Waves and Music - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-#9 || #10-#52 || #53-#64 || #65-#75
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Sound and Music
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 5 of the series includes topics on Sound Waves and Music.
Visit: MOP the App Home || MOP the App - Part 5