Waves, Sound and Light: Wave Basics
Calculator Pad, Version 2
You are viewing the Legacy Version of The Calculator Pad. We have recently revised and improved The Calculator Pad.
Version 2 is now LIVE! We have more than tripled the number of problems, broken each unit into several smaller, single-topic problem sets, and utilized a random number generator to provide numerical information for each problem. Student answers are automatically evaluated and feedback is instant. And we've maintained the same commitment to providing help via links to existing resources. While the FREE version does all the above, teachers with a Task Tracker subscription can take things a step further. They can modify our pre-made problem sets, write their own problems with our easy-to-use Problem Builder, and use the Calculator Pad to design their own program that expresses their emphasis on the use of mathematics in Physics.
Return to the
Main Page to link into Version 2. Learn more
About Version 2. Or visit the
Store to make a Task Tracker purchase.
Wave Basics: Problem Set
Problem 1:
Jerome and Claire are doing the Period of a Pendulum Lab. They observe that a pendulum makes exactly 10 complete back and forth cycles of motion in 21.8 seconds. Determine the period of the pendulum.
Problem 2:
Strong winds can apply a significant enough force to tall skyscrapers to set them into a back-and-forth motion. The amplitudes of these motions are greater at the higher floors and barely observable for the lower floors. It is said that one can even observe the vibrational motion of the Sears Tower in Chicago on a windy day. As the Sears Tower vibrates back and forth, it makes about 8.6 vibrations in 60 seconds. Determine the frequency and the period of vibration of the Sears Tower.
Problem 3:
The spin rate of a CD-ROM varies according to the location on the disc from where data is being accessed. When accessing data from the inner circles of the disc, the CD can spin at a rate as high as 400 revolutions per minute. Determine the frequency (in Hertz) and the period (in seconds) of the spinning CD.
Problem 4:
Like all planets, the planet Venus orbits the Sun in periodic motion and simultaneously spins about its axis. Just as on Earth, the time to make one complete orbit (i.e., the period of orbit) is what defines a year. And the time to make one complete revolution about its axis (i.e., the period of rotation) is what defines a day. The period of orbit for the Earth is 365.25 days and the period of rotation is 24 hours (1.00 day). But when these same values for Venus are expressed relative to Earth, it is found that Venus has a period of orbit of 225 days and a period of rotation of 243 days. So for Venus inhabitants, a day would last longer than a year! Determine the frequency of orbit and the frequency of rotation (in Hertz) on Venus.
Problem 5:
Extreme waves along ocean waters, sometimes referred to as freak waves or rogue waves, are a focus of much research and study among scientists. Several merchant ships reports rogue waves which are estimated to be 25 meters high and 26 meters long. Assuming that these waves travel at speeds of 6.5 m/s, determine the frequency and the period of these waves.
Problem 6:
Tsunamis are much different than rogue waves. While rogue waves and other waves are generated by winds, tsunamis originate from geological events such as movements of tectonic plates. Tsunamis tend to travel very fast. A tsunami generated off the coast of Chile in 1990 is estimated to have traveled approximately 6200 miles to Hawaii in 15 hours. Determine the speed in mi/hr and m/s. (Given: 1.0 m/s = 2.24 mi/hr)
Problem 7:
A geological disturbance in California produces seismic waves which are detected in Phoenix, approximately 990 km from the epicenter. If the waves travel 6.3 km/s, determine the time delay between the disturbance and the detection.
Problem 8:
Microbats use echolocation to navigate and hunt. They emit pulses of high frequency sound waves which reflect off obstacles and objects in their surroundings. By detecting the time delay between the emitted pulse and the return of the reflected pulse, a bat can determine the location of the object. Determine the time delay between the sending of a pulse and the return of its reflection from an object located 12.5 m away. Approximate the speed of the sound waves as 345 m/s.
Problem 9:
Logan, Cassie and Abbey are doing the Pulse Speed Lab. Logan and Cassie stand 6.8 m apart and stretch a zinc-coiled snakey between them. Logan introduces a pulse into the snakey at his end. Using a stopwatch, Abbey measures that it takes 15.1 seconds for the pulse to travel to Cassie's end and back two times. They then repeat the experiment with a copper-coiled snakey stretched the same distance and find that pulses travel back and forth two times in 16.9 seconds.
a. Determine the speed of the pulse in the zinc-coiled snakey.
b. Determine the speed of the pulse in the copper-coiled snakey.
Problem 10:
Sachi is rock'n to her favorite radio station - 102.3 FM. The station broadcasts radio signals with a frequency of 1.023 x 108 Hz. The radio wave signal travel through the air at a speed of 2.997 x 108 m/s. Determine the wavelength of these radio waves.
Problem 11:
A transverse wave is observed to be moving along a lengthy rope. Adjacent crests are positioned 2.4 m apart. Exactly six crests are observed to move past a given point along the medium in 9.1 seconds. Determine the wavelength, frequency and speed of these waves.
Problem 12:
A marine weather station detects waves which are 9.28 meters long and 1.65 meters high and travel a distance of 50.0 meters in 21.8 seconds. Determine the speed and the frequency of these waves.
Problem 13:
Humpback whales are known to produce a collection of elaborate and repeating sounds with frequencies ranging from 20 Hz to 10 kHz. The sound waves travel through water at speeds of approximately 1400 m/s. Determine the wavelengths of the waves at the lower and the upper end of this frequency range.
Problem 14:
A wave is traveling in a rope. The diagram below represents a snapshot of the rope at a particular instant in time.
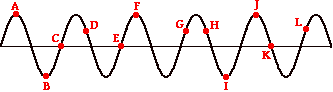
Determine the number of wavelengths which is equal to the horizontal distance between points …
a. … C and E on the rope.
b. … C and K on the rope.
c. … A and J on the rope.
d. … B and F on the rope.
e. … D and H on the rope.
f. … E and I on the rope.
Problem 15:
Ryan and Carson attended their church's youth retreat at Camp Paradise this past fall. On Saturday afternoon they took a walk out to the harbor and watched incoming waves from Lake Michigan rock the boating piers up and down. Ryan and Carson observed that the piers made a complete up and down vibration cycle in 6.6 seconds. The piers were positioned a distance of 24 meters apart. When one pier was at a high position, the neighboring pier was at a low position and there was exactly one wave crest between them. Determine the wavelength, frequency and speed of the waves.
Problem 16:
Nick and Kara were lounging on rafts in the shallow waters of the beach at Lake Bluebird. They were spaced 1.8 meters apart. A motor boat zoomed past creating ripples which traveled towards Nick and Kara. Nick and Kara's rafts began to bob up and down as the ripples passed by them, making exactly 4 up and down cycles in 8.4 seconds. When Nick's raft was at a high point, Kara's raft was at a low point and there were no crests between their boats. Determine the wavelength, frequency and speed of the ripples Assume that the ripples traveled in a direction parallel to the imaginary line connecting the two rafts.
Problem 17:
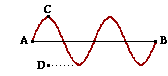 A wave with a frequency of 12.3 Hz is traveling from left to right across a rope as shown in the diagram at the right Positions A and B in the diagram are separated by a horizontal distance of 42.8 cm. Positions C and D in the diagram are separated by a vertical distance of 12.4 cm. Determine the amplitude, wavelength, period and speed of this wave.
A wave with a frequency of 12.3 Hz is traveling from left to right across a rope as shown in the diagram at the right Positions A and B in the diagram are separated by a horizontal distance of 42.8 cm. Positions C and D in the diagram are separated by a vertical distance of 12.4 cm. Determine the amplitude, wavelength, period and speed of this wave.
Problem 18:
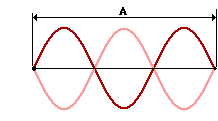 A rope is held tightly and shook until the standing wave pattern shown in the diagram at the right is established within the rope. The distance A in the diagram is 3.27 meters. The speed at which waves move along the rope is 2.62 m/s.
A rope is held tightly and shook until the standing wave pattern shown in the diagram at the right is established within the rope. The distance A in the diagram is 3.27 meters. The speed at which waves move along the rope is 2.62 m/s.
a. Determine the frequency of the waves creating the standing wave pattern.
b. Determine the number of vibrational cycles which would be measured in 20.0 seconds.
Problem 19:
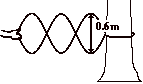 Anna Litical ties a rope to a tree, stands 7.2 m away, and vibrates the rope up and down with 28 complete cycles in 5.0 seconds. The resulting standing wave pattern is shown in the diagram at the right. Use this information and the diagram to determine the amplitude, wavelength, frequency and speed.
Anna Litical ties a rope to a tree, stands 7.2 m away, and vibrates the rope up and down with 28 complete cycles in 5.0 seconds. The resulting standing wave pattern is shown in the diagram at the right. Use this information and the diagram to determine the amplitude, wavelength, frequency and speed.
Problem 20:
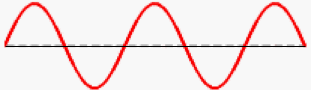
In the Standing Wave Lab, lab partners Chloe and Paige adjust the frequency of a mechanical oscillator in order to vibrate a 1.38 m length of elastic cord at one of its harmonic frequencies. The cord vibrates with the pattern shown below when the frequency is set to 79.4 Hz. Determine the speed of the waves in the elastic cord.
Problem 21:
In a physics demonstration, Mr. H establishes a standing wave pattern in a snakey by vibrating it up and down with 32 vibrations in 10 seconds. Gerald is holding the opposite end of the snakey and is standing 6.2 m from Mr. H's end. There are four equal length sections in the snakey, each occupied by an antinode. Determine the frequency, wavelength and speed of the wave.
Problem 22:
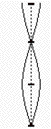 Gillian drives down Lake Avenue and observes an odd vibrational pattern of her car antenna. She observes it vibrating back and forth in the manner shown at the right. There is an antinode at its free end and a node at the location where the antenna mounts to the car. Vibrations travel through the 86 cm tall antenna at 5.0 x 103 m/s. Determine the frequency of vibrations of the antenna.
Gillian drives down Lake Avenue and observes an odd vibrational pattern of her car antenna. She observes it vibrating back and forth in the manner shown at the right. There is an antinode at its free end and a node at the location where the antenna mounts to the car. Vibrations travel through the 86 cm tall antenna at 5.0 x 103 m/s. Determine the frequency of vibrations of the antenna.
Problem 23:
Anna Litical and Stan Dingwaives are holding an elastic cord between them. Using a 1.6 meter long rope, they create a wave which travels at 2.4 m/s and has a frequency of 1.5 Hz. What would be the new wavelength and speed if they double the frequency of vibration of the cord?
Problem 24:
A standing wave pattern is established in a 246-cm long rope. A snapshot of the rope at a given moment in time is shown in the diagram below. Vibrations travel within the rope at speeds of 22.7 m/s. Determine the frequency of vibration of the rope.

Problem 25:
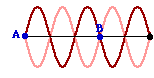 A standing wave is established in a snakey as shown in the diagram at the right. The distance from point A to point B is known to be 4.69 meters. When not being vibrated as a standing wave, a single pulse introduced into the medium at point A will travel to the opposite end and back in 2.70 seconds. Determine the vibrational frequency of the wave pattern.
A standing wave is established in a snakey as shown in the diagram at the right. The distance from point A to point B is known to be 4.69 meters. When not being vibrated as a standing wave, a single pulse introduced into the medium at point A will travel to the opposite end and back in 2.70 seconds. Determine the vibrational frequency of the wave pattern.
Problem 26:
A 144 cm long rope undergoes exactly 64 complete vibrational cycles in 17.6 seconds when vibrating in the third harmonic (in three equal-length sections). Determine the speed of the waves in the rope.
Problem 27:
In a physics lab, a rope is observed to make 240 complete vibrational cycles in 15 seconds. The length of the rope is 2.8 meters and the measurements are made for the 6th harmonic (with six equal length sections). Determine the speed of the waves in the rope.
Problem 28:
Winston and Michal hold opposite ends of a stretched rope. Winston introduces a 68-cm tall upward-displaced pulse on his end while Michal simultaneously introduces a 42-cm tall upward-displaced pulse on his end. The two pulses meet in the middle of the rope.
a. What is the resultant displacement of the rope when they completely overlap?
b. What would be the resultant displacement of the rope if Michal's pulse was displaced downward?
Problem 29:
During a classroom demonstration, Mr. H uses a wave machine donated to the school by Bell Telephone Company. The wave machine consists of two 1-meter length sections of 50 steel rods. The steel rods are connected to each other so that when the first rod is disturbed from a rest position, the disturbance travels along the medium from rod to rod. One of the sections consists of longer steel rods; disturbances move at 20 cm/s in this section. The other section consists of shorter steel rods; disturbances move at 80 cm/s in this section. Mr. H connects the two sections together so that pulses can cross the boundary from one section to the other. He introduces a pulse with a length of 10 cm into the slower section. Determine the length of this pulse when it crosses the boundary into the faster section.
Return to Overview
View Audio Guided Solution for Problem:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29