Circular Motion and Gravitation Review
Navigate to:
Review Session Home - Topic Listing
Circular Motion and Gravitation - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-14 || #15-28 || #29-40
Part E: Problem-Solving
29. A roller coaster car loaded with passengers, has a mass of 500 kg; the radius of curvature of the track at the bottom point of a dip is 12 m. The vehicle has a speed of 18 m/s at this point.
- In the space below, draw a free-body diagram for the car (label forces according to type).
- Calculate the acceleration and the net force acting upon the car. PSYW
- Calculate the force exerted on the vehicle by the track? PSYW
|
Answers:
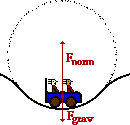 The free-body diagram (part a) is shown at the right. The free-body diagram (part a) is shown at the right.
The acceleration of the car can be computed as follows:
a = v2/R = (18.0 m/s)2/(12.0 m) = 27.0 m/s2 (part b)
The net force can be found in the usual manner:
Fnet = m•a = (500. kg)•(27.0 m/s2) = 13500 N (part b)
Since the center of the circle (see diagram) is above the riders, then both the net force and the acceleration vectors have an upward direction. The force of gravity is downwards, so the net force is equal to the upward force minus the downward force:
Fnet = Fnorm - Fgrav
where Fgrav = m • g = (500. kg) • (9.8 m/s/s) = 4900 N
Thus,
Fnorm = Fnet + Fgrav = 13500 N + 4900 N = 18400 N (part c)
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
30. What is the acceleration of a piece of dust on an old-fashioned record album, 15 cm from the center, if the record is spinning at 33.3 rpm?
|
Answer: 1.82 m/s/s
To find acceleration, the speed and the radius must be known. The radius is given; the speed can be computed as distance per time. The dust moves a distance equivalent to 33.3 circumferences in 60 seconds. So
v = 33.3 • 2 • pi • (0.15 m) / (60 s) = 0.523 m/s.
The acceleration can now be computed using the centripetal acceleration equation:
a = v2/R = (0.523 m/s)2 / (0.15 m) = 1.82 m/s/s
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
31. What is the tension in a 0.500 meter rope which carries a 2.50 kg bucket of water in a vertical circle with a velocity of 3.00 m/s when the bucket is at the bottom of its swing?
|
Answer: 69.5 N
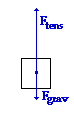 Begin with a free-body diagram for the bucket at the bottom of its string. Since the bucket is at the bottom of the circle, the net force is upwards (inwards). Notice that the tension force must be greater than the force of gravity in order to have a net upwards (inwards) force. Also note that while Ftens is directed in the direction of the net force, Fgrav is in the opposite direction. Thus, the equation can be written: Begin with a free-body diagram for the bucket at the bottom of its string. Since the bucket is at the bottom of the circle, the net force is upwards (inwards). Notice that the tension force must be greater than the force of gravity in order to have a net upwards (inwards) force. Also note that while Ftens is directed in the direction of the net force, Fgrav is in the opposite direction. Thus, the equation can be written:
Fnet = Ftens - Fgrav
This equation can be rearranged to solve for tension; the expressions for Fgrav (m•g) and Fnet (m•v2/R) can be substituted into it:
Ftens = Fnet + Fgrav = m•v2/R + m•g = (2.50 kg)•(3.00 m/s)2/(0.500 m) + (2.50 kg)•(9.8 m/s2)
Ftens = 69.5 N
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
32. A 53.5-kg rider on a roller coaster car is moving 10.3 m/s at the top of a loop which has a radius of curvature of 7.29 m. Determine the normal force experienced by the rider.
|
Answer: 254 N
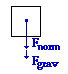 At the top of the loop, both the gravitational and the normal force are directed inwards (as shown in the free-body diagram at the right). Thus, the Fnet equation can be written as: At the top of the loop, both the gravitational and the normal force are directed inwards (as shown in the free-body diagram at the right). Thus, the Fnet equation can be written as:
Fnet = Fgrav + Fnorm
This equation can be rearranged and the expressions for Fgrav (m•g) and Fnet (m•v2/R) can be substituted into it:
Fnorm = Fnet - Fgrav = m • v2 / R - m • g
Fnorm = (53.5 kg) • (10.3 m/s)2 / (7.29 m) - (53.5 kg) • (9.8 m/s2)
Fnorm = 254 N
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
33. Determine the minimum coefficient of friction required to keep a 920.-kg car on a turn with a radius of 26.8 m. The car is traveling 29.9 m/s and the roadway is level.
|
Answer: 3.40
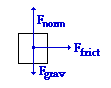 As usual, begin with a free-body diagram. The gravity force is balanced by (and equal to) the normal force and the force of friction is the net force. The solution then begins by equating m • a to Ffrict and carrying out the customary substitutions and algebra steps (using the fact that a = v2 / R and Ffrict = µ • Fnorm and Fgrav = m • g). As usual, begin with a free-body diagram. The gravity force is balanced by (and equal to) the normal force and the force of friction is the net force. The solution then begins by equating m • a to Ffrict and carrying out the customary substitutions and algebra steps (using the fact that a = v2 / R and Ffrict = µ • Fnorm and Fgrav = m • g).
m•a = Ffrict
m • v2/R = µ • Fnorm
m • v2/R = µ • m • g
The mass now cancels and the equation can be rearranged to solve for mu:
µ = v2/(g• R) = (29.9 m/s)2 / [ (9.8 m/s2) • (26.8 m)] = 3.40
(This is not a likely mu value and as such the car does not have much of a chance negotiating the turn at this speed.)
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
34. With what speed (in mi/hr) must you drive your car across the crest of a hill of radius 37.1-m in order to feel weightless (1.00 m/s = 2.24 mi/hr)?
|
Answer: 42.8 mi/hr (19.1 m/s)
The feeling of weightlessness is experienced when a person is under the sole influence of gravity. So the free-body diagram for such a person would reveal only one force - gravity, pointing straight down. In such a case, the seat does not push upward upon the person. The car has passed over the crest of the hill at such a high speed that it is momentarily raised off the roadway and is unable to support the weight of its passengers. The force of gravity is the net force and the following equation can be written:
m • a = m • g
The mass can be canceled from both sides of the equation (sigh!) and the expression for acceleration can be substituted into the equation, yielding:
v2/R = g
Rearrangement and substitution yields the solution:
v = SQRT(g • R) = [(9.8 m/s2) • (37.1 m)] = SQRT[364 m2/s2] = 19.1 m/s
This value for speed can be converted to mi/hr using the equivalency: 2.24 mi/hr = 1m/s; the car is traveling with a speed of 42.8 mi/hr.
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
35. What is the reading of a bathroom scale when a man of mass 72 kg stands on it while riding in an elevator accelerating upwards at 5.4 m/s2?
|
Answer: 1.1 x 103 N
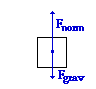 The scale reading is a measure of the amount of normal force acting upon the person. As is the usual case, begin with a free-body diagram (shown at the right). Since the acceleration is upwards, the upwards normal force (Fnorm) is greater than the downwards gravitational force (Fgrav). From the diagram, the Fnet equation can be written: The scale reading is a measure of the amount of normal force acting upon the person. As is the usual case, begin with a free-body diagram (shown at the right). Since the acceleration is upwards, the upwards normal force (Fnorm) is greater than the downwards gravitational force (Fgrav). From the diagram, the Fnet equation can be written:
Fnet = Fnorm - Fgrav
Algebraic rearrangement of this equation, combined with the understanding that Fnet = m•a and Fgrav = m•g yields the following solution:
Fnorm = Fnet + Fgrav = m•a + m•g = (72 kg) • (5.4 m/s2) + (72 kg) • (9.8 m/s2)
Fnorm = 1.1 x 103 N
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
36. An airplane pilot makes a vertical loop with a 56-2-m radius. Determine the normal force acting upon the pilot's 62.6-kg body at the top of the loop if his air speed is 64.1 m/s.
|
Answer: 3.96 x 103 N
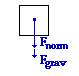 As usual, begin with a free-body diagram (shown at the right). From the diagram, the equation relating net force to the individual forces can be written: As usual, begin with a free-body diagram (shown at the right). From the diagram, the equation relating net force to the individual forces can be written:
Fnet = Fnorm + Fgrav
Since Fnet = m•a = m•v2/R and Fgrav = m•g, substitutions can be made and the equation can be rewritten:
m•v2/R = Fnorm + m•g
Rearranging to solve for Fnorm yields:
Fnorm = m•v2/R - m•g = (62.6 kg) • (64.1 m/s)2 / (56.2 m) - (62.6 kg) • (9.8 m/s2)
Fnorm = 3.96 x 103 N
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
37. Use the following information to help determine the acceleration of the planet Pluto about the sun.
Mass of Sun = 1.991 x 1030 kg
Sun-Pluto Distance = 5.91 x 1012 m
|
Answer: g = 6.56 • 10-6 m/s2
Pluto's acceleration is caused by the gravitational force of attraction to the sun. Thus, one way (there are a couple of ways) to calculate the a of Pluto is to determine the acceleration of gravity towards the sun at the location of Pluto's orbit. The equation, substitution (using textbook values) and solution are shown below:
g = G • Msun / R2 = (6.67 • 10-11 N•m2/kg2) • (1.991 • 1030 kg) / (4.50 • 1012 m)2
g = 6.56 • 10-6 m/s2
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
38. What is the period of rotation of Venus in earth years if it is a distance of 1.08 x 1011 meters from the sun? (The earth-sun distance is 1.5 x 1011 m.)
|
Answer: 0.61 yr
This question explores the R-T relationship. As such, Kepler's third law - that the T2/R3 ratio is the same for all the planets - must be utilized.
Tearth2/Rearth3 = TVenus2/RVenus3
(1 year)2/(1.5 x 1011)3 = TVenus2 /(1.08 x 1011 m)3
Rearranging this equation to solve for the period of the planet yields the equation:
TVenus2 = (1 year)2 • (1.08 x 1011 m)3 /(1.5 x 1011)3 = (1 year)2) • (0.72)3 = 0.373 year2
TVenus = SQRT(0.373 year2 ) = 0.61 years
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
39. What is the gravitational attraction between the proton and electron in an Hydrogen atom if they are 5.3 x 10-11 meters apart? (mproton = 1.67 x 10-27 kg; melectron = 9.11x10-31 kg)
|
Answer: 3.6•10-47 N
Use Newton's universal gravitation equation:
Fgrav = G • m1 • m2 /R2
Fgrav = (6.67•10-11 N•m2/kg2) • (1.67 x 10-27 kg) • (9.11x10-31 kg) /(5.3 x 10-11 m)2
Fgrav = 3.6•10-47 N
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
40. Use the following information to help determine the orbital velocity and orbital period of a satellite at a location of 15000 miles above the surface of the earth.
Mass of Earth = 5.98 x 1024 kg
Radius of Earth = 6.37 x 106 m
1609 m = 1.00 mi
|
Answers:
The first step is to find the separation distance from the center of the earth - this is R in most of the equations. The altitude of the satellite is 15000 mi or 2.41•107 m; this distance must be added to the radius of the earth to determine the separation distance. The radius of the earth is 6.38•106 m; the separation distance is 3.05•107 m. The orbital velocity can be computed using the orbital velocity equation:
v = SQRT(G•Mcentral/R) = SQRT[ (6.67•10-11 N•m2/kg2) • (5.98•1024 kg) / (3.05•107 m) ]
v = SQRT (1.31•107 m2/s2) = 3615 m/s
The orbital period can now be calculated using the v = 2•pi•R/T equation or the Kepler's second law equation [ T2/R3 = 4•pi2/(GMearth)]. Starting with the first equation, algebra yields:
T = (2•pi•R)/v = [2 • pi • (3.05•107 m) / (3615 m/s) ] = 5.30 • 104 s = 14.7 hr
|
[ #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
Navigate to:
Review Session Home - Topic Listing
Circular Motion and Gravitation - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-14 || #15-28 || #29-40
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Circular Motion and Gravitation
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 2 of the series includes topics in Circular Motion and Gravitation.
Visit: MOP the App Home || MOP the App - Part 2