Circular Motion and Gravitation Review
Navigate to:
Review Session Home - Topic Listing
Circular Motion and Gravitation - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-14 || #15-28 || #29-40
Part A: Multiple Choice
1. Which of the following statements are true of an object moving in a circle at a constant speed? Include all that apply.
- The object experiences a force which has a component directed parallel to the direction of motion.
- Inertia causes objects to move in a circle.
- There can be a force pushing outwards on the object as long as the net force in inwards.
- Because the speed is constant, the acceleration is zero.
- The acceleration and the net force vector are directed perpendicular to each other.
- If the net force acting upon the object is suddenly reduced to zero, then the object would suddenly depart from its circular path and travel tangent to the circle.
- The acceleration of the object is directed tangent to the circle.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
For Questions #2-#5, identify the type of force which causes the following bold-faced objects to travel along a circular path.
2. An eraser is tied to a string swung in a horizontal circle.
|
a. gravity
|
b. normal
|
c. tension
|
d. applied
|
|
e. friction
|
f. spring
|
g. electrical
|
h. magnetic
|
3. The moon orbits the earth.
|
a. gravity
|
b. normal
|
c. tension
|
d. applied
|
|
e. friction
|
f. spring
|
g. electrical
|
h. magnetic
|
4. A car makes a sharp right-hand turn along a level roadway.
|
a. gravity
|
b. normal
|
c. tension
|
d. applied
|
|
e. friction
|
f. spring
|
g. electrical
|
h. magnetic
|
5. A roller coaster car passes through a loop. Consider the car at the bottom of the loop.
|
a. gravity
|
b. normal
|
c. tension
|
d. applied
|
|
e. friction
|
f. spring
|
g. electrical
|
h. magnetic
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
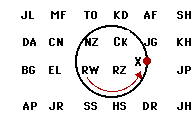 6. A physics teacher ties an eraser to the end of a string and then whirls it in a counter-clockwise circle. If the teacher lets go of the string, then the eraser hits a student (or several students) in the classroom. If the string is let go when the eraser is at point X on the diagram at the right, then which student(s) in the class will the eraser hit? Write the initials in this space: ________________
6. A physics teacher ties an eraser to the end of a string and then whirls it in a counter-clockwise circle. If the teacher lets go of the string, then the eraser hits a student (or several students) in the classroom. If the string is let go when the eraser is at point X on the diagram at the right, then which student(s) in the class will the eraser hit? Write the initials in this space: ________________
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
7. Which of the following statements are true about gravitational force? Identify all that apply.
- The gravitational force only acts between very, very massive objects.
- The gravitational force between an object and the earth is inversely related to the distance between the object's and the earth's center.
- The gravitational force can ALWAYS be accurately calculated by multiplying the object mass by the acceleration of gravity (m•g).
- The gravitational force acting upon an object is the same as the weight of the object.
- The gravitational force between two objects is independent of the mass of the smaller of the two objects.
- If object A gravitationally attracts object B with a force of X Newtons, then object B will also gravitationally attract object A with the same force of X Newtons.
- The doubling of the separation distance (measured from the center) between two objects will halve the gravitational force between the objects.
- It an object is placed two earth-radii above the surface of the earth, then the force of gravitational attraction between the object and the earth will be one-fourth the magnitude as on earth's surface.
- Orbiting astronauts do not experience a force of gravity; this explains why they feel weightless.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
8. Which of the following statements are true about the acceleration of gravity? Identify all that apply.
- The acceleration of gravity experienced by objects located near to (and far from) from the earth depends upon the mass of the object.
- The acceleration of gravity experienced by objects located near to (and far from) from the earth depends upon the mass of the Earth.
- The acceleration of gravity experienced by objects located near to (and far from) the earth is inversely related to the distance between the center of the object and the center of the earth.
- Increasing the mass of an object will increase the acceleration of gravity experienced by the object.
- Doubling the distance between an object and the earth's center will decrease the acceleration of gravity by a factor of four.
- The acceleration of an orbiting satellite is equal to the acceleration of gravity at that particular location.
- If the mass of the Earth were doubled (without an alteration in its radius), then the acceleration of gravity on its surface would be approximately 20 m/s2.
- If the mass of the Earth were doubled and the radius of the earth were doubled, then the two changes would offset each other and the acceleration of gravity on its surface would still be approximately 10 m/s2.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
9. Which of the following statements are true about satellites? Identify all that apply.
- Satellites are falling projectiles.
- All satellites follow circular paths.
- The orbital velocity required of a satellite is dependent upon the mass of the satellite; a more massive satellite would require a greater orbital speed.
- The orbital velocity of a satellite does not depend upon the mass of the planet around which it orbits.
- A high-altitude satellite will require a greater orbital speed than a low-altitude satellite.
- By definition, a geosynchronous satellite orbits the earth in a perfect circle, maintaining the same distance above the surface of the earth.
- Satellites travel faster along their orbital path when they are closest to the earth.
- The acceleration of a satellite varies inversely with its distance from the center of the earth. More distant satellites have smaller accelerations.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
10. Which of the following statements are true about the motion of planets about the sun? Identify all that apply.
- The force of gravity is the only force which acts upon the planets.
- Their trajectories are highly elliptical.
- The planets which are furthest from the sun have the greatest period.
- For any given planet, the speed is greatest when the planet is closest to the sun.
- The velocity vector is directed tangent to the elliptical path.
- The net force vector is at all times directed perpendicular to the velocity vector.
- To keep the planet from escaping the sun's gravitational field, the net force vector is greatest when the planet is furthest from the sun.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
Part B: Short Answer
11. Explain how something can be moving at a constant speed yet be accelerating at the same time.
12. How did Newton come up with the idea that the moon is actually "falling" toward the Earth.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
13. Distinguish between true- and apparent-weightlessness.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
14. Describe the apparent weight of a person in an elevator while upward, accelerating downward, and not accelerating.
Part C: Diagramming and Analysis
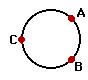 15. In the diagram at the right, draw vector arrows (straight lines with arrowheads) which indicate the following for an object which is moving in a clockwise circle.
15. In the diagram at the right, draw vector arrows (straight lines with arrowheads) which indicate the following for an object which is moving in a clockwise circle.
- the net force at point A.
- the acceleration at point B.
- the velocity at point C.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
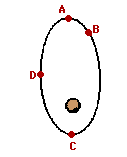 16. The diagram at the right shows a satellite orbiting the Earth in an elliptical path in a clockwise direction.
16. The diagram at the right shows a satellite orbiting the Earth in an elliptical path in a clockwise direction.
- Draw a vector representing the velocity of the object at position A.
- raw a vector representing the force on the object at position D.
- Draw a vector representing the acceleration of the object at position C.
- At which of the four positions is the satellite moving fastest?
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
17. A 1.20-kg bucket is held by a string and whirled in a vertical circle. The radius of the circle is 1.30 m. The speed of the bucket is 3.70 m/s at the top of the loop and 7.10 m/s at the bottom of the loop. On the diagrams below, construct a free-body diagram (label all forces according to type) for the bucket at both the top and the bottom of the loop. Fill in the blanks and clearly indicate the magnitude of the individual force values on your free-body diagram.
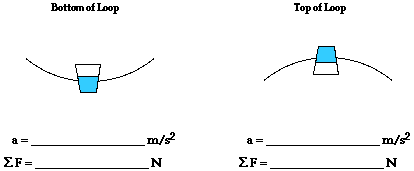
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
18. Construct a free-body diagram showing the direction and types of forces acting upon the car at the top and the bottom of a loop. Be sure to label the forces according to type.
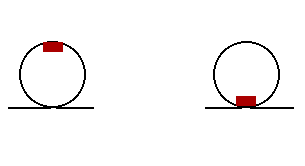
Anna experiences a downward acceleration of 24.0 m/s2 at the top of the loop and an upwards acceleration of 12.0 m/s2 at the bottom of the loop. Use Newton's second law to fill in all the blanks and to ultimately determine the normal force acting upon Anna's 800. kg roller coaster car. PSYW
|
Top
|
Bottom
|
|
Fnet = _______________
|
Fnet = _______________
|
|
Fgrav = _______________
|
Fgrav = _______________
|
|
Fnorm = _______________
|
Fnorm = _______________
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
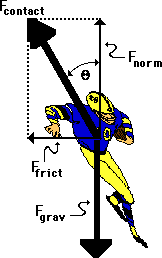
19. A fullback is running a sweep around the left side of the line. As he rounds the turn, he is momentarily moving in circular motion, sweeping out a quarter-circle with a radius of 4.17 meters. If the 83.5-kg fullback makes the turn with a speed of 5.21 m/s, then what is his acceleration, the net force, the angle of lean (measured to the vertical), and the total contact force with the ground? PSYW
a = ____________
Fnet = ____________
Fgrav = ____________
Fnorm = ____________
Ffrict = ____________
Fcontact = ____________
Angle of Lean = ____________
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
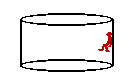 20. Pete Zaria is riding the Cliff Hanger at Great America. Pete enters a cylindrical barrel which makes 18.5 revolutions every minute. The diameter of the barrel is 6.92 m. Pete's mass is 64.7 kg. Construct a free-body diagram showing the forces acting upon Pete. Calculate the acceleration and net force acting upon Pete Zaria. Finally, determine the coefficient of friction between Pete and the walls that would be required to support Pete's weight. PSYW
20. Pete Zaria is riding the Cliff Hanger at Great America. Pete enters a cylindrical barrel which makes 18.5 revolutions every minute. The diameter of the barrel is 6.92 m. Pete's mass is 64.7 kg. Construct a free-body diagram showing the forces acting upon Pete. Calculate the acceleration and net force acting upon Pete Zaria. Finally, determine the coefficient of friction between Pete and the walls that would be required to support Pete's weight. PSYW
Part D: Short Computations
21. Two objects attract each other with a force of gravity (Fgrav) of 36 N. If the distance separating the objects is doubled, then what is the new force of gravitational attraction? PSYW
22. Two objects attract each other with a force of gravity (Fgrav) of 36 N. If the distance separating the objects is doubled and the masses one of the objects is tripled, then what is the new force of gravitational attraction? PSYW
23. Two objects attract each other with a force of gravity (Fgrav) of 36 N. If the distance separating the objects is increased by a factor of 4 and the masses of both objects are tripled, then what is the new force of gravitational attraction? PSYW
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
24. Suppose that the acceleration of gravity on the surface of planet X is 12 m/s/s. Determine the acceleration of gravity at a location ...
- of 2 radii from the center of planet X.
- of 4 radii from the center of planet X.
- of 2 radii from the surface of planet X.
- on the surface of planet X if the planet mass were twice as large (same radius).
- on the surface of planet X if the planet mass were one-half as large (same radius).
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
25. Suppose that a planet was located 12.0 times further from the sun than the earth's distance from the sun. Determine the period of the planet. PSYW
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
26. The acceleration of gravity on the moon is approximately one-sixth the value on earth's surface. If a person weighs 60.0 N on the moon's surface, what is his/her approximate mass on Earth? PSYW
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
27. Determine the force of gravitational attraction between a 52.0-kg mother and a 3.0-kg child if their separation distance is 0.50 meters. PSYW
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
28. Use the following information to determine the orbital velocity at treetop level on the surface of the moon. PSYW
Mass of moon = 7.36 x 1022 kg
Radius of Moon = 1.74 x 106 m
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
Part E: Problem-Solving
29. A roller coaster car loaded with passengers, has a mass of 500. kg; the radius of curvature of the track at the bottom point of a dip is 12.0 m. The vehicle has a speed of 18.0 m/s at this point.
- In the space below, draw a free-body diagram for the car (label forces according to type).
- Calculate the acceleration and the net force acting upon the car. PSYW
- Calculate the force exerted on the vehicle by the track? PSYW
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
30. What is the acceleration of a piece of dust on an old-fashioned record album, 15 cm from the center, if the record is spinning at 33.3 rpm?
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
31. What is the tension in a 0.500 meter rope which carries a 2.50 kg bucket of water in a vertical circle with a velocity of 3.00 m/s when the bucket is at the bottom of its swing?
32. A 53.5-kg rider on a roller coaster car is moving 10.3 m/s at the top of a loop which has a radius of curvature of 7.29 m. Determine the normal force experienced by the rider.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
33. Determine the minimum coefficient of friction required to keep a 920.-kg car on a turn with a radius of 26.8 m. The car is traveling 29.9 m/s and the roadway is level.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
34. With what speed (in mi/hr) must you drive your car across the crest of a hill of radius 37.1-m in order to feel weightless (1.00 m/s = 2.24 mi/hr)?
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
35. What is the reading of a bathroom scale when a man of mass 72 kg stands on it while riding in an elevator accelerating upwards at 5.4 m/s2?
36. An airplane pilot makes a vertical loop with a 56-2-m radius. Determine the normal force acting upon the pilot's 62.6-kg body at the top of the loop if his air speed is 64.1 m/s.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
37. Use the following information to help determine the acceleration of the planet Pluto about the sun.
Mass of Sun = 1.991 x 1030 kg
Sun-Pluto Distance = 5.91 x 1012 m
38. What is the period of rotation of Venus in earth years if it is a distance of 1.08 x 1011 meters from the sun? (The earth-sun distance is 1.5 x 1011 m.)
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
39. What is the gravitational attraction between the proton and electron in an Hydrogen atom if they are 5.3 x 10-11 meters apart? (mproton = 1.67 x 10-27 kg; melectron = 9.11x10-31 kg)
40. Use the following information to help determine the orbital velocity and orbital period of a satellite at a location of 15000 miles above the surface of the earth.
Mass of Earth = 5.98 x 1024 kg
Radius of Earth = 6.37 x 106 m
1609 m = 1.00 mi
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 ]
Navigate to:
Review Session Home - Topic Listing
Circular Motion and Gravitation - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-14 || #15-28 || #29-40
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Circular Motion and Gravitation
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 2 of the series includes topics in Circular Motion and Gravitation.
Visit: MOP the App Home || MOP the App - Part 2