Momentum and Collisions Review
Navigate to:
Review Session Home - Topic Listing
Momentum and Collisions - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-5 || #6-36 || #37-56 || 57-72
Part C: Diagramming and Analysis
For Questions #37-#40: Consider the before- and after-collision momentum vectors in the diagram below. Determine the magnitude and direction of the system momentum before and after the collision and identify whether or not momentum is conserved. Finally, determine the magnitude and direction of the net external impulse encountered by the system during the collision.
|
37.
|
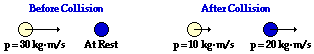
|
|
System Momentum Before Collision:
|
30 kg•m/s, right
|
|
System Momentum After Collision:
|
30 kg•m/s, right
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N
|
|
Answer: See table above.
Before the collision, the two momentum values can be added: 30 units + 0 = 30 units. (An object at rest has zero momentum.) After the collision, the momentum vectors can be added: 30 units + 0 = 30 units. In each case, the total momentum is in the direction of the arrows. Since the total system momentum before the collision is the same as it is after the collision, the total momentum of the system can be considered to be conserved. As such, there is no net external impulse upon the system. It is considered isolated.
|
|
38.
|
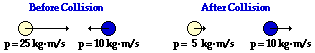
|
|
System Momentum Before Collision:
|
15 kg•m/s, right
|
|
System Momentum After Collision:
|
15 kg•m/s, right
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N•s |
|
Answer: See table above.
The dark ball has a leftward momentum, so its momentum must be assigned a - sign to distinguish its momentum from the rightward momentum of the light-colored ball. So before the collision, the system has +25 units + -10 units of momentum - a total of +15 units. After the collision, the total momentum of the system is + 15 units (the "+" is the designated sign for a rightward momentum). Since the system momentum is the same before as after the collision, momentum is conserved and the system is considered isolated from net external impulses.
|
|
39.
|
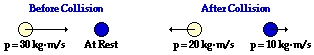
|
|
System Momentum Before Collision:
|
30 kg•m/s, right
|
|
System Momentum After Collision:
|
10 kg•m/s, left
|
|
Is momentum conserved?
|
No
|
|
Net External Impulse During Collision:
|
40 N•s, left
|
|
Answer: See table above.
Since the light-colored ball has a leftward momentum, the leftward direction will be designated as the negative direction. Thus, the before- and after-collision calculations are:
Before: +30 units + 0 units = +30 units
After: -20 units + 10 units = -10 units
The total momentum of the system has changed by -40 units. Thus, momentum is not conserved and the system experiences a net external impulse of -40 units or 40•N s, leftward.
|
|
40.
|
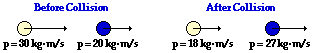
|
|
System Momentum Before Collision:
|
50 kg•m/s, right
|
|
System Momentum After Collision:
|
45 kg•m/s, right |
|
Is momentum conserved?
|
No |
|
Net External Impulse During Collision:
|
5 N•s, left
|
|
Answer: See table above.
The summations of system momentum before and after the collision are:
Before: +30 units + +20 units = +50 units.
After: +18 units + +27 units = +45 units.
The system loses 5 units of momentum. Thus, momentum is not conserved. There must be a net external impulse of -5 units upon the system. That impulse is 5 N•s, left. (The left is equivalent to saying negative.)
|
For Questions #41-#44: Repeat the procedure performed in Questions #37-#40. Note that these diagrams give velocity and mass values before and after the collision.
|
41.
|
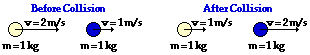
|
|
System Momentum Before Collision:
|
3 kg•m/s, right
|
|
System Momentum After Collision:
|
3 kg•m/s, right
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N•s
|
|
Answer: See table above.
Before Collision: 1 kg) * (+2 m/s) + (1 kg) * (1 m/s ) = 3 kg m/s
After Collision: (1 kg) * (1 m/s) + (1 kg) * (2 m/s ) = 3 kg m/s
The total system momentum is the same before and after the collision. Thus, momentum is conserved and there is no net external impulse on the system.
|
|
42.
|
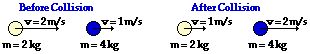
|
|
System Momentum Before Collision:
|
8 kg•m/s, right
|
|
System Momentum After Collision:
|
10 kg•m/s, right
|
|
Is momentum conserved?
|
No
|
|
Net External Impulse During Collision:
|
2 N•s, right
|
|
Answer: See table above.
Before Collision: (2 kg) * (2 m/s) + (4 kg) * (1 m/s ) = 8 kg m/s
After Collision: (1 kg) * (2 m/s) + (4 kg) * (2 m/s ) = 10 kg m/s
The total system momentum is NOT the same before and after the collision. Thus, momentum is NOT conserved. There is a net external impulse on the system which is equal to the momentum change of the system. The net external impulse is +2 kg•m/s.
|
|
43.
|
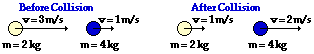
|
|
System Momentum Before Collision:
|
10 kg•m/s, right
|
|
System Momentum After Collision:
|
10 kg•m/s, right
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N•s
|
|
Answer: See table above.
Before Collision: (2 kg) * (3 m/s) + (4 kg) * (1 m/s ) = 10 kg m/s
After Collision: (2 kg) * (1 m/s) + (4 kg) * (2 m/s ) = 10 kg m/s
The total system momentum is the same before and after the collision. Thus, momentum is conserved and there is no net external impulse on the system.
|
|
44.
|
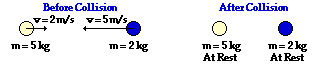
|
|
System Momentum Before Collision:
|
0 kg•m/s
|
|
System Momentum After Collision:
|
0 kg•m/s
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N•s
|
|
Answer: See table above.
Before Collision: (5 kg) * (2 m/s) + (2 kg) * (-5 m/s ) = 0 kg m/s
After Collision: (5 kg) * (0 m/s) + (2 kg) * (0 m/s ) = 0 kg m/s
The total system momentum is the same before and after the collision. Thus, momentum is conserved and there is no net external impulse on the system.
|
For Questions #45-#49, determine the unknown velocity value. Assume that the collisions occur in an isolated system.
|
General Note about Questions #45-#49:
In each of these problems, an expression for the total momentum before the collision is written by summing the product of mass and velocity for each object. The same is done with the total momentum after the collision. One must be careful to assign a negative momentum to any object which is moving leftward. When the velocity of an object is not known, the variable v should be placed in the expression in place of the actual velocity value. The two expressions for total momentum before and after the collision are set equal to each other and algebraic operations are used to determine the unknown velocities. This method is shown below.
|
|
45.
|
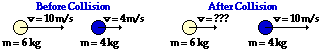
|
|
Answer: 6 m/s
Before Collision: (6 kg) * (10 m/s) + (4 kg) * (4 m/s ) = 76 kg m/s
After Collision: (6 kg) * v + (4 kg) * (10 m/s ) = (6 kg) * v + 40 kg m/s
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
76 = 6v + 40
36 = 6v
v = 6 m/s
|
|
46.
|
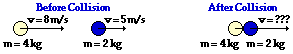
|
|
Answer: 7 m/s
Before Collision: (4 kg) * (8 m/s) + (2 kg) * (5 m/s ) =
After Collision: (4 kg) * v + (2 kg) * v
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
42 = 6 * v
v = 7 m/s
|
|
47.
|
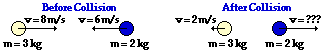
|
|
Answer: 9 m/s
Before Collision: (3 kg) * (8 m/s) + (2 kg) * (-6 m/s ) = 12 kg m/s
After Collision: (3 kg) * (-2 m/s) + (2 kg) * v = -6 kg m/s + (2 kg) * v
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
12 = -6 + 2v
18 = 2v
v = 9 m/s
|
[ [ #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 ] ]
|
48.
|
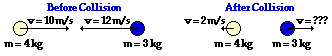
|
|
Answer: 4 m/s
Before Collision: (4 kg) * (10 m/s) + (3 kg) * (-12 m/s ) = 4 kg m/s
After Collision: (4 kg) * (-2 m/s) + (3 kg) * v = -8 kg m/s+ (3 kg) * v
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
4 = -8 + 3v
12 = 3v
v = 4 m/s
|
[ [ #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 ] ]
|
49.
|
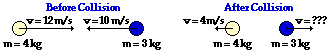
|
|
Answer: 11.3 m/s
Before Collision: (4 kg) * (12 m/s) + (3 kg) * (-10 m/s ) = 18 kg m/s
After Collision: (4 kg) * (-4 m/s) + (3 kg) * v = -16 kg m/s + (3 kg) * v
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
18 = -16 + 3v
34.0 = 3v
v = 11.3 m/s
|
For Questions #50-#52, determine the total kinetic energy of the system before and after the collision and identify the collision as being either perfectly elastic, partially inelastic/elastic or perfectly inelastic.
|
50.
|
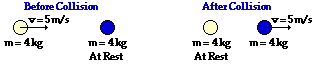
|
|
Total System Kinetic Energy Before Collision:
|
50 J
|
|
Total System Kinetic Energy After Collision:
|
50 J
|
|
Perfectly Elastic, Partially Inelastic/Elastic or Perfectly Inelastic?
|
Perfectly Elastic
|
|
Answer: See table above.
Before Collision: KEtotal = 0.5•(4 kg)•(5 m/s)2 + 0.5•(4 kg)•(0 m/s)2 = 50 J
After Collision: KEtotal = 0.5•(4 kg)•(0 m/s)2 + 0.5•(4 kg)•(5 m/s)2 = 50 J
The system kinetic energy is conserved in this collision. That is, the total kinetic energy is the same before the collision as after the collision. The critical requirement for a collision to be perfectly elastic is that the total system kinetic energy is conserved. Thus, this collision is a perfectly elastic collision.
|
|
51.
|
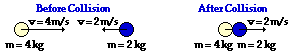
|
|
Total System Kinetic Energy Before Collision:
|
36 J
|
|
Total System Kinetic Energy After Collision:
|
12 J
|
|
Perfectly Elastic, Partially Inelastic/Elastic or Perfectly Inelastic?
|
Perfectly Inelastic
|
|
Answer: See table above.
Before Collision: KEtotal = 0.5•(4 kg)•(4 m/s)2 + 0.5•(2 kg)•(-2 m/s)2 = 36 J
After Collision: KEtotal = 0.5•(4 kg)•(2 m/s)2 + 0.5•(2 kg)•(2 m/s)2 = 12 J
The system kinetic energy is NOT conserved in this collision. That is, the total kinetic energy is NOT the same before the collision as after the collision. The critical requirement for a collision to be perfectly inelastic is that the colliding objects move as a single unit with the same velocity after the collision. These objects do "stick together" after the collision and move as a single unit at the same velocity. Thus, the collision is a perfectly inelastic collision.
[ [ #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 ] ]
|
|
52.
|
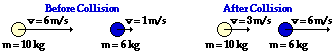
|
|
Total System Kinetic Energy Before Collision:
|
183 J
|
|
Total System Kinetic Energy After Collision:
|
153 J |
|
Perfectly Elastic, Partially Inelastic/Elastic or Perfectly Inelastic?
|
Partially Inelastic/Elastic
|
|
Answer: See table above.
Before Collision: KEtotal = 0.5•(10 kg)•(6 m/s)2 + 0.5•(6 kg)•(1 m/s)2 = 183 J
After Collision: KEtotal = 0.5•(10 kg)•(3 m/s)2 + 0.5•(6 kg)•(6 m/s)2 = 153 J
The system kinetic energy is NOT conserved in this collision. That is, the total kinetic energy is NOT the same before the collision as after the collision. Thus, the collision does not meet the criterion for a perfectly elastic collision. The objets do NOT "stick together" after the collision; they move with different speeds. Thus, the collision does not meet the criterion for a perfectly inelastic collision. This collision is a partially inelastic/elastic collision.
|
Part D: Qualitative Relationships Between Variables
53. An object with a mass M and a velocity v has a momentum of 32 kg•m/s. An object with a mass of ...
- .. 2M and a velocity of 2v would have a momentum of 64 kg•m/s.
- ... 2M and a velocity of 0.5v would have a momentum of 32 kg•m/s.
- ... 0.5M and a velocity of 2v would have a momentum of 32 kg•m/s.
- ... 0.5M and a velocity of 0.5v would have a momentum of 8 kg•m/s.
- ... 4M and a velocity of v would have a momentum of 128 kg•m/s.
- ... 4M and a velocity of 0.5v would have a momentum of 64 kg•m/s.
- ... 0.5M and a velocity of 4v would have a momentum of 64 kg•m/s.
- ... 3M and a velocity of 2v would have a momentum of 192 kg•m/s.
|
Answer: See Answers above.
Momentum is the product of mass and velocity. As such, the momentum of an object is directly proportional to the mass and directly proportional to the velocity. If the mass of an object is altered by some factor, then the momentum of the object is altered by that same factor. So if the mass is doubled, the momentum is doubled; the new value would be two times the original value. And if the mass is tripled, then the momentum is tripled; the new value would be three times the original value. If the velocity of an object is altered by some factor, then the momentum of the object is altered by that same factor. So if the velocity is doubled, the momentum is doubled; the new value would be two times the original value. And if the velocity is tripled, then the momentum is tripled; the new value would be three times the original value. This is shown in the work below.
a. New value = 32 kg m/s • 2 • 2 = 128 kg•m/s
b. New value = 32 kg m/s • 2 • 0.5 = 32 kg•m/s
c. New value = 32 kg m/s • 0.5 • 2 = 32 kg•m/s
d. New value = 32 kg m/s • 0.5 • 0.5 = 8 kg•m/s
e. New value = 32 kg m/s • 4 • 1 = 128 kg•m/s
f. New value = 32 kg m/s • 4 • 0.5 = 64 kg•m/s
g. New value = 32 kg m/s • 0.5 • 4 = 64 kg•m/s
h. New value = 32 kg m/s • 3 • 2 = 192 kg•m/s
|
54. An object with a mass M and a velocity v undergoes a collision and encounters a force of F for a time of t. The collision brings the object to a final rest position ...
- ... If the object had a mass of 2M and a velocity of v, then it would need an impulse which is 2 F•t in order to be brought to rest.
- ... If the same object encountered a force of 2F, then it would bring it to rest in a time of 0.5 t, The impulse would be the same size and the momentum change would be the same size.
- ... If the same object encountered a force of 10F, then it would bring it to rest in a time of 0.1 t, The impulse would be the same size and the momentum change would be the same size.
- ... If the same object encountered a force of 0.2F, then it would bring it to rest in a time of 5 t, The impulse would be the same (size and the momentum change would be the same size.
- ... If the object had a mass of 2M and a velocity of v encountered a force of 4F, then it would be brought to rest in a time of 0.5 t. The impulse would be 2 times the original impulse and the momentum change would be 2 times the original impulse.
- ... If the object had a mass of 2M and a velocity of 2v encountered a force of 4F, then it would be brought to rest in a time of 1.0 t. The impulse would be 4 times the original impulse and the momentum change would be 4 times the original impulse.
- ... If the object had a mass of 0.5M and a velocity of 4v encountered a force of 2F, then it would be brought to rest in a time of 1.0 t. The impulse would be 2 times the original impulse and the momentum change would be 2 times the original impulse.
|
Answer: See Answers above.
In a collision, the impulse encountered by an object causes and is equal to the momentum change of the object. For objects being brought to rest, the change in momentum is simply equal to the original momentum. An object with twice the momentum would require twice the impulse to stop it. An object with one-half the momentum would require one-half the impulse to stop it. The momentum is the product of mass and velocity, so any alteration in the mass or the velocity or both would alter the required impulse by that same factor. The impulse results from a force acting over time and is the product of force and time. So twice the impulse can be achieved by the same force acting for twice the time or twice the force acting for the same time or even one-half the force acting for four times the time. These principles are illustrated below.
a. Two times the mass means two times the original momentum. Two times the impulse would be required to stop an object with two times the momentum.
b. If the same object with the same momentum (M•v) were stopped by twice the original force, then only one-half the original time would be required to stop it. Since the momentum change has not been altered in this case (an object with a momentum of M•v is still being stopped), the impulse is not altered either.
c. If the same object with the same momentum (M•v) were stopped by ten times the original force, then only one-tenth the original time would be required to stop it. Since the momentum change has not been altered in this case (an object with a momentum of M•v is still being stopped), the impulse is not altered either.
d. If the same object with the same momentum (M•) were stopped by one-fifth the original force, then five times the original time would be required to stop it. Since the momentum change has not been altered in this case (an object with a momentum of M•v is still being stopped), the impulse is not altered either.
e. If an object with twice the mass is being stopped, then twice the momentum change would occur. Two times the momentum change means that an impulse which is two times the original impulse would be required. To achieve two times the impulse, the product of force and time must be doubled. Since the force is four times bigger, the time needs to be one-half the original time.
f. If an object with twice the mass and twice the velocity is being stopped, then four times the momentum change would occur. Four times the momentum change means that an impulse which is four times the original impulse would be required. To achieve four times the impulse, the product of force and time must be quadrupled. Since the force is four times bigger, the time needs to be the same as the original time.
g. If an object with one-half the mass and four times the velocity is being stopped, then twice the momentum change would occur. Two times the momentum change means that an impulse which is two times the original impulse would be required. To achieve two times the impulse, the product of force and time must be doubled. Since the force is two times bigger, the time needs to be the same as the original time.
|
55. Two carts are placed next to each other on a low-friction track. The carts are equipped with a spring-loaded mechanism which allows them to impart an impulse to each other. Cart A has a mass of M and Cart B has a mass of M. The spring-loaded mechanism is engaged and then released. The impulse causes Cart A to be propelled forward with a velocity of 40 cm/s.
- Cart B will be propelled backward with a velocity of 40 cm/s.
- ... If Cart B had a mass of 2M then it would be propelled backwards with a velocity of 20 cm/s.
- ... If Cart B had a mass of 0.5M then it would be propelled backwards with a velocity of 80 cm/s.
- ... If Cart B has a mass of 2M then it would be propelled backwards with a momentum which is the same as the original momentum.
- ... If Cart B has a mass of 2M then it would encounter an impulse which is the same as the original impulse.
|
Answer: See Answers above.
Cart A and Cart B begin at rest. The original momentum of the system is 0 units. If momentum is to be conserved, the total momentum of the system of two carts must also be 0 units. This means that the momentum of Cart A must have the same magnitude as the momentum of Cart B. That is, after the spring is released, the product of mass and velocity for Cart A must equal the product of mass and velocity for Cart B. This principle is illustrated in the reasoning below.
a. Since the two carts have the same mass, they must also have the same velocity in order to have the same magnitude of momentum. The post-explosion velocity of Cart B is 40 cm/s.
b. If Cart B has twice the mass as Cart A, then it must be propelled backwards with one-half the velocity. The post-explosion velocity of Cart B is 20 cm/s.
c. If Cart B has one-half the mass As Cart A, then it must be propelled backwards with two times the velocity. The post-explosion velocity of Cart B is 80 cm/s.
d. Changing the mass of either one of the carts does not alter the impulse or the momentum change which it experiences. An alteration in the mass merely alters the velocity with which the cart is propelled. A twice-as-massive cart acquires one-half the original velocity but the momentum change is the same as the original momentum change.
e. Changing the mass of either one of the carts does not alter the impulse or the momentum change which it experiences. An alteration in the mass merely alters the velocity with which the cart is propelled. A twice-as-massive cart acquires one-half the original velocity but the impulse is the same as the original impulse.
|
56. A cart with a mass of M is moving along a low-friction track with a speed of 60 cm/s. A brick is gently dropped from rest upon the cart. After the collision the cart and brick move together.
- ... If the brick has a mass of 2M, then the post-collision speed of the two objects will be 20 cm/s.
- ... If the brick has a mass of 3M, then the post-collision speed of the two objects will be 15 cm/s.
- ... If the brick has a mass of 4M, then the post-collision speed of the two objects will be 12 cm/s.
- ... If the brick has a mass of 5M, then the post-collision speed of the two objects will be 10 cm/s.
- ... If the brick has a mass of 0.5M, then the post-collision speed of the two objects will be 40 cm/s.
- ... If the brick has a mass of 0.25M, then the post-collision speed of the two objects will be 48 cm/s.
|
Answer: See Answers above.
This is a special case of a perfectly inelastic collision. The total system momentum before the collision is possessed solely by the moving cart. After the collision, the total system momentum is the combined momentum of the brick and the cart. Since the brick and cart travel at the same velocity after the collision, the momentum is simply the sum of their masses multiplied by their velocity. In effect, the total mass which is in motion is increased by some factor as a result of the subsequent motion of the brick. For momentum to be conserved, the velocity of the cart (and the brick which is on top of it) must be decreased by that same factor. This principle is used to reason towards the answers to these questions.
a. Adding a brick with a mass of 2M will increase the total mass in motion from M (the cart's mass) to 3M. This threefold increase in mass is accompanied by a threefold decrease in velocity. The new velocity is one-third the original value. The cart and brick move forward with a velocity of 20 cm/s.
b. Adding a brick with a mass of 3M will increase the total mass in motion from M (the cart's mass) to 4M. This fourfold increase in mass is accompanied by a fourfold decrease in velocity. The new velocity is one-fourth the original value. The cart and brick move forward with a velocity of 15 cm/s.
c. Adding a brick with a mass of 4M will increase the total mass in motion from M (the cart's mass) to 5M. This fivefold increase in mass is accompanied by a fivefold decrease in velocity. The new velocity is one-fifth the original value. The cart and brick move forward with a velocity of 12 cm/s.
d. Adding a brick with a mass of 5M will increase the total mass in motion from M (the cart's mass) to 6M. This six-fold increase in mass is accompanied by a six-fold decrease in velocity. The new velocity is one-sixth the original value. The cart and brick move forward with a velocity of 10 cm/s.
e. Adding a brick with a mass of 0.5M will increase the total mass in motion from M (the cart's mass) to 1.5M. This increases the mass by a factor of 1.5 and is accompanied by a decrease in velocity by a factor of 1.5. The new velocity is two-thirds the original value. The cart and brick move forward with a velocity of 40 cm/s.
f. Adding a brick with a mass of 0.25M will increase the total mass in motion from M (the cart's mass) to 1.25M. This increases the mass by a factor of 1.25 and is accompanied by a decrease in velocity by a factor of 1.25. The new velocity is four-fifths the original value. The cart and brick move forward with a velocity of 48 cm/s.
|
[ [ #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 ] ]
Navigate to:
Review Session Home - Topic Listing
Momentum and Collisions - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-5 || #6-36 || #37-56 || 57-72
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Momentum and Collisions
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 3 of the series includes topics in Momentum and Collisions.
Visit: MOP the App Home || MOP the App - Part 3