Momentum and Collisions Review
Navigate to:
Review Session Home - Topic Listing
Momentum and Collisions - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-5 || #6-36 || #37-56 || 57-72
Part E: Problem-Solving
57. A 0.530-kg basketball hits a wall head-on with a forward speed of 18.0 m/s. It rebounds with a speed of 13.5 m/s. The contact time is 0.100 seconds. (a) determine the impulse with the wall, (b) determine the force of the wall on the ball.
|
Answer: Answer: (a) -16.7 N s; (b) -167 N
Given: m = 0.530 kg; vi = 18.0 m/s; vf = 13.5 m/s; t = 0.100 s
Find: (a) Impulse, (b) Force
(a) Impulse = Momentum Change = m•Delta v = m•(vf - vi)= (0.530 kg)•( -13.5 m/s - 18.0 m/s)
Impulse = -16.7 kg•m/s = -16.7 N•s
where the "-" indicates that the impulse was opposite the original direction of motion.
(Note that a kg•m/s is equivalent to a N•s)
(b) The impulse is the product of force and time. So if impulse is known and time is known, force can be easily determined.
Impulse = F•t
F = Impulse/t = (-16.7 N s) / (0.100 s) = -167 N
where the "-" indicates that the impulse was opposite the original direction of motion.
|
58. A 4.0-kg object has a forward momentum of 20. kg•m/s. A 60. N•s impulse acts upon it in the direction of motion for 5.0 seconds. A resistive force of 6.0 N then impedes its motion for 8.0 seconds. Determine the final velocity of the object.
|
Answer: vf = 8.0 m/s
This question is best thought about conceptually using the principle that an objects momentum is changed when it encounters an impulse and the amount of change in momentum is equal to the impulse which it encounters.
Here an object starts with 20 units (kg•m/s) of momentum. It then encounters an impulse of 60 units (N•s) in the direction of motion. A 60-unit impulse will change the momentum by 60 units, either increasing or decreasing it. If the impulse is in the direction of an object's motion, then it will increase the momentum. So now the object has 80 units (kg•m/s) of momentum. The object then encounters a resistive force of 6.0 N for 8.0 s. This is equivalent to an impulse of 48 units (N•s). Since this impulse is "resistive" in nature, it will decrease the object's momentum by 48 units. The object now has 32 units of momentum. The question asks for the object's velocity after encountering these two impulses. Since momentum is the product of mass and velocity, the velocity can be easily determined.
p = m•v
vfinal = pfinal / m = (32 kg m/s) / (4.0 kg) = 8.0 m/s
|
59. A 3.0-kg object is moving forward with a speed of 6.0 m/s. The object then encounters a force of 2.5 N for 8.0 seconds in the direction of its motion. The object then collides head-on with a wall and heads in the opposite direction with a speed of 5.0 m/s. Determine the impulse delivered by the wall to the object.
|
Answer: 53 N•s
Like the previous problem, this problem is best solved by thinking through it conceptually using the impulse-momentum change principle.
Here the object begins with a momentum of 18 units (kg•m/s). The object encounters a force of 2.5 N for 8.0 seconds. This is equivalent to an impulse of 20 units (N•s). Since this impulse acts in the direction of motion, it changes the object's momentum from 18 units to 38 units. A final impulse is encountered when colliding with a wall. Upon rebounding, the object has a momentum of -15 units (kg•m/s). The -15 is the product of mass (3 kg) and velocity (-5 m/s). The "-" sign is used since the object is now moving in the opposite direction as the original motion. The collision with the wall changed the object's momentum from +38 units to -15 units. Thus, the collision must have resulted in a 53-unit impulse since it altered the object's momentum by 53 units.
|
60. A 46-gram tennis ball is launched from a 1.35-kg homemade cannon. If the cannon recoils with a speed of 2.1 m/s, determine the muzzle speed of the tennis ball.
|
Answer: 62 m/s
Given: mball = 46 g = 0.046 kg; mcannon = 1.35 kg; vcannon = -2.1 m/s
Find: vball = ???
The ball is in the cannon and both objects are initially at rest. The total system momentum is initially 0. After the explosion, the total system momentum must also be 0. Thus, the cannon's backward momentum must be equal to the ball's forward momentum.
mcannon • vcannon = -mball • vball
(1.35 kg) • (-2.1 m/s) = (0.046 kg) • vball
vball = (1.35 kg) • (2.1 m/s) / (0.046 kg) = 61.63 m/s = ~62 m/s
|
61. A 2.0-kg box is attached by a string to a 5.0-kg box. A compressed spring is placed between them. The two boxes are initially at rest on a friction-free track. The string is cut and the spring applies an impulse to both boxes, setting them in motion. The 2.0-kg box is propelled backwards and moves 1.2 meters to the end of the track in 0.50 seconds. Determine the time it takes the 5.0-kg box to move 0.90 meters to the opposite end of the track.
|
Answer: 0.94 s
For the sake of the discussion, the 2-kg box will be referred to as Box 1 and the 5-kg box will be referred to as box 2.
Given: mbox 1 = 2.0 kg; mbox 2 = 5.0 kg; dbox 1 = 1.2 m; tbox 1 = 0.50 s; dbox 2 = 0.90 m
Find: tbox 2 = ???
The two boxes are initially at rest. The total system momentum is initially 0. After the cutting of the string and the impulse of the spring, the total system momentum must also be 0. Thus, Box 1's backward momentum must be equal to the Box 2's forward momentum. The distance and time for Box 1 must be used to determine its velocity.
v = d/t = (1.2 m) / (0.5 s) = 2.4 m/s
Now the principle of momentum conservation can be used to determine Box 2's velocity.
mbox 1 • vbox 1 = mbox 2 • vbox 2
(2 kg) • (2.4 m/s) = (5 kg) • vbox 2
vbox 2 = (2 kg) • (2.4 m/s) / (5 kg) = 0.96 m/s
The velocity of Box 2 can be used to determine the time it takes it to move a distance of 0.90 meters.
vbox 2 = dbox 2 / time
Time = dbox 2 / vbox 2 = (0.90 m) / (0.96 m/s) = 0.9375 s = ~0.94 s
|
62. Two children are playing with a large snowball while on ice skates on a frozen pond. The 33-kg child tosses the 5.0-kg snowball, imparting a horizontal speed of 5.0 m/s to it. The 33-kg child is 4.0 meters from a 28-kg child and 8.0 meters from the edge of the pond (located behind him). Assuming negligible friction, how much time elapses between when the 28-kg child gets hit by the snowball and when the 33-kg child reaches the edge of the pond?
|
Answer: 9.8 s
For the sake of the discussion, we will refer to the 33-kg child as the "thrower" and the 28-kg child as the "catcher."
In this scenario, the thrower tosses a snowball forward towards the catcher. This throwing action involves an impulse imparted to the snowball. And due to action-reaction, there is an identical impulse imparted to the thrower which causes the thrower to be set in motion in the opposite direction. The impulse is equal to the momentum change. And since the mass and the velocity change of the snowball are known, the momentum change of the snowball can be determined.
m • (Delta v)snowball = m • (vfinal-snowball - vinitial-snowball)
m • (Delta v)snowball = (5.0 kg) • (+ 5.0 m/s - 0 m/s) = 25.0 kg•m/s
This 25-unit momentum change of the snowball is equal to the thrower's momentum change. Thus the thrower is moving backwards towards the edge of the pond with a momentum of -25.0 kg•m/s. Since momentum is related to velocity, the post-impulse velocity can be determined.
pthrower = mthrower • vthrower
vthrower = pthrower / mthrower
vthrower = (-25.0 kg•m/s) / (33 kg)
vthrower = -0.7576 m/s
The thrower began 8.0 meters from the edge of the pond. Once the ball has been thrown, the thrower is moving backwards towards the edge of the pond with a speed of 0.7576 m/s. Assuming negligible friction on the icy pond, the speed can be used to determine the time that elapses between when the ball is thrown and when the thrower reaches the pond's edge.
v = d/t
t = d / v
tfor thrower to reach pond's edge = (8.0 meters) / (0.7576 m/s)
tfor thrower to reach pond's edge = 10.56 seconds
Once the ball is thrown, the thrower starts moving backwards towards the pond's edge. Meanwhile, the ball is moving forward towards the catcher. The time for the ball to move from the thrower's original position to the catcher is dependent upon the ball's speed and the original distance between the thrower and the catcher.
v = d/t
t = d / v
tfor ball to move from thrower to catcher = (4.0 meters) / (5.0 m/s)
tfor ball to move from thrower to catcher = 0.800 seconds
The instant the ball is thrown, two motions occur - the ball moves forward towards the catcher and the thrower moves backwards towards the pond's edge. The ball reaches the catcher in 0.800 seconds. And 9.76 seconds (~9.8 s) later (10.56 s - 0.80 s), the thrower reaches the pond's edge.
|
63. A 2.8-kg physics cart is moving forward with a speed of 45 cm/s. A 1.9-kg brick is dropped from rest and lands on the cart. The cart and brick move together across the horizontal surface. Assume an isolated system.
a. Determine the post-collision speed of the cart and the brick.
b. Determine the momentum change of the cart.
c. Determine the momentum change of the brick.
d. Determine the net impulse upon the cart.
e. Determine the net impulse upon the system of cart and brick.
|
Answers: (a) v = 27 cm/s
(b) Delta pcart = -51 kg • cm/s
(c)Delta pbrick = +51 kg • cm/s
(d) Impulse on cart = -51 kg • cm/s
(e) Impulse on brick = +51 kg • cm/s
Before the collision, only the moving cart has momentum. The total momentum of the system is simply the mass of the cart multiplied by the velocity of the cart.
ptotal-before = pcart = mcart • vcart-before
ptotal-before = (2.8 kg) • (45 cm/s)
ptotal-before = 126 kg • cm/s
The collision is perfectly inelastic; the two objects stick together and move as a single unit. After the collision, the total momentum of the system is the sum of the individual momentum values.
ptotal-after = pcart-after + pbrick-after
ptotal-after = mcart-after • vcart-after + mbrick • vbrick-after
ptotal-after = mcart-after • v + mbrick • v
ptotal-after = (2.8 kg) • v + (1.9 kg) • v
ptotal-after = (4.7 kg) • v
Assuming an isolated system, total system momentum is conserved. Thus, before- and after-collision momentum expressions can be set equal to each other, and the equation can be manipulated to solve for the post-collision speed of the two objects.
126 kg • cm/s = (4.7 kg) • v
v = (126 kg • cm/s) / (4.7 kg)
v = 26.809 cm/s (~27 cm/s)
The momentum change of the cart (Delta pcart) is simply the difference between the initial and final momentum values.
Delta pcart = pcart-after - pcart-before
Delta pcart = mcart-after • vcart-after - mcart • vcart-before
Delta pcart = (2.8 kg) • (26.809 m/s) - (2.8 kg) • (45 cm/s)
Delta pcart = -50.936 kg • cm/s (~51 kg•cm/s)
During the collision, the cart loses 50.9 units of momentum. Since total system momentum is conserved, the brick must gain the same quantity of momentum.
Delta pbrick = 50.936 kg • cm/s (~51 kg•cm/s)
The change in momentum of the cart is due to the fact that an impulse acts upon the cart during the collision. The moment contact is made between the brick and the cart, the two objects are moving at different speeds relative to each other. Consequently, there will be a friction force acting between the two surfaces until the two objects maintain the same speed. That is, the brick will pull backward upon the moving cart in order to slow it down; and the moving cart will pull forward upon the stationary brick in order to speed it up. These impulses are what cause the momentum changes. And these impulses are equal to the momentum changes. Thus,
Impulse on cart = Delta pcart = -50.936 kg • cm/s (~51 kg•cm/s)
Impulse on brick = Delta pbrick = +50.936 kg • cm/s (~51 kg•cm/s)
|
64. In a physics lab, a 0.500-kg cart moving at 36.4 cm/s collides inelastically with a second cart which is initially at rest. The two carts move together with a speed of 21.8 cm/s after the collision. Determine the mass of the second cart.
|
Answer: ~ 0.335 kg
This problem involves a perfectly inelastic collision between two carts. Thus, the post-collision velocity of the two carts are identical. For communication sake, the carts will be referred to as Cart A and Cart B. The given information is:
mA = 0.500 kg; vA-before = 36.4 cm/s; vB-before = 0 cm/s; vA-after = 21.8 cm/s; vB-after = 21.8 cm/s
The unknown to be solved for in this problem is the mass of Cart B (mB).
The solution begins by setting the writing expressions for the total momentum of the system before and after the collision.
Before Collision: ptotal-before = (0.500 kg)•(36.4 cm/s) + (mB)•(0 cm/s)
After Collision: ptotal-after = (0.500 kg)•(21.8 cm/s) + (mB)•(21.8 cm/s)
Assuming momentum conservation, these expressions are set equal to each other and then algebraically manipulated to solve for the unknown (mB).
(0.500 kg)•(36.4 cm/s) + (mB)•(0 cm/s) = (0.500 kg)•(21.8 cm/s) + (mB)•(21.8 cm/s)
(0.500 kg)•(36.4 cm/s) = (0.500 kg)•(21.8 cm/s) + (mB)•(21.8 cm/s)
(0.500 kg)•(36.4 cm/s) - (0.500 kg)•(21.8 cm/s) = (mB)•(21.8 cm/s)
(7.30 kg•cm/s) = (mB)•(21.8 cm/s)
0.33486 kg = mB
mB = ~0.335 kg
|
65. A 9230-kg truck collides head on with a 1250-kg parked car. The vehicles entangle together and slide a linear distance of 10.6 meters before coming to rest. Assuming a uniform coefficient of friction of 0.820 between the road surface and the vehicles, determine the pre-collision speed of the truck.
|
Answer: 14.8 m/s
Here is an example of a more difficult problem involving the combination of momentum principles with information learned in other units of the course. The problem involves a perfectly inelastic collision between a truck and a car. Thus, the post-collision velocity of the truck and car are identical. The given collision information is:
mTruck = 9320 kg; mCar = 1250 kg; vCar-before = 0 cm/s; vTruck-after = vCar-after= ??
The unknown to be solved for in this problem is the velocity of the truck before the collision (vTruck-before).
There is some kinematic/dynamic information provided that will assist in determining the post-collision velocity of the entangled truck and car.
mu = 0.820; d = 10.6 m; vfinal = 0 m/s
The combination of car and truck will slide to a final resting position due to the action of friction. The coefficient of friction, a free-body diagram and a kinematic equation can be used to determine the velocity of the car and truck immediately following the collision.
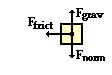 The free-body diagram is shown at the right. Note that the unbalanced force is friction. Its value is found by multiplying the coefficient of friction by the combined weight of the car and truck (mu•M•g where M = mtruck + mcar ). The force of friction is the net force. Thus, the acceleration is the force of friction divided by the combined mass of the car and the truck (M). Subsequently, the expression for the acceleration of the car and truck while sliding to a stop is simply mu•g. The free-body diagram is shown at the right. Note that the unbalanced force is friction. Its value is found by multiplying the coefficient of friction by the combined weight of the car and truck (mu•M•g where M = mtruck + mcar ). The force of friction is the net force. Thus, the acceleration is the force of friction divided by the combined mass of the car and the truck (M). Subsequently, the expression for the acceleration of the car and truck while sliding to a stop is simply mu•g.
a = Fnet/m = Ffrict/m = (mu•M•g) / M = mu•g
a = -8.036 m/s/s
(The - sign indicates a deceleration or slowing down motion.)
Now a kinematic equation can be used to solve for the velocity of the car and truck immediately after the collision. This is shown below:
vf2 = vo2 + 2•a•d
(0 m/s)2 = vo2 + 2•(-8.036 m/s/s)•(10.6 m) = vo2 - 170.36 m2/s2
(0 m/s)2 = vo2 - 170.36 m2/s2
vo2 = 170.36 m2/s2
vo = SQRT(170.36 m2/s2)
vo = 13.052 m/s (= vTruck-after = vCar-after )
Now that the post-collision velocity of the car and truck are known, expressions for the total system momentum can be written for the before- and after-collision situations.
Before Collision: ptotal-before = (9320 kg)•(vTruck-before) + (1250 kg)•(0 cm/s)
After Collision: ptotal-after = (9320 kg)•(13.052 m/s) + (1250 kg)•(13.052 m/s)
Assuming momentum conservation, these expressions are set equal to each other and then algebraically manipulated to solve for the unknown (mB).
(9320 kg)•(vTruck-before) + (1250 kg)•(0 cm/s) = (9320 kg)•(13.052 m/s) + (1250 kg)•(13.052 m/s)
(9320 kg)•(vTruck-before) = (9320 kg)•(13.052 m/s) + (1250 kg)•(13.052 m/s)
(9320 kg)•(vTruck-before) = 137963 kg•m/s
(vTruck-before) = (137963 kg•m/s) / (9320 kg)
vTruck-before = ~14.8 m/s
|
66. A classic physics demonstration involves firing a bullet into a block of wood suspended by strings from the ceiling. The height to which the wood rises below its lowest position is mathematically related to the pre-collision speed of the bullet. If a 9.7-gram bullet is fired into the center of a 1.1-kg block of wood and it rises upward a distance of 33 cm, then what was the pre-collision speed of the bullet?
|
Answer: 2.9 x 102 m/s
Here is another instance in which momentum principles must be combined with content learned in other units in order to complete an analysis of a physical situation. The collision involves the inelastic collision between a block of wood and bullet. The bulled lodges into the wood and the two objects move with identical velocity after the collision. The kinetic energy of the wood and bullet is then converted to potential energy as the combination of two objects rises to a final resting position.
Energy conservation can be used to determine the velocity of the wood-bullet combination immediately after the collision. The kinetic energy of the wood-bullet combination is set equal to the final potential energy of the wood-bullet combination and the equation is manipulated to solve for the post-collision velocity of the wood-bullet combination. The work is shown here:
0.5 • (mwood + mbullet) • vcombination-after2 = (mwood + mbullet) • (9.8 m/s2) • (0.33 m)
0.5 • vcombination-after2 = (9.8 m/s2) • (0.33 m)
vcombination-after2 = 2 •(9.8 m/s2) • (0.33 m)
vcombination-after2 = 6.468 m2/s2
vcombination-after = 2.5432 m/s
Now momentum conservation can be used to determine the pre-collision velocity of the bullet (vbullet-before). The known information is:
mwood = 1.1 kg; mbullet = 9.7 g = 0.0097 kg; vwood-after = 2.5432 m/s; vbullet-after = 2.5432 m/s
Expressions for the total system momentum can be written for the before- and after-collision situations.
Before Collision: ptotal-before = (1.1 kg)•(0 m/s) + (0.0097 kg)•(vbullet-before)
After Collision: ptotal-after = (1.1 kg)•(2.5432 m/s) + (0.0097 kg)•(2.5432 m/s)
Assuming momentum conservation, these expressions are set equal to each other and then algebraically manipulated to solve for the unknown (mB).
(1.1 kg)•(0 m/s) + (0.0097 kg)•(vbullet-before) = (1.1 kg)•(2.5432 m/s) + (0.0097 kg)•(2.5432 m/s)
(0.0097 kg)•(vbullet-before) = (1.1 kg)•(2.5432 m/s) + (0.0097 kg)•(2.5432 m/s)
(0.0097 kg)•(vbullet-before) = 2.8222 kg•m/s
vbullet-before = (2.8222 kg•m/s) / (0.0097 kg)
vbullet-before = 290.95 m/s
vbullet-before = ~2.9 x 102 m/s
|
67. At an amusement park, twin brothers Timmy (m = 50 kg) and Jimmy (m = 62 kg) occupy separate 36-kg bumper cars. Timmy gets his car cruising at 3.6 m/s and collides head-on with Jimmy who is moving the opposite direction at 1.6 m/s. After the collision, Timmy bounces backwards at 0.5 m/s. Assuming an isolated system, determine ...
a. ... Jimmy's post-collision speed.
b. ... the percentage of original kinetic energy which is lost as the result of the collision.
|
Answer: (a) v = ~2.0 m/s
(b) % KE Loss = ~70. %
(a) Expressions for the total momentum of the system before and after the collision can be written. For the before-collision expression, Timmy is assigned a positive velocity value and Jimmy is assigned a negative velocity value (since he is moving in the opposite direction). Furthermore, the mass of the bumper car must be figured into the total mass of the individually moving objects.
ptotal-before = pTimmy-before + pJimmy-before
ptotal-before = mTimmy • vTimmy-before + mJimmy • vJimmy-before
ptotal-before = (86 kg) • (3.6 m/s) + (98 kg) • (-1.6 m/s)
For the before-collision expression, Timmy is assigned a negative velocity value (since he has bounced backwards in the opposite direction of his original motion. Jimmy is assigned a velocity of v since his velocity is not known.
ptotal-after = pTimmy-after + pJimmy-after
ptotal-after = mTimmy • vTimmy-after + mJimmy • vJimmy-after
ptotal-after = (86 kg) • (-0.5 m/s) + (98 kg) • (vJimmy-after)
ptotal-after = (86 kg) • (-0.5 m/s) + (98 kg) • v
Since the system is assumed to be isolated, the before-collision momentum expression can be set equal to the after-collision momentum expression. The equation can then be algebraically manipulated to solve for the post-collision velocity of Jimmy.
(86 kg) • (3.6 m/s) + (98 kg) • (-1.6 m/s) = (86 kg) • (-0.5 m/s) + (98 kg) • v
309.6 kg•m/s - 156.8 kg•m/s = (86 kg) • (-0.5 m/s) + (98 kg) • v
152.8 kg•m/s = - 43 kg•m/s + (98 kg) • v
152.8 kg•m/s + 43 kg•m/s = (98 kg) • v
195.8 kg•m/s = (98 kg) • v
v = (195.8 kg•m/s) / (98 kg)
v = 1.998 m/s = ~2.0 m/s
(b) This collision is neither perfectly elastic (since the collision force is a contact force) nor perfectly inelastic (since the objects do not stick together). It is a partially elastic/inelastic collision. Since the collision is not perfectly elastic, there is a loss of total system kinetic energy during the collision. The before-collision and after-collision kinetic energy values can be calculated and the percentage of total KE lost can be determined.
The before-collision KE is based on before-collision speeds:
KEsystem-before = KETimmy-before + KEJimmy-before
KEsystem-before = 0.5 • mTimmy • vTimmy-before2 + 0.5 • mJimmy • vJimmy-before2
KEsystem-before = 0.5 • (86 kg) • (3.6 m/s)2 + 0.5 • (98 kg) • (1.6 m/s)2
KEsystem-before = 557.28 J + 125.44 J
KEsystem-before = 682.72 J
The after-collision KE is based on after -collision speeds:
KEsystem-after = KETimmy-after + KEJimmy-after
KEsystem-after = 0.5 • mTimmy • vTimmy-after + 0.5 • mJimmy • vJimmy-after
KEsystem-after = 0.5 • (86 kg) • (0.5 m/s)2 + 0.5 • (98 kg) • (1.998 m/s)2
KEsystem-after = 10.75 J + 195.61 J
KEsystem-after = 206.36 J
The system kinetic energy is changed from 682.72 J to 206.36 J during the collision. The total KE lost is 476.36 J. This value can be used to determine the percent of the original KE which is lost in the collision.
% KE Loss = (476.36 J) / (682.72 J) • 100%
% KE Loss = 69.77% = ~70%
|
68. Two billiard balls, assumed to have identical mass, collide in a perfectly elastic collision. Ball A is heading East at 12 m/s. Ball B is moving West at 8.0 m/s. Determine the post-collision velocities of Ball A and Ball B.
|
Answer: vA-after = -8.0 cm/s; vB-after = 12 cm/s (The - indicates West and the + indicates East)
This collision is said to be perfectly elastic. Thus, both the total system momentum and the total system kinetic energy of the two objects is conserved. The momentum conservation equation can be written as
mA • vA-before + mB • vB-before = mA • vA-after + mB • vB-after
Since the balls are identical, their masses are the same. That is, mA = mB = m. The equation can be rewritten as:
m • vA-before + m • vB-before = m • vA-after + m • vB-after
Since each term of the equation contains the variable m, we can divide through by m and cancel m's from the equation. The equation can be rewritten as:
 vA-before + vB-before = vA-after + vB-after vA-before + vB-before = vA-after + vB-after
For elastic collisions, total system kinetic energy is conserved. The kinetic energy conservation equation is written as
0.5 • m • vA-before2 + 0.5 • m • vB-before2 = 0.5 • m • vA-after2 + 0.5 • m • vB-after2
As shown in the book, this equation can be simplified to the form of
 vA-before + vA-after = vB-before + vB-after vA-before + vA-after = vB-before + vB-after
The problem states the before-collision velocities of the two balls.
vA-before = 12 cm/s (the + indicates east)
vB-before = - 8 cm/s (the - indicates west)
These two values can be substituted into equations 1 and 2 above.
 12 cm/s - 8 cm/s = vA-after + vB-after 12 cm/s - 8 cm/s = vA-after + vB-after
 12 cm/s + vA-after = - 8 cm/s + vB-after 12 cm/s + vA-after = - 8 cm/s + vB-after
Now the problem has been reduced to two equations and two unknowns. Such a problem can be solved in numerous ways. One method involved using Equation 3 to develop an expression for vA-after in terms of vB-after. This expression for vA-after can then be substituted into Equation 4. The value of vB-after can then be determined. This is shown below.
From Equation 3:
vA-after = 12 cm/s - 8 cm/s - vB-after
 vA-after = 4 cm/s - vB-after vA-after = 4 cm/s - vB-after
This expression for vA-after in terms of vB-after can now be substituted into equation 4. This is shown below. The subsequent algebraic manipulation is shown as well.
12 cm/s + 4 cm/s - vB-after = - 8 cm/s + vB-after
12 cm/s + 4 cm/s + 8 cm/s - vB-after = + vB-after
24 cm/s = + vB-after + vB-after
24 cm/s = 2 vB-after
vB-after = +12 cm/s
Now that the value of vB-after has been determined, it can be substituted into the original expression for vA-after (Equation 5) in order to determine the numerical value of vA-after. This is shown below.
vA-after = 4 cm/s - vB-after
vA-after = 4 cm/s - 12 cm/s
vA-after = -8.0 cm/s
|
69. A 1.72-kg block of soft wood is suspended by two strings from the ceiling. The wood is free to rotate in pendulum-like fashion when a force is exerted upon it. A 8.50-g bullet is fired into the wood. The bullet enters the wood at 431 m/s and exits the opposite side shortly thereafter. If the wood rises to a height of 13.8 cm, then what is the exit speed of the bullet?
|
Answer: vbullet-after = 98.2 m/s
The difficulty of this problem lies in the fact that information from other units (work and energy) must be combined with the momentum information from this unit to arrive at a solution to the problem. In this scenario there is a collision between a stationary block of wood and a moving bullet. The impulse causes the block of wood to be set into motion and the bullet to slow down. Momentum can be assumed to be conserved. Once set into motion, the block of wood rises in pendulum-like fashion to a given height. Its energy of motion (kinetic energy) is transformed into energy of vertical position (potential energy). The post-collision speed of the wood can be determined using energy conservation equations.
To begin the solution, the final height of the wood is used to determine the post-collision speed of the wood.
KEinitial = PEfinal
0.5 • mwood •vwood2 = mwood • g • hwood
vwood2 = 2 • g • hwood
vwood = SQRT(2 • g • hwood)
vwood = SQRT[2 • (9.8 m/s2) • (0.138 m)]
vwood = SQRT[2.7048 m2/s2]
vwood = 1.6446 m/s
Immediately following the emergence of the bullet from the wood, the wood block is moving with a speed of 1.6446 m/s. Knowing this, momentum conservation can be applied to determine the post-collision speed of the bullet.
mwood • vwood-before + mbullet • vbullet-before = mwood • vwood-after + mbullet • vbullet-after
where vwood-before = 0 m/s; vbullet-before = 431 m/s; vwood-after = 1.6446 m/s; vbullet-after = ???
(1.72 kg) • (0 m/s) + (0.00850 kg) • (431 m/s) = (1.72 kg) • (1.6446 m/s) + (0.00850 kg) • vbullet-after
(To simplify the work, the units will be dropped from the solution in the next several steps. Once a vbullet-after value is found, its units will be in m/s, consistent with the units stated in the above line.)
0 + 3.6635 = 2.8288 + 0.00850 • vbullet-after
0.8347 = 0.00850 • vbullet-after
(0.8347) / (0.00850) = vbullet-after
vbullet-after = 98.205 m/s = ~98.2 m/s
|
70. In a physics lab, the pitching speed of a student is determined by throwing a baseball into a box and observing the box's motion after the catch. A measurement of the the distance the box slides across a rough surface of known coefficient of friction will allow one to determine the pre-impact speed of the pitched ball. If a 0.256-kg ball hits a 3.46-kg box and the ball and box slide a distance of 2.89 meters across a surface with a coefficient of friction of 0.419, then what is the pre-impact speed of the pitched ball?
|
Answer: 70.7 m/s
This is another example of a problem in which information from other units (work and energy or Newton's laws and kinematics) must be combined with the momentum information from this unit to arrive at a solution to the problem. There is a collision between a stationary box and a moving baseball that causes the baseball to slow down and the box to speed up. It is a perfectly inelastic collision with the baseball remaining lodged in the box and the two objects moving together with the same post-collision speed. After the collision occurs, the baseball and box slide a given distance across a rough surface to a final resting position. The coefficient of friction between the box and the surface is given. This latter information (sliding distance and mu value) can be used to determine the post-collision speed of the box and baseball. Once found, momentum conservation can be applied to the collision to determine the pre-collision speed of the baseball.
Work and energy principles will be used to analyze the motion of the box/baseball system sliding to a stop. (Newton's laws and kinematics could just as easily been used). Immediately following the collision, the box/baseball system has kinetic energy. Friction does work upon the box/baseball system to bring to a final resting position, characterized by zero kinetic energy. The motion occurs across a level surface, so there is no potential energy change of the box. The work done by friction is equal to the kinetic energy change of the box/baseball system.
Wfrict = Delta KE
Ffrict • d • cos(Theta) = KEfinal - KEinitial
(mu •Fnorm) • d • cos(180) = 0.5 • m •vfinal2 - 0.5 • m •vinitial2
- (mu • m • g) • d = 0 - 0.5 • m • vinitial2
mu • g • d = 0.5 • vinitial2
2 •mu • g • d = vinitial2
SQRT(2 • mu • g • d) = vinitial
where mu = 0.419; d = 2.89 m; and g = 9.8 m/s2
vinitial = SQRT[2 • (0.419) • (9.8 m/s2 ) • (2.89 m)]
vinitial = SQRT[23.734 m2/s2]
vinitial = 4.8717 m/s
Immediately following the collision, the box/baseball system begins moving with a speed of 4.8717 m/s. Now momentum conservation can be applied to determine the pre-collision speed of the baseball.
mbaseball • vbaseball-before + mBox • vBox-before = mbaseball • vbaseball-after + mBox • vBox- after
(0.256 kg) • vbaseball-before + (3.46 kg) • (0 m/s) = (0.256 kg) • (4.8717 m/s) + (3.46 kg) • (4.8717 m/s)
(To simplify the solution, the units will be dropped from the solution in the next several steps. Once a vbaseball-before value is found, its units will be in m/s, consistent with the units stated in the above line.)
0.256 • vbaseball-before = 1.2472 + 16.8562
0.256 • vbaseball-before = 18.1033
vbaseball-before = (18.1033) / (0.256)
vbaseball-before = 70.7 m/s
|
71. Two ice skaters collide on the ice. A 39.6-kg skater moving South at 6.21 m/s collides with a 52.1-kg skater moving East at 4.33 m/s. The two skaters entangle and move together across the ice. Determine the magnitude and direction of their post-collision velocity.
|
Answer: 3.64 m/s at 42.5 degrees east of south (312.5 degrees)
The difficulty of this problem lies in the fact that the collision occurs between two objects moving at right angles to each other. Thus, vector principles will have to be combined with momentum principles to arrive at a solution to the problem. The same conservation of momentum principle will be used; but when summing the before momentum values of the two objects, the fact that they are at right angles to each means that they will have to be added using the Pythagorean theorem. The collision is perfectly inelastic with the two skaters moving at the same speed after the collision. For communication sake, the 39.6-kg skater will be referred to as skater A and the 52.1-kg skater will be referred to as skater B. A vector diagram will likely assist in the solution of the problem.

The individual momentum of the two skaters is first determined.
pA = mA • vA = (39.6 kg) • (6.21 m/s, South) = 245.916 kg • m/s, South
pB = mB • B = (52.1 kg) • (4.33 m/s, East ) = 225.593 kg • m/s, East
Now the Pythagorean theorem can be used to add these two vectors and thus determine the pre-collision system momentum. The diagram at the right shows the vectors being added in head-to-tail fashion. The resultant is drawn from the tail of the first vector to the head of the last vector. The resultant is the hypotenuse of a right triangle whose sides are the pA and pB vectors.
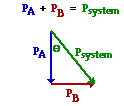 psystem = pA + pB (where pA and pB are right angle vectors) psystem = pA + pB (where pA and pB are right angle vectors)
psystem = SQRT(pA2+ pB2)
psystem = SQRT[(245.916 kg • m/s)2+ (225.593 kg • m/s)2]
psystem = 333.717 kg • m/s
The direction of the this total system momentum vector can be determined by using a trigonometric function. As shown in the diagram above, the angle theta is the angle between the system momentum vector and the vertical. This angle can be determined using either the tangent, cosine or sine function. The tangent function is used below.
tangent(Theta) = opposite side / adjacent side
tangent(Theta) = pB / pA
tangent(Theta) = (225.593 kg • m/s) / (245.916 kg • m/s)
tangent(Theta) = 0.91735
Theta = tan-1 (0.91735)
Theta = 42.532 degrees
Before the collision, the total system momentum is 333.717 kg • m/s in a direction of 42.532 degrees east of south. Since total system momentum is conserved, the after-collision momentum of the system is also 333.717 kg • m/s in a direction of 42.532 degrees east of south. After the collision, the two objects move together as a single unit with the same velocity. The velocity of each object can be found by dividing the total momentum by the total mass.
psystem = msystem • vsystem
vsystem = ( psystem ) / (msystem )
vsystem = (333.717 kg • m/s) / (91.7 kg)
vsystem = 3.64 m/s at 42.5 degrees east of south
|
72. In a physics lab, two carts collide elastically on a level, low-friction track. Cart A has a mass of 1.500 kg and is moving east at 36.5 cm/s. Cart B has a mass of 0.500 kg and is moving West at 42.8 cm/s. Determine the post-collision velocities of the two carts.
|
Answer: vA-after = -3.15 cm/s; vB-after = 76.15 cm/s
This is a perfectly elastic collision in which both momentum and kinetic energy are conserved. The method for solving this problem will be very similar to that used in Problem #68 above. Two equations will be developed using the momentum conservation and kinetic energy conservation principles. One equation will be used to develop an expression for vA in terms of vB. This expression will then be substituted into the second equation in order to solve for vB. The original vA expression can then be used to determine the vA value. The solution is shown below.
The momentum conservation equation can be written as
mA • vA-before + mB • vB-before = mA • vA-after + mB • vB-after
(1.500 kg) • (+36.5 cm/s) + (0.500 kg) • (-42.8 cm/s) = (1.500 kg) • vA-after + (0.500 kg) • vB-after
 33.35 kg • cm/s = (1.500 kg) • vA-after + (0.500 kg) • vB-after 33.35 kg • cm/s = (1.500 kg) • vA-after + (0.500 kg) • vB-after
For elastic collisions, total system kinetic energy is conserved. The kinetic energy conservation equation is written as
0.5 • m • vA-before2 + 0.5 • m • vB-before2 = 0.5 • m • vA-after2 + 0.5 • m • vB-after2
As shown in the book, this equation can be simplified to the form of
vA-before + vA-after = vB-before + vB-after
36.5 cm/s + vA-after = -42.8 cm/s + vB-after
 vA-after = vB-after - 79.3 cm/s vA-after = vB-after - 79.3 cm/s
Now the problem has been reduced to two equations and two unknowns. Such a problem can be solved in numerous ways. Note that equation 2 represents an expression for vA-after in terms of vB-after. This expression for vA-after can then be substituted into Equation 1. The value of vB-after can then be determined. This work is shown below. (To simplify the mathematics, the units will be dropped from the numerical values stated in the solution. When vB-after is solved for, its units will be in cm/s - the same units used for velocity in the above portion of the solution.)
33.35 = (1.500) • (vB-after - 79.3) + (0.500) • vB-after
33.35 = 1.500 • vB-after - 118.95 + 0.500 • vB-after
152.30 = 2.00 • vB-after
vB-after = 76.15 cm/s
Now that the value of vB-after has been determined, it can be substituted into the original expression for vA-after (Equation 2) in order to determine the numerical value of vA-after. This is shown below.
vA-after = vB-after - 79.3 cm/s
vA-after = 76.15 cm/s - 79.3 cm/s
vA-after = -3.15 cm/s
|
[ #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 | #67 | #68 | #69 | #70 | #71 | #72 ]
Navigate to:
Review Session Home - Topic Listing
Momentum and Collisions - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-5 || #6-36 || #37-56 || 57-72
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Momentum and Collisions
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 3 of the series includes topics in Momentum and Collisions.
Visit: MOP the App Home || MOP the App - Part 3