Circular Motion and Gravitation Review
Navigate to:
Review Session Home - Topic Listing
Circular Motion and Gravitation - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-14 || #15-28 || #29-40
Part A: Multiple Choice
1. Which of the following statements are true of an object moving in a circle at a constant speed? Include all that apply.
- The object experiences a force which has a component directed parallel to the direction of motion.
- Inertia causes objects to move in a circle.
- There can be a force pushing outwards on the object as long as the net force in inwards.
- Because the speed is constant, the acceleration is zero.
- The acceleration and the net force vector are directed perpendicular to each other.
- If the net force acting upon the object is suddenly reduced to zero, then the object would suddenly depart from its circular path and travel tangent to the circle.
- The acceleration of the object is directed tangent to the circle.
|
Answer: CF
A is false; if the motion is in a circle at constant speed, the net force is perpendicular to the direction of motion and there is neither a component parallel nor anti-parallel to the direction of motion.)
B is false; it is centripetal force which causes the circular motion. Inertia (which is NOT a force) is merely the tendency of any moving object to continue in its straight-line constant speed path.
C is true; an object which moves in a circle must have a net inward force. There are many instances of individual outwards forces which are exceeded by an individual inward force (e.g., see #5 below).
D is false; acceleration occurs when there is a change in velocity. Since the direction of the velocity vector is changing, there is an acceleration - an inward acceleration.
E is false; the acceleration and net force are always directed in the same direction. In this case, F and a are directed inward; this happens to be perpendicular to the tangential velocity vector.
F is true; if the net force is 0 N, then the moving object will maintain its state of motion. At the instant that Fnet becomes 0 N, the object is moving tangent to the circle.
G is false; the acceleration is directed inwards; only the velocity is directed tangent to the circle.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
For Questions #2-#5, identify the type of force which causes the following bold-faced objects to travel along a circular path.
2. An eraser is tied to a string swung in a horizontal circle.
|
a. gravity
|
b. normal
|
c. tension
|
d. applied
|
|
e. friction
|
f. spring
|
g. electrical
|
h. magnetic
|
3. The moon orbits the earth.
|
a. gravity
|
b. normal
|
c. tension
|
d. applied
|
|
e. friction
|
f. spring
|
g. electrical
|
h. magnetic
|
4. A car makes a sharp right-hand turn along a level roadway.
|
a. gravity
|
b. normal
|
c. tension
|
d. applied
|
|
e. friction
|
f. spring
|
g. electrical
|
h. magnetic
|
5. A roller coaster car passes through a loop. Consider the car at the bottom of the loop.
|
a. gravity
|
b. normal
|
c. tension
|
d. applied
|
|
e. friction
|
f. spring
|
g. electrical
|
h. magnetic
|
|
Answers:
2. C - Tension (A string is attached to the eraser and pulls it towards the center point of the circle.)
3. A - Gravity (All masses attract with a force of gravity. In the case of the moon and the earth, gravity pulls on the moon in a direction which is roughly perpendicular to its path.)
4. E - Friction (Once the wheels are turned, friction can push perpendicular to the wheels' direction, pushing the car towards the center of the circle.)
5. B - Normal (There are two forces at the bottom of the loop; gravity pulls outwards from the center; but the normal force exceeds the magnitude of gravity, pushing inwards with sufficient force to supply the needed centripetal force.)
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
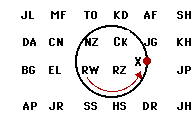 6. A physics teacher ties an eraser to the end of a string and then whirls it in a counter-clockwise circle. If the teacher lets go of the string, then the eraser hits a student (or several students) in the classroom. If the string is let go when the eraser is at point X on the diagram at the right, then which student(s) in the class will the eraser hit? Write the initials in this space: ________________
6. A physics teacher ties an eraser to the end of a string and then whirls it in a counter-clockwise circle. If the teacher lets go of the string, then the eraser hits a student (or several students) in the classroom. If the string is let go when the eraser is at point X on the diagram at the right, then which student(s) in the class will the eraser hit? Write the initials in this space: ________________
|
Answer: JG and AF
Once the centripetal force is no longer present, the eraser will follow its straight-line, inertial path. This path would be directed tangent to the circle and would pass through the locations where JG and AF are sitting. View a reasonably cool animation.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
7. Which of the following statements are true about gravitational force? Identify all that apply.
- The gravitational force only acts between very, very massive objects.
- The gravitational force between an object and the earth is inversely related to the distance between the object's and the earth's center.
- The gravitational force can ALWAYS be accurately calculated by multiplying the object mass by the acceleration of gravity (m•g).
- The gravitational force acting upon an object is the same as the weight of the object.
- The gravitational force between two objects is independent of the mass of the smaller of the two objects.
- If object A gravitationally attracts object B with a force of X Newtons, then object B will also gravitationally attract object A with the same force of X Newtons.
- The doubling of the separation distance (measured from the center) between two objects will halve the gravitational force between the objects.
- It an object is placed two earth-radii above the surface of the earth, then the force of gravitational attraction between the object and the earth will be one-fourth the magnitude as on earth's surface.
- Orbiting astronauts do not experience a force of gravity; this explains why they feel weightless.
|
Answer: BCDF
A is false; gravitational forces are universal (Newton's big idea); they act between any two objects which have mass.
B is true; if the distance is increased, then the force is decreased.
C is true; this is always the case. It is not true however to say that the gravitational force is equal to mass•9.8 m/s/s. The value of g varies with location and so at distances significantly further from the earth's surface, g is reduced and the gravitational force must be computed using a different value of g.
D is true; weight and gravitational force are synonymous.
E is false; gravitational force is dependent upon the product of the two masses. Both masses are important in the computation.
F is true; for every action there is an equal and opposite reaction. This is Newton's third law, an inescapable reality about forces.
G is false; doubling the separation distance will make the force one-fourth the size.
H is false; placing the object at two earth-radii above earth's surface will put 3-earth radii from earth's center. This is equivalent to increasing the separation distance by a factor of 3; this decreases the force by a factor of 9.
I is false; orbiting astronauts must be experiencing the force of gravity. Without this force, there would be no centripetal force and no orbit.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
8. Which of the following statements are true about the acceleration of gravity? Identify all that apply.
- The acceleration of gravity experienced by objects located near to (and far from) from the earth depends upon the mass of the object.
- The acceleration of gravity experienced by objects located near to (and far from) from the earth depends upon the mass of the Earth.
- The acceleration of gravity experienced by objects located near to (and far from) the earth is inversely related to the distance between the center of the object and the center of the earth.
- Increasing the mass of an object will increase the acceleration of gravity experienced by the object.
- Doubling the distance between an object and the earth's center will decrease the acceleration of gravity by a factor of four.
- The acceleration of an orbiting satellite is equal to the acceleration of gravity at that particular location.
- If the mass of the Earth were doubled (without an alteration in its radius), then the acceleration of gravity on its surface would be approximately 20 m/s2.
- If the mass of the Earth were doubled and the radius of the earth were doubled, then the two changes would offset each other and the acceleration of gravity on its surface would still be approximately 10 m/s2.
|
Answer: BCEFG
A is false; check out the equation - g = GMcentral/R2. The value of g does not depend upon the object's mass.
B is true; check out the equation again. The acceleration of gravity created by the earth depends upon the earth's mass.
C is true; check out the equation one more time. The separation distance is located in the denominator of the equation, indicating an inverse relationship.
D is false; like statement A, this statement makes a claim that the acceleration of gravity depends upon the mass of the object. It does not. In the derivation of g from the Universal Gravitation equation, the mass cancels. :)
E is true; g is inversely proportional to the square of the distance; a doubling of the distance means that you must divide the force of gravity value by 4 (22) to obtain the new force of gravity value.
F is true; the acceleration of gravity is the acceleration which is caused by gravity when it is the only force. For an orbiting satellite, gravity is the only force.
G is true; according to the equation, the g value is directly proportional to the mass of the earth. An increase in M results in a proportional increase in g.
H is false; g is approximately 10 m/s/s on earth's surface. Doubling the mass of the earth would increase g to approximately 20 m/s/s. Then doubling the distance from the surface of the earth to its center would decrease g by a factor of 4. The new acceleration of gravity value would be approximately 5 m/s/s. Clearly, these two alterations do not offset each other.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
9. Which of the following statements are true about satellites? Identify all that apply.
- Satellites are falling projectiles.
- All satellites follow circular paths.
- The orbital velocity required of a satellite is dependent upon the mass of the satellite; a more massive satellite would require a greater orbital speed.
- The orbital velocity of a satellite does not depend upon the mass of the planet around which it orbits.
- A high-altitude satellite will require a greater orbital speed than a low-altitude satellite.
- By definition, a geosynchronous satellite orbits the earth in a perfect circle, maintaining the same distance above the surface of the earth.
- Satellites travel faster along their orbital path when they are closest to the earth.
- The acceleration of a satellite varies inversely with its distance from the center of the earth. More distant satellites have smaller accelerations.
|
Answer: AGH
A is true (mostly); satellites are projectiles which are falling towards the Earth without falling into the Earth. They are falling in the sense that (like any projectile), they are dropping below their tangential direction of motion.
B is false; some satellites travel in elliptical and even very elliptical orbits. For instance, the planets orbit the Sun in mildly elliptical paths.
C is false; the equation for the orbital velocity of a satellite is v = SQRT(G•Mcentral/R). The Mcentral is the mass of the central body - the body being orbited by the satellite. As seen in the equation, the orbital velocity is independent of the mass of the satellite.
D is false; the equation for the orbital velocity of a satellite is v = SQRT(G•Mcentral/R). The Mcentral is the mass of the central body - the body being orbited by the satellite. Clearly the orbital velocity depends upon the mass of the planet being orbited.
E is false the equation for the orbital velocity of a satellite is v = SQRT(G•Mcentral/R). The R in the denominator inside the radical is the radius of the orbit. The higher altitude satellites have a greaer radius of orbit. As the R in the denominator increases, the required orbital velocity will decrease.
F is false; by definition, a geosynchronous satellite has synchronized or matched its orbital period to the rotational period of the Earth about its axis - 24 hours.
G is true; this is an idea known since Kepler that is explained by Newton's gravitational law. As a satellite orbits in an elliptical path, the force of gravitation is greatest at the times when it is closest to the Earth; this force causes a greater acceleration and speed of the satellite along these nearest locations of its orbit.
H is true; the acceleration of a satellite is given by the equation g=G•Mcentral/R2 where R is the radius of the orbit. The larger the R value, the smaller the acceleration. This is an inverse square relationship.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
10. Which of the following statements are true about the motion of planets about the sun? Identify all that apply.
- The force of gravity is the only force which acts upon the planets.
- Their trajectories are highly elliptical.
- The planets which are furthest from the sun have the greatest period.
- For any given planet, the speed is greatest when the planet is closest to the sun.
- The velocity vector is directed tangent to the elliptical path.
- The net force vector is at all times directed perpendicular to the velocity vector.
- To keep the planet from escaping the sun's gravitational field, the net force vector is greatest when the planet is furthest from the sun.
|
Answer: ACDE
A is true; gravity is the only force acting upon a planet. Think about it - what other physical push or pull can you identify as acting upon the earth. (People pushing on it and pulling it don't count.)
B is false; their trajectories are indeed elliptical. Yet in most cases, the ellipses are very close to a circle since the eccentricities are very close to 0.
C is true; this is in accord with Kepler's third law: T2/R3 = constant. Expressing this equation another way depicts the direct relationship between T and R: T2 = constant • R3.
D is true; this is Kepler's second law of planetary motion. In order to sweep out equal areas in equal times, a satellite must be moving faster when closest to the earth. See a clever animation.
E is true; at all times during the orbital path, the velocity of the planet is tangent to the path. Since the path has a slightly elliptical nature to it, the force and acceleration vector are not necessarily perpendicular to this velocity vector. The perpendicular orientation of the F and a vectors relative to the v vector is unique to circular motion. An excellent and informative graphic about this can be found online.
F is false; see above explanation and the link to the informative graphic.
G is false; the net force is a gravitational force. Gravitational forces vary inversely with distance. Thus, a planet will experience less force when furthest from the sun. You might really need to view the informative graphic.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
Part B: Short Answer
11. Explain how something can be moving at a constant speed yet be accelerating at the same time.
|
Answer:
The object would have to be traveling in a curved path since it is accelerating. Acceleration is defined as a change in velocity over a change in time. If the speed is staying the same, then the velocity must be changing by altering the direction in which the object is heading. A force is required to do this. See an informative animation and further explanation.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
12. How did Newton come up with the idea that the moon is actually "falling" toward the Earth.
|
Answer:
Newton made the connection between objects falling (accelerating) towards the earth and objects in space which are accelerating towards the earth while they are in circular motion around the earth. Both are being pulled by the earth due to the gravitational force. The moon stays in orbit due to it having the appropriate tangential velocity that keeps it from coming closer to the earth's surface. The moon, however, is still accelerating at the rate any object would have at that distance from the earth. In a sense, the moon is falling around the earth rather than into the earth.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
13. Distinguish between true- and apparent-weightlessness.
|
Answer:
True weightlessness occurs when there is an absence of gravitational force on an object. This is not a likely occurrence since every mass in the universe is attracted to every other mass in the universe with some force of gravity. All objects would experience some degree of gravitational attraction (though it may be considerably small). Apparent weightlessness is the sensation of not experiencing any external contact forces. This occurs when an object is in free-fall. Even though the object may have a large force on it, it wouldn't register on a scale that was in free-fall with it. Astronauts appear this way on the space shuttle.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 ]
14. Describe the apparent weight of a person in an elevator while upward, accelerating downward, and not accelerating.
|
Answer:
When one stands upright on a scale, the scale measures the force of the scale pushing upwards on the body. As such, the scale does not measure one's true weight, but one's apparent weight. An elevator accelerating someone up must not only apply a force to provide the acceleration but also oppose the gravitational force on the person. Therefore, a scale would register a number larger than the gravitational force if the person is accelerating upward. In this case, a person would experience an apparent weight which is greater than usual. Likewise, if the person is accelerating downward the scale reading must be less than the gravitational force since the gravitational force is accelerating them downward. As such, the person's apparent weight is less than what they are accustomed to experiencing. If the elevator is moving at constant velocity or at rest, the scale reading must match the gravitational force in order to have a net force of 0. The apparent weight would be equal to the actual weight of the person.
|
Navigate to:
Review Session Home - Topic Listing
Circular Motion and Gravitation - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-14 || #15-28 || #29-40
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Circular Motion and Gravitation
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 2 of the series includes topics in Circular Motion and Gravitation.
Visit: MOP the App Home || MOP the App - Part 2