The Physics Classroom » Chemistry Tutorial » Stoichiometry » Determining the Excess Amount
Getting your Trinity Audio player ready...

Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.

Lesson 3: Limiting and Excess Reactants

Part c: Determining the Excess Reactant Amount

Part a: Non-Stoichiometric Conditions
Part b: Solving Limiting Reactant Problems
Part c: Determining the Excess Reactant Amount

 

 

The Big Idea

After the limiting reactant is consumed, determine how much of the excess reactant remains using a straightforward two-step process: stoichiometric calculation and subtraction. This lesson walks you through clear worked-out examples to master the method.

 

Limiting and Excess Reactant Problem

On the previous page of Lesson 3, the method of solving a limiting reactant problem was introduced and demonstrated. We did two example problems in which we determined the limiting reactant and the amount of product produced. On this page, we will do the same two problems with an added twist. We will determine the amount of excess reactant remaining after the limiting reactant is used up.
 
 
 

ICE Tables Revisited

Consider the reaction …

N2(g)   +   3 H2(g)   →   2 NH3(g)

The coefficients of the balanced equation indicate that the two reactants react in a 1:3 ratio. Let’s suppose that we start with 2 mol N2 and 8 mol H2 in a reaction container. The fact that the reactants are available in a 1:4 ratio means that there will be a limiting reactant. One reactant gets used up and the other reactant is in excess. There will be some excess reactant remaining when the reaction ends. An ICE Table (presented in Lesson 3a) is a convenient tool for representing this situation.

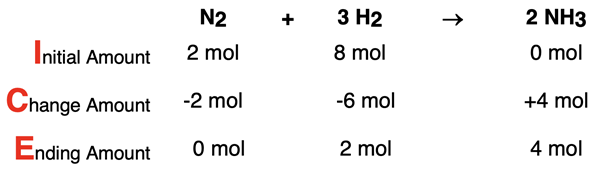
ICE Table for non-limiting reactant problem, showing initial amount, change amount, and ending amount of moles for all species in ammonia synthesis reaction.

 
Since there are 4 parts (moles) of H2 per 1 part N2, the H2 will be in excess. The middle row, Change Amount, is based on the limiting reactant, N2. The N2 will be completely used up and the amount of H2 that reacts with it can be calculated. The 6 mol of H2 that reacts is based on the 2 mol of N2 that reacts. Once the N2 is reacted away, the reaction ceases. At that moment, the H2 amount ceases to change since there is no N2 left for it to react with. So, 2 moles of H2 are in excess or remaining. This is referred to as the amount of excess reactant.
 

 

 

 

Procedure for Determining the Excess Amount

The numerical values in the ICE Table are simple whole numbers, making the computation very easy. It also highlights the two-step procedure.

  1. Mole meme: our mole offering words of encouragement - “Stoichiometry and subtraction. You got this!”Calculate the amount of the excess reactant that will react with all the limiting reactant.
  2. Subtract the amount of the excess reactant that reacts (the Change Amount) from the amount initially available (the Initial Amount) to determine the amount that is left over (the Ending Amount).

Step 1 is a stoichiometry step. Step 2 is a subtraction step.
 
When the amounts of reactants are given in moles, then the stoichiometry calculation is a 1-step, mole-to-mole conversion. If the amounts of reactants are given in grams, then the stoichiometry calculation is a 3-step, gram-to-gram conversion. We discussed both of these types of stoichiometry problems in Lesson 2.
 
Let’s demonstrate this method using a variation of Example 1 and Example 2 from Lesson 3b.



 
 
 

Example 1 - Limiting and Excess Reactant Problem

Given: N2 + 3 H2 → 2 NH3
Suppose 24.1 g of N2 are combined with 6.58 g of H2 in a reaction container.
  1. Which is the limiting and the excess reactant?
  2. How much NH3 is synthesized by the reaction?
  3. How much of the excess reactant remains when the reaction ends?
 
Shows two conversion factor solutions, one for each given reactant mass, for determining the grams of product and identifying the limiting reactant, specific to ammonia synthesis reaction.Parts a and b have already been answered in Lesson 3b. We used the two given amounts of reactant to calculate the amount of NH3 produced. The reactant that produced the least NH3 is the limiting reactant. The amount of product it produced was the amount of NH3 that was synthesized. We determined that N2 was the limiting reactant, H2 was the excess reactant, and 29.3 g of NH3 was produced. The work is shown at the right. A complete discussion can be found in Lesson 3b.
 
Part c of this problem is new to this page. To determine the amount of excess reactant (H2), we will need to do the two steps – the stoichiometry step and the subtraction step. The stoichiometry step involves determining how much H2 will react completely with the 24.1 g N2. This is a three-step, gram-to-gram conversion. We set up our conversions factors first with units but no numbers.
 
Shows the conversion factor set up with unit cancellation for converting from grams of a reactant to grams of a second reactant, specific to ammonia synthesis reaction.
 
Then we insert the numbers into the conversion factors and use our calculator to solve. (If necessary, re-visit Lesson 2c for full details on three-step, gram-to-gram conversions.)
 
Shows the conversion factor solution - arrangement of factors with numbers, units, unit cancellation, and answer - for converting from grams of a reactant to grams of a second reactant, specific to ammonia synthesis reaction.
 
From Step 1, we learn that 5.20 g H2 react with all the N2 that is available. The subtraction subtracting this Change Amount from the Initial Amount.
 
Formula for calculating excess reactant amount as the given amount minus the reacting amount with an example calculation.
 
So, we have determined that 1.38 g H2 are remaining when the reaction is complete.
 
The answers (in red) to the three-part question are:
  1. Which is the limiting and excess reactant?  N2 = limiting rxt, H2 = excess rxt
  2. How much ammonia is synthesized by the reaction?  29.3 g NH3
  3. How much of the excess reactant remains when the reaction ends?  1.38 g H2
 

 
 

Example 2 - Limiting and Excess Reactant Problem

Given:  2 Mg(s)   +   O2(g)   →   2 MgO(s)
An ignition device combines 1.28 g of Mg with 1.02 g of O2.
  1. What is the limiting reactant and the excess reactant?
  2. How much MgO is produced?
  3. How much of the excess reactant remains when the reaction ends?
 
Shows two conversion factor solutions, one for each given reactant mass, for determining the grams of product and identifying the limiting reactant, specific to MgO synthesis reaction.Once again, parts a and b have already been answered in Lesson 3b. We used the two given amounts of reactant to calculate the amount of MgO produced. The reactant that produced the least product was the limiting reactant. The amount of product it produced was the amount of MgO that was produced. We determined that Mg was the limiting reactant, O2 was the excess reactant, and 2.12 g of MgO was produced. The work is shown at the right. A complete discussion can be found in Lesson 3b.
 
Part c of this problem is new to this page. To determine the amount of excess reactant (O2), we will need to do the two steps – the stoichiometry step and the subtraction step. The stoichiometry step involves determining how much O2 will react completely with the 1.28 g Mg. This is a three-step, gram-to-gram conversion. We set up our conversions factors first with units but no numbers.
 
Shows the conversion factor set up with unit cancellation for converting from grams of a reactant to grams of a second reactant, specific to MgO synthesis reaction.
 
Then we insert the numbers into the conversion factors and use our calculator to solve. (If necessary, re-visit Lesson 2c for full details on three-step, gram-to-gram conversions.)
 
Shows the conversion factor solution - arrangement of factors with numbers, units, unit cancellation, and answer - for converting from grams of a reactant to grams of a second reactant, specific to MgO synthesis reaction.
 
From Step 1, we learn that 0.842 g O2 react with all the Mg that is available. The subtraction involves subtracting this Change Amount from the Initial Amount.
 
Formula for calculating excess reactant amount as the given amount minus the reacting amount with an example calculation.
 
So, we have determined that 0.18 g O2 are remaining when the reaction is complete.
 
The answers (in red) to the three-part question are:
  1. Which is the limiting and excess reactant?  Mg = limiting rxt, O2 = excess rxt
  2. How much MgO is produced?  2.12 g MgO
  3. How much of the excess reactant remains when the reaction ends?  0.18 g O2
 
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 
  • Explore our Limiting Reactant Simulation. Investigate how the ratio of available moles of reactants results in leftover reactants and affects the amount of product produced. Eight different reactions can be studied.
  • CalcPad - Stoichiometry Problem Sets: Problem Sets ST13 through ST15 include several limiting and excess reactant problems. Answer the question and receive immediate feedback and opportunities to correct your errors. Awesome follow up!
  • The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
  • Download our Study Card on Limiting and Excess Reactant Problems. Save it to a safe location and use it as a review tool.
 
 
 

Check Your Understanding of Limiting and Excess Reactant Problems

Use the following questions to assess your skill at solving a limiting and excess reactant problem. Tap the Check Answer buttons when ready.
 
1. Consider the synthesis of titanium (III) oxide from its elements.
 
4 Ti (s)   +   3 O2(g)   →   2 Ti2O3(s)
 
Suppose 2.88 g of Ti are combined with 1.05 g O2 in a reaction container.
  1. Identify the limiting reactant and the excess reactant.
  2. Determine the amount of Ti2O3 produced.
  3. Determine the amount of the excess reactant that remains when the reaction ends.

Check Answer



 
 
2. Consider the reaction …
 
2 H2(g)   +   O2(g)   →   2 H2O(l)
 
Suppose 7.98 grams H2 are combined with 49.1 g O2 in a reaction container.
  1. Identify the limiting reactant and the excess reactant.
  2. Determine the amount of H2O produced.
  3. Determine the amount of the excess reactant that remains when the reaction ends.

 
​

Check Answer