Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
 There are three mathematical quantities that will be of primary interest to us as we analyze the motion of objects in circles. These three quantities are speed, acceleration and force. The speed of an object moving in a circle is given by the following equation.
There are three mathematical quantities that will be of primary interest to us as we analyze the motion of objects in circles. These three quantities are speed, acceleration and force. The speed of an object moving in a circle is given by the following equation.

The acceleration of an object moving in a circle can be determined by either two of the following equations.

The equation on the right (above) is derived from the equation on the left by the substitution of the expression for speed.
The net force (Fnet) acting upon an object moving in circular motion is directed inwards. While there may by more than one force acting upon the object, the vector sum of all of them should add up to the net force. In general, the inward force is larger than the outward force (if any) such that the outward force cancels and the unbalanced force is in the direction of the center of the circle. The net force is related to the acceleration of the object (as is always the case) and is thus given by the following three equations:
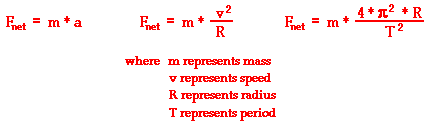
The equations in the middle (above) and on the right (above) are derived from the equation on the left by the substitution of the expressions for acceleration.
This set of circular motion equations can be used in two ways:
These two ways are illustrated below.
Equations as a Guide to Thinking
An equation expresses a mathematical relationship between the quantities present in that equation. For instance, the equation for Newton's second law identifies how acceleration is related to the net force and the mass of an object.

The relationship expressed by the equation is that the acceleration of an object is directly proportional to the net force acting upon it. In other words, the bigger the net force value is, the bigger that the acceleration value will be. As net force increases, the acceleration increases. In fact, if the net force were increased by a factor of 2, the equation would predict that the acceleration would increase by a factor of 2. Similarly, if the net force were decreased by a factor of 2, the equation would predict that the acceleration would decrease by a factor of 2.
Newton's second law equation also reveals the relationship between acceleration and mass. According to the equation, the acceleration of an object is inversely proportional to mass of the object. In other words, the bigger the mass value is, the smaller that the acceleration value will be. As mass increases, the acceleration decreases. In fact, if the mass were increased by a factor of 2, the equation would predict that the acceleration would decrease by a factor of 2. Similarly, if the mass were decreased by a factor of 2, the equation would predict that the acceleration would increase by a factor of 2.
As mentioned previously, equations allow for predictions to be made about the affect of an alteration of one quantity on a second quantity. Since the Newton's second law equation shows three quantities, each raised to the first power, the predictive ability of the equation is rather straightforward. The predictive ability of an equation becomes more complicated when one of the quantities included in the equation is raised to a power. For instance, consider the following equation relating the net force (Fnet) to the speed (v) of an object moving in uniform circular motion.

This equation shows that the net force required for an object to move in a circle is directly proportional to the square of the speed of the object. For a constant mass and radius, the Fnet is proportional to the speed2.

The factor by which the net force is altered is the square of the factor by which the speed is altered. Subsequently, if the speed of the object is doubled, the net force required for that object's circular motion is quadrupled. And if the speed of the object is halved (decreased by a factor of 2), the net force required is decreased by a factor of 4.
Equations as a Recipe for Problem-Solving
The mathematical equations presented above for the motion of objects in circles can be used to solve circular motion problems in which an unknown quantity must be determined. The process of solving a circular motion problem is much like any other problem in physics class. The process involves a careful reading of the problem, the identification of the known and required information in variable form, the selection of the relevant equation(s), substitution of known values into the equation, and finally algebraic manipulation of the equation to determine the answer. Consider the application of this process to the following two circular motion problems.
|
Sample Problem #1
A 900-kg car moving at 10 m/s takes a turn around a circle with a radius of 25.0 m. Determine the acceleration and the net force acting upon the car.
|
The solution of this problem begins with the identification of the known and requested information.
|
Known Information:
m = 900 kg
v = 10.0 m/s
R = 25.0 m
|
Requested Information:
a = ????
Fnet = ????
|
To determine the acceleration of the car, use the equation a = v2 / R. The solution is as follows:
a = v2 / R
a = (10.0 m/s)2 / (25.0 m)
a = (100 m2/s2) / (25.0 m)
a = 4 m/s2
To determine the net force acting upon the car, use the equation Fnet = m•a. The solution is as follows.
Fnet = m • a
Fnet = (900 kg) • (4 m/s2)
Fnet = 3600 N
|
Sample Problem #2
A 95-kg halfback makes a turn on the football field. The halfback sweeps out a path that is a portion of a circle with a radius of 12-meters. The halfback makes a quarter of a turn around the circle in 2.1 seconds. Determine the speed, acceleration and net force acting upon the halfback.
|
The solution of this problem begins with the identification of the known and requested information.
|
Known Information:
m = 95.0 kg
R = 12.0 m
Traveled 1/4-th of the circumference in 2.1 s
|
Requested Information:
v = ????
a = ????
Fnet = ????
|
To determine the speed of the halfback, use the equation v = d / t where the d is one-fourth of the circumference and the time is 2.1 s. The solution is as follows:
v = d / t
v = (0.25 • 2 • pi • R) / t
v = (0.25 • 2 • 3.14 • 12.0 m) / (2.1 s)
v = 8.97 m/s
To determine the acceleration of the halfback, use the equation a = v2 / R. The solution is as follows:
a = v2 / R
a = (8.97 m/s)2 / (12.0 m)
a = (80.5 m2/s2) / (12.0 m)
a = 6.71 m/s2
To determine the net force acting upon the halfback, use the equation Fnet = m•a. The solution is as follows.
Fnet = m*a
Fnet = (95.0 kg)*(6.71 m/s2)
Fnet = 637 N
In Lesson 2 of this unit, circular motion principles and the above mathematical equations will be combined to explain and analyze a variety of real-world motion scenarios including amusement park rides and circular-type motions in athletics.
We Would Like to Suggest ...

Sometimes it isn't enough to just read about it. You have to interact with it! And that's exactly what you do when you use one of The Physics Classroom's Interactives. We would like to suggest that you combine the reading of this page with the use of either our
Uniform Circular Motion Interactive or our
Horizontal Circle Simulation. You can find them in the Physics Interactives section of our website. The
Uniform Circular Motion Interactive allows a learner to interactively explore the relationship between velocity, acceleration, and force for an object moving in a circle. Our
Horizontal Circle Simulation simulates the motion of three different objects moving in a horizontal circle while analyzing the effect that modifcations in a variable can have upon the motion.
Check Your Understanding
1. Anna Litical is practicing a centripetal force demonstration at home. She fills a bucket with water, ties it to a strong rope, and spins it in a circle. Anna spins the bucket when it is half-full of water and when it is quarter-full of water. In which case is more force required to spin the bucket in a circle? Explain using an equation as a "guide to thinking."
2. A Lincoln Continental and a Yugo are making a turn. The Lincoln is four times more massive than the Yugo. If they make the turn at the same speed, then how do the centripetal forces acting upon the two cars compare. Explain.
3. The Cajun Cliffhanger at Great America is a ride in which occupants line the perimeter of a cylinder and spin in a circle at a high rate of turning. When the cylinder begins spinning very rapidly, the floor is removed from under the riders' feet. What affect does a doubling in speed have upon the centripetal force? Explain.
4. Determine the centripetal force acting upon a 40-kg child who makes 10 revolutions around the Cliffhanger in 29.3 seconds. The radius of the barrel is 2.90 meters.