One-Dimensional Kinematics Review
Part A: Multiple TRUE/FALSE
1. Which of the following statements about vectors and scalars are TRUE? List all that apply.
- A vector is a large quantity and a scalar is a small quantity.
- A scalar quantity has a magnitude and a vector quantity does not.
- A vector quantity is described with a direction and a scalar is not.
- Scalar quantities are path dependent quantities and vector quantities are not.
- A scalar quantity depends only upon the initial and final values of the quantity; this is not the case for vector quantities.
- The quantity 20 m/s, north is a speed and as such is a scalar quantity.
- The quantity 9.8 m/s/s is an acceleration value and as such is a vector quantity.
2. Which of the following statements about distance and/or displacement are TRUE? List all that apply.
- Distance is a vector quantity and displacement is a scalar quantity.
- A person makes a round-trip journey, finishing where she started. The displacement for the trip is 0 and the distance is some nonzero value.
- A person starts at position A and finishes at position B. The distance for the trip is the length of the segment measured from A to B.
- If a person walks in a straight line and never changes direction, then the distance and the displacement will have exactly the same magnitude.
- The phrase "20 mi, northwest" likely describes the distance for a motion.
- The phrase "20 m, west" likely describes the displacement for a motion.
- The diagram below depicts the path of a person walking to and fro from position A to B to C to D. The distance for this motion is 100 yds.
- For the same diagram below, the displacement is 50 yds.
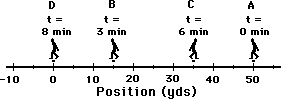
3. Which of the following statements about velocity and/or speed are TRUE? List all that apply.
- Velocity is a vector quantity and speed is a scalar quantity.
- Both speed and velocity refer to how fast an object is moving.
- Person X moves from location A to location B in 5 seconds. Person Y moves between the same two locations in 10 seconds. Person Y is moving with twice the speed as person X.
- The velocity of an object refers to the rate at which the object's position changes.
- For any given motion, it is possible that an object could move very fast yet have an abnormally small velocity.
- The phrase "30 mi/hr, west" likely refers to a scalar quantity.
- The average velocity of an object on a round-trip journey would be 0.
- The direction of the velocity vector is dependent upon two factors: the direction the object is moving and whether the object is speeding up or slowing down.
- The diagram below depicts the path of a person walking to and fro from position A to B to C to D. The entire motion takes 8 minutes. The average speed for this motion is approximately 11.3 yds/min.
- For the same diagram below, the average velocity for this motion is 0 yds/min.
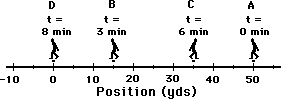
4. Which of the following statements about acceleration are TRUE? List all that apply.
- Acceleration is a vector quantity.
- Accelerating objects MUST be changing their speed.
- Accelerating objects MUST be changing their velocity.
- Acceleration units include the following; m/s2, mi/hr/sec, cm/s2, km/hr/m.
- The direction of the acceleration vector is dependent upon two factors: the direction the object is moving and whether the object is speeding up or slowing down.
- An object which is slowing down has an acceleration.
- An object which is moving at constant speed in a circle has an acceleration.
- Acceleration is the rate at which the velocity changes.
- An object that is accelerating is moving fast.
- An object that is accelerating will eventually (if given enough time) be moving fast.
- An object that is moving rightward has a rightward acceleration.
- An object that is moving rightward and speeding up has a rightward acceleration.
- An object that is moving upwards and slowing down has an upwards acceleration.
5. Which of the following statements about position-time graphs are TRUE? List all that apply.
- Position-time graphs cannot be used to represent the motion of objects with accelerated motion.
- The slope on a position-time graph is representative of the acceleration of the object.
- A straight, diagonal line on a position-time graph is representative of an object with a constant velocity.
- If an object is at rest, then the position-time graph will be a horizontal line located on the time-axis.
- Accelerated objects are represented on position-time graphs by curved lines.
- An object with a positive velocity will be represented on a position-time graph by a line with a positive slope.
- An object with a negative velocity will be represented on a position-time graph by a line with a negative slope.
- An object with a positive acceleration will be represented on a position-time graph by a line which curves upwards.
- An object with a negative acceleration will be represented on a position-time graph by a line which curves downwards.
6. Which of the following statements about velocity-time graphs are TRUE? List all that apply.
- The slope on a velocity-time graph is representative of the acceleration of the object.
- The area on a velocity -time graph is representative of the change in position of the object.
- An accelerated object's motion will be represented by a curved line on a velocity-time graph.
- Objects with positive acceleration will be represented by upwardly-curved lines on a velocity-time graph.
- If an object is at rest, then the velocity-time graph will be a line with zero slope.
- A line with zero slope on a velocity-time graph will be representative of an object which is at rest.
- A line with a negative slope on a velocity-time graph is representative of an object with negative velocity.
- If an object changes its direction, then the line on the velocity-time graph will have a changing slope.
- An object which is slowing down is represented by a line on a velocity-time graph which is moving in the downward direction.
7. Which of the following statements about free fall and the acceleration of gravity are TRUE? List all that apply.
- An object that is free-falling is acted upon by the force of gravity alone.
- A falling skydiver which has reached terminal velocity is considered to be in a state of free fall.
- A ball is thrown upwards and is rising towards its peak. As it rises upwards, it is NOT considered to be in a state of free fall.
- An object in free fall experiences an acceleration which is independent of the mass of the object.
- A ball is thrown upwards, rises to its peak and eventually falls back to the original height. As the ball rises, its acceleration is upwards; as it falls, its acceleration is downwards.
- A ball is thrown upwards, rises to its peak and eventually falls back to the original height. The speed at which it is launched equals the speed at which it lands. (Assume negligible air resistance.)
- A very massive object will free fall at the same rate of acceleration as a less massive object.
- The value of g on Earth is approximately 9.8 m/s2.
- The symbol g stands for the force of gravity.
Part B: Multiple Choice
8. If an object has an acceleration of 0 m/s2, then one can be sure that the object is not ____.
|
a. moving
|
b. changing position
|
c. changing velocity
|
9. If car A passes car B, then car A must be ____.
- accelerating.
- accelerating at a greater rate than car B.
- moving faster than car B and accelerating more than car B.
- moving faster than car B, but not necessarily accelerating.
10. Which one of the following is NOT consistent with a car which is accelerating?
- A car is moving with an increasing speed.
- A car is moving with a decreasing speed.
- A car is moving with a high speed.
- A car is changing direction.
11. A fullback is running down the football field in a straight line. He starts at the 0-yard line at 0 seconds. At 1 second, he is on the 10-yard line; at 2 seconds, he is on the 20-yard line; at 3 seconds, he is on the 30-yard line; and at 4 seconds, he is on the 40-yard line. This is evidence that
- he is accelerating
- he is covering a greater distance in each consecutive second.
- he is moving with a constant speed (on average).
12. A fullback is running down the football field in a straight line. He starts at the 0-yard line at 0 seconds. At 1 second, he is on the 10-yard line; at 2 seconds, he is on the 20-yard line; at 3 seconds, he is on the 30-yard line; and at 4 seconds, he is on the 40-yard line. What is the player's acceleration?
13. Olympic gold medalist Michael Johnson runs one time around the track - 400 meters - in 38 seconds. What is his displacement? ___________ What is his average velocity? ___________
14. If an object is moving eastward and slowing down, then the direction of its velocity vector is ____.
|
a. eastward
|
b. westward
|
c. neither
|
d. not enough info to tell
|
15. If an object is moving eastward and slowing down, then the direction of its acceleration vector is ____.
|
a. eastward
|
b. westward
|
c. neither
|
d. not enough info to tell
|
16. Which one of the following quantities is NOT a vector?
|
a. 10 mi/hr, east
|
b. 10 mi/hr/sec, west
|
c. 35 m/s, north
|
d. 20 m/s
|
17. Which one of the following quantities is NOT a speed?
|
a. 10 mi/hr
|
b. 10 mi/hr/sec
|
c. 35 m/s
|
d. 20 m/s
|
18. Which one of the following statements is NOT true of a free-falling object? An object in a state of free fall ____.
- falls with a constant speed of -10 m/s.
- falls with a acceleration of -10 m/s/s.
- falls under the sole influence of gravity.
- falls with downward acceleration which has a constant magnitude.
19. The average speed of an object which moves 10 kilometers (km) in 30 minutes is ____.
|
a. 10 km/hr
|
b. 20 km/hr
|
c. 30 km/hr
|
d. more than 30 km/hr
|
20. What is the acceleration of a car that maintains a constant velocity of 55 mi/hr for 10.0 seconds?
|
a. 0
|
b. 5.5 mi /hr/s
|
c. 5.5 mi /s/s
|
d. 550 mi/hr/s
|
21. As an object freely falls, its ____.
|
a. speed increases
|
b. acceleration increases
|
|
c. both of these
|
d. none of these
|
22. A speedometer is placed upon a free-falling object in order to measure its instantaneous speed during the course of its fall. Its speed reading (neglecting air resistance) would increase each second by ____.
|
a. about 5 m/s
|
b. about 10 m/s
|
c. about 15 m/s
|
| d. a variable amount |
e. depends on its initial speed. |
|
23. Ten seconds after being dropped from rest, a free-falling object will be moving with a speed of ____.
|
a. about 10 m/s.
|
b. about 50 m/s.
|
c. about 100 m/s.
|
d. more than 100 m/s.
|
24. A baseball pitcher delivers a fast ball. During the throw, the speed of the ball increases from 0 to 30.0 m/s over a time of 0.100 seconds. The average acceleration of the baseball is ____ m/s2.
|
a. 3.00
|
b. 30.0
|
c. 300.
|
d. 3000
|
e. none of these
|
25. On takeoff, a rocket accelerates from rest at a rate of 50.0 m/s2 for exactly 1 minute. The rocket's speed after this minute of steady acceleration will be ____ m/s.
|
a. 50.0
|
b. 500.
|
c. 3.00 x 103
|
d. 3.60 x 103
|
e. none of these
|
26. When a rock is dropped, it will accelerate downward at a rate of 9.8 m/s2. If the same rock is thrown downward (instead of being dropped from rest), it acceleration will be ____. (Ignore air resistance effects.)
|
a. less than 9.8 m/s2
|
b. 9.8 m/s2
|
c. more than 9.8 m/s2
|
27. Consider drops of water that leak from a dripping faucet at a constant rate. As the drops fall they ____.
|
a. get closer together
|
b. get farther apart
|
|
|
c. remain at a relatively fixed distance from one another
|
28. Renatta Oyle is again found driving her '86 Yugo down Lake Avenue, leaving the following trail of oil drops on the pavement.

If her car is moving from right to left, then ...
- her velocity has a rightward direction and her acceleration has a rightward direction.
- her velocity has a rightward direction and her acceleration has a leftward direction.
- her velocity has a leftward direction and her acceleration has a rightward direction.
- her velocity has a leftward direction and her acceleration has a leftward direction.
Part C: Diagramming
29. On the diagrams below, construct a dot diagram representing the motion of an object with a ... .
- constant rightward velocity
- rightward velocity and a rightward acceleration
- rightward velocity and a leftward acceleration
- rightward velocity, first slow and constant, and then accelerating to a high speed
- rightward velocity, first decelerating from a high speed to a rest position, then maintaining the rest position, and finally accelerating at a lower rate than the initial deceleration.
30. On a dot diagram, how does the motion of an object moving to the right and slowing down differ from an object moving to the left and speeding up? Explain.
Part D: Kinematic Graphing
31. On the position-time graph below, sketch a plot representing the motion of an object which is ... . Label each line with the corresponding letter (e.g., "a", "b", "c", etc.)
-
at rest.
-
moving in the positive direction with constant speed
-
moving in the negative direction and speeding up
-
moving in the positive direction and slowing down
-
moving in the positive direction at a constant speed (slow) and then later fast at constant speed
-
moving with a negative velocity and a negative acceleration
-
moving with a negative velocity and a positive acceleration

32. On the velocity-time graph below, sketch a plot representing the motion of an object which is ... . Label each line with the corresponding letter (e.g., "a", "b", "c", etc.)
-
at rest
-
moving in the positive direction at constant speed
-
moving in the negative direction from slow to fast
-
moving in the negative direction from fast to slow
-
moving with a positive velocity and a positive acceleration
-
moving with a positive velocity and a negative acceleration
-
moving with a positive velocity at constant speed and then decelerating to a rest position
-
moving in the positive direction while slowing down, changing directions and moving in the negative directions while speeding up
33. Consider the position-time plots below. Sketch the shape of the corresponding velocity-time graphs.
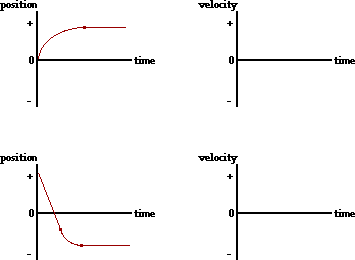
34. Consider the velocity-time plots below. Sketch the shape of the corresponding position-time graphs.
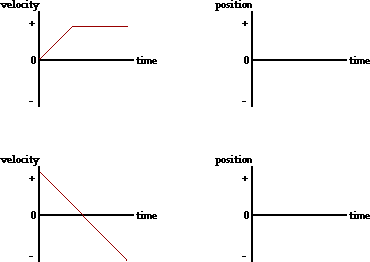
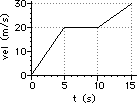
The velocity-time graph below depicts the motion of an automobile as it moves through Glenview during rush hour traffic. Use the graph to answer questions #35 - #39.
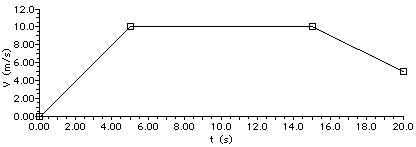
35. Determine the displacement of the automobile during the following intervals of time. PSYW
|
t = 0.0 s - 5.0 s
|
t = 5.0 s - 15.0 s
|
t = 15.0 s - 20.0 s
|
|
|
|
|
36. Determine the velocity of the automobile at the following instant(s) in time.
|
t = 3.0 s
|
t = 8.0 s
|
t = 17.0 s
|
|
|
|
|
37. Determine the acceleration of the automobile during the following intervals of time.
|
t = 0.0 s - 5.0 s
|
t = 5.0 s - 15.0 s
|
t = 15.0 s - 20.0 s
|
|
|
|
|
38. Using complete sentences and the language of physics, describe the motion of the automobile during the entire 20.0 seconds. Explicitly describe any changes in speed or direction which might occur; identify intervals of time for which the automobile is at rest, the automobile is moving with constant speed, or the automobile is accelerating.
39. Supposing the automobile has an oil leak, demonstrate your understanding of its motion by drawing an oil drop diagram for the 20.0 seconds of motion. Divide the diagram into three distinct time intervals (0.0 - 5.0 seconds, 5.0 - 15.0 seconds, 15.0 - 20.0 seconds).
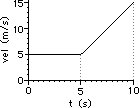
40. For the plots below, determine the velocity of the object ... .
|
a. from 0.0 - 5.0 seconds
|
b. from 5.0 - 10.0 seconds
|
c. at 13.0 seconds
|
|
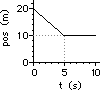
|
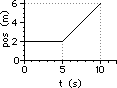
|
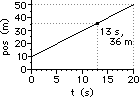
|
41. For the plots below, determine the acceleration of the object ... .
|
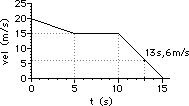
a. from 0.0 - 5.0 seconds
|
b. from 5.0 - 10.0 seconds
|
c. at 13.0 seconds
|
|
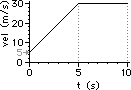
|
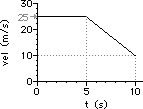
|
|
42. For the plots below, determine the displacement of the object ... .
|
a. from 0.0 - 5.0 seconds
|
b. from 5.0 - 10.0 seconds
|
c. from 0.0 - 15.0 seconds
|
|
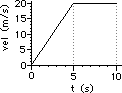
|
|
|
Part E: Computational Problems
43. Determine the acceleration (in m/s2) of an object which ... .
-
moves in a straight line with a constant speed of 20.0 m/s for 12.0 seconds
-
changes its velocity from 12.1 m/s to 23.5 m/s in 7.81 seconds
-
changes its velocity from 0.0 mi/hr to 60.0 mi/hr in 4.20 seconds
-
accelerates from 33.4 m/s to 18.9 m/s over a distance of 109 m
44. Determine the magnitude of the displacement (in meters) of an object which ... .
-
moves from Hither to Yon (with an average speed of 28.0 m/s) and then back to Hither (with an average speed of 28.0 m/s) if both the forward and the return trip take 46 minutes each.
-
moves at a constant speed of 8.30 m/s in a straight line for 15.0 seconds.
-
decelerates at a rate of -4.35 m/s/s from a speed of 38.1 m/s to a speed of 17.6 m/s
-
accelerates from rest at a rate of 3.67 m/s2 for 12.1 seconds
-
is moving at 12.2 m/s and then accelerates at a rate of +1.88 m/s2 for 17.0 seconds
45. The hare is sleeping at a location that is 1200 m from the finish line. The tortoise passes him at a steady speed of 5.0 cm/s. If the hare finally wakes up 6.5 hours later, then what minimum acceleration (assumed constant) must he have in order to pass the tortoise before the finish line.
46. A Gold Car moving at 12.0 m/s passes a Green Car while the Green Car is at rest at a stoplight. The Green Car immediately accelerates at a rate of +1.80 m/s/s for 11.0 seconds seconds and then maintains a constant speed. After how much time (relative to the initial starting time) must the Green Car drive before catching up with the Gold Car.
47. Ima Rilla Saari is cruising at 28.0 m/s down Lake Avenue and through the forest preserve. She notices a deer jump into the road at a location 62.0 m in front of her. Ima first reacts to the event, then slams on her brakes and decelerates at -8.10 m/s2, and ultimately stops a picometer in front of the frozen deer. What is Ima's reaction time? (i.e., how long did it take Ima to react to the event prior to decelerating?)
48. A two-stage rocket accelerates from rest at +3.57 m/s/s for 6.82 seconds. It then accelerates at +2.98 m/s/s for another 5.90 seconds. After the second stage, it enters into a state of free fall. Determine:
-
the maximum speed
-
the maximum altitude
-
the height of the rocket after 20.0 seconds
-
the total time the rocket is in the air (assuming it is launched from the ground)
49. In a 200.0-m relay race (each leg of the race is 50.0 m long), one swimmer has a 0.450 second lead and is swimming at a constant speed of 3.90 m/s towards the opposite end of the pool. What minimum speed must the second swimmer have in order to catch up with the first swimmer by the end of the pool?
50. A drag racer accelerates from rest at an average rate of +13.2 m/s2 for a distance of 100. m. The driver coasts for 0.500 seconds and then uses the brakes and parachute to decelerate until the end of the track. If the total length of the track is 180. m, what minimum deceleration rate must the racer have in order to stop prior to the end of the track?
Navigate to:
Review Session Home - Topic Listing
1D Kinematics - Home ||
Printable Version ||
Questions and Links
Answers to Questions:
#1-7 ||
#8-#28 ||
#29-#42 ||
#43-#50
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Kinematics
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 1 of the series includes Kinematic Concepts and Kinematic Graphing.
Visit: MOP the App Home || MOP the App - Part 1