Mechanics: Work, Energy and Power
Work, Energy and Power: Problem Set Overview
There are 20 ready-to-use problem sets on the topic of Work, Energy, and Power. The problems target your ability to use equations related to work and power, to calculate the kinetic, potential and total mechanical energy, and to use the work-energy relationship in order to determine the final speed, stopping distance or final height of an object.
Work
Work results when a force acts upon an object to cause a displacement (or a motion) or, in some instances, to hinder a motion of a moving object. Three variables are of importance in this definition - force, displacement, and the extent to which the force causes or hinders the displacement. Each of these three variables find their way into the equation for work. That equation is:
Work = Force • Displacement • Cosine(theta)
W = F • d • cos(Θ)
Since the standard metric unit of force is the Newton and the standard meteric unit of displacement is the meter, then the standard metric unit of work is a Newton•meter, defined as a Joule and abbreviated with a J.
The most complicated part of the work equation and work calculations is the meaning of the angle theta (Θ) in the above equation. The angle is not just any stated angle in the problem; it is the angle between the F and the d vectors. In solving work problems, one must always be aware of this definition - theta is the angle between the force and the displacement which it causes. If the force is in the same direction as the displacement, then the angle is 0 degrees. If the force is in the opposite direction as the displacement, then the angle is 180 degrees. If the force is up and the displacement is to the right, then the angle is 90 degrees. This is summarized in the graphic below.
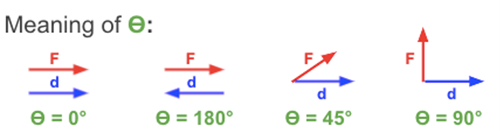
Power
Power is defined as the rate at which work is done upon an object. Like all rate quantities, power is a time-based quantity. Power is related to how fast a job is done. Two identical jobs or tasks can be done at different rates - one slowly or and one rapidly. The work is the same in each case (since they are identical jobs) but the power is different. The equation for power shows the importance of time:
Power = Work / time
P = W / t
The unit for standard metric work is the Joule and the standard metric unit for time is the second, so the standard metric unit for power is a Joule / second, defined as a Watt and abbreviated W. Special attention should be taken so as not to confuse the unit Watt, abbreviated W, with the quantity work, also abbreviated by the letter W.
Combining the equations for power and work can lead to a second equation for power. Power is W/t and work is F•d•cos(theta). Substituting the expression for work into the power equation yields P = F•d•cos(theta)/t. If this equation is re-written as
P = F • cos(Θ) • (d/t)
one notices a simplification which could be made. The d/t ratio is the speed value for a constant speed motion or the average speed for an accelerated motion. Thus, the equation can be re-written as
P = F • v • cos(Θ)
where v is the constant speed or the average speed value. A few of the problems in these problem sets will utilize this derived equation for power.
Mechanical, Kinetic and Potential Energies
There are two forms of mechanical energy - potential energy and kinetic energy.
Potential energy is the stored energy of position. In this set of problems, we will be most concerned with the stored energy due to the vertical position of an object within Earth's gravitational field. Such energy is known as the gravitational potential energy (PEgrav) and is calculated using the equation
PEgrav = m•g•h
where m is the mass of the object (with standard units of kilograms), g is the gravitational field constant (9.8 N/kg) and h is the height of the object (with standard units of meters) above some arbitraily defined zero level (such as the ground or the top of a lab table in a physics room).
Potential energy can also be stored in a mass-spring system. This is known as elastic potential energy (PEelastic). As a spring is stretched some distance x from its equilibrium position, potential energy is stored in the spring-mass system. This type of potential energy is calculated using the equation
PEelastic = 1/2• k • x2
where x is the amount of stretch from the equilibrium position and k is the spring constant of the spring.
Kinetic energy is defined as the energy possessed by an object due to its motion. An object must be moving to possess kinetic energy. The amount of kinetic energy (KE) possessed by a moving object is dependent upon mass and speed. The equation for kinetic energy is
KE = 0.5 • m • v2
where m is the mass of the object (with standard units of kilograms) and v is the speed of the object (with standard units of m/s).
The total mechanical energy possessed by an object is the sum of its kinetic and potential energies.
Work-Energy Connection
There is a relationship between work and total mechanical energy. The relationship is best expressed by the equation
TMEi + Wnc = TMEf
In words, this equation says that the initial amount of total mechanical energy (TMEi) of a system is altered by the work which is done to it by non-conservative forces (Wnc). The final amount of total mechanical energy (TMEf) possessed by the system is equivalent to the initial amount of energy (TMEi) plus the total work done by these non-conservative forces (Wnc).
The mechanical energy possessed by a system is the sum of the kinetic energy and the potential energy. Thus the above equation can be re-arranged to the form of
KEi + PEi + Wnc = KEf + PEf
0.5 • m • vi2 + m • g • hi + F • d • cos(Θ) = 0.5 • m • vf2 + m • g • hf
The work done to a system by non-conservative forces (Wnc) can be described as either positive work or negative work. Positive work is done on a system when the force doing the work acts in the direction of the motion of the object. Negative work is done when the force doing the work opposes the motion of the object. When a positive value for work is substituted into the work-energy equation above, the final amount of energy will be greater than the initial amount of energy; the system is said to have gained mechanical energy. When a negative value for work is substituted into the work-energy equation above, the final amount of energy will be less than the initial amount of energy; the system is said to have lost mechanical energy. There are occasions in which the only forces doing work are conservative forces (sometimes referred to as internal forces). Typically, such conservative forces include gravitational forces, elastic or spring forces, electrical forces and magnetic forces. When the only forces doing work are conservative forces, then the Wnc term in the equation above is zero. In such instances, the system is said to have conserved its mechanical energy.
The proper approach to a work-energy problem involves carefully reading the problem description and substituting values from it into the work-energy equation listed above. Inferences about certain terms will have to be made based on a conceptual understanding of kinetic and potential energy. For instance, if the object is initially on the ground, then it can be inferred that the PEi is 0 and that term can be canceled from the work-energy equation. In other instances, the height of the object is the same in the initial state as in the final state, so the PEi and the PEf terms are the same. As such, they can be mathematically canceled from each side of the equation. In other instances, the speed is constant during the motion, so the KEi and KEf terms are the same and can thus be mathematically canceled from each side of the equation. Finally, there are instances in which the KE and or the PE terms are not stated; rather, the mass (m), speed (v), and height (h) is given. In such instances, the KE and PE terms can be determined using their respective equations. Make it your habit from the beginning to simply start with the work and energy equation, to cancel terms which are zero or unchanging, to substitute values of energy and work into the equation and to solve for the stated unknown.
Habits of an Effective Problem-Solver
An effective problem solver by habit approaches a physics problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits which they share in common. These habits are described briefly here. An effective problem-solver...
- ...reads the problem carefully and develops a mental picture of the physical situation. If needed, they sketch a simple diagram of the physical situation to help visualize it.
- ...identifies the known and unknown quantities in an organized manner, often times recording them on the diagram itself. They equate given values to the symbols used to represent the corresponding quantity (e.g., m = 1.50 kg, vi = 2.68 m/s, F = 4.98 N, t = 0.133 s, vf = ???).
- ...plots a strategy for solving for the unknown quantity. The strategy will typically center saround the use of physics equations and is heavily dependent upon an understanding of physics principles.
- ...identifies the appropriate formula(s) to use, often times writing them down. Where needed, they perform the needed conversion of quantities into the proper unit.
- ...performs substitutions and algebraic manipulations in order to solve for the unknown quantity.
Read more...
Additional Readings/Study Aids:
The following pages from The Physics Classroom tutorial may serve to be useful in assisting you in the understanding of the concepts and mathematics associated with these problems.
Watch a Video
We have developed and continue to develop Video Tutorials on introductory physics topics. You can find these videos on our YouTube channel. We have an entire Playlist on the topic of Work and Energy.