Hold down the T key for 3 seconds to activate the audio accessibility mode, at which point you can click the K key to pause and resume audio. Useful for the Check Your Understanding and See Answers.
Does a Spinning Object Have Kinetic Energy?
Back in Lesson 1 of Work, Energy and Power, we described kinetic energy as energy of motion. Since a spinning object is moving, it must have kinetic energy, right?! Not so fast. Our equation for calculating kinetic energy was KE = ½ m v2, where v was the linear speed at which the object (specifically the center of mass of the object) moves. Since an object that is rotating about its center is not translating (that is, its center of mass is not moving), how could it have kinetic energy?
Let’s answer this question by thinking of the uniform disk that is spinning around its center. It’s true that every point on the disk (except the axis itself) is actually moving with some velocity. So, each point on the disk must have a little kinetic energy. If we add up the little KE of each point on the disk, we’d get the total kinetic energy of the spinning disk. Doing this calculation is challenging, however, since each point mass is traveling with a different velocity. What is true, however, is that each point mass on the disk is traveling with the same angular velocity.

We’ve seen so far in this chapter that each translational quantity has a corresponding rotational quantity. We’ve seen, for example, that a rotating object’s moment of inertia is the rotational counterpart to mass, and that the angular velocity is the rotational counterpart to linear velocity. So, is there a rotational counterpart to kinetic energy? Indeed, there is. That’s what this section is all about.

The answer to our questions is "yes," a spinning object has rotational kinetic energy. Rotational kinetic energy is still energy of motion, and it is still measured in Joules. The equation KErot = ½ I ω2 is just a convenient way to determine the kinetic energy of a rotating object, whereas the translational kinetic energy equation, KEtrans = ½ m v2, helps us determine the kinetic energy of objects moving in a line. Before we move on, let’s consider an example in which we calculate the rotational kinetic energy of a spinning object.
Example 1: The Flywheel
Problem: Delivery trucks that start and stop frequently often get poor gas mileage. Such trucks in Europe have made use of energy stored in a rotating flywheel (a uniform disk) to store rotational kinetic energy needed for the trucks’ frequent starts. Prior to their shift, electric motors get flywheels spinning up to 600 rad/s. If the mass of the flywheel is 500 kg and its radius is 1.0 m, what is the flywheel’s...
(A) Rotational Inertia?
(B) Rotational Kinetic Energy?

Solution: (A) To find the rotational inertia of the flywheel, we’ll use the moment of inertia equation for a disk. Doing so, we get I = 250 kg·m2.

(B) To find the flywheel’s kinetic energy, we use the rotational kinetic energy equation to get KE = 4.5 x 107 Joules.

This is a large amount of energy--perhaps enough to keep a truck making deliveries for several hours. It is a clever solution, but it adds significant mass and size to the truck in order to contain this spinning flywheel. While batteries in electric trucks have a comparable mass, they can be more compact. As such, battery-powered electric delivery trucks are becoming more and more common today.
Translational Kinetic Energy and Rotational Kinetic Energy
Can a moving object have both translational kinetic energy and rotational kinetic energy at the same time? When we introduced rolling back in Lesson 1, we wrote the equation
Pure Translation + Pure Rotation = Rolling
This equation holds true for kinetic energies as well. In other words, a rolling ball can be thought of as having both translational kinetic energy (its center of mass is moving linearly) and rotational kinetic energy (it is rotating about its center of mass). So, for a rolling object,

This works as long as we consider KEtrans as the pure translational kinetic energy of the center of mass and KErot as the pure rotational kinetic energy about the center of mass. Let’s consider a rolling object to see how we can apply this equation.
Example 2: Kinetic Energy of a Rolling Bowling Ball
Problem: Hope Forastrike enjoys bowling in her spare time. Hope rolls a bowling ball down a lane at the bowling alley. The length of a lane is 18.3 meters, and it takes 3.05 seconds for the ball to travel this length. If the bowling ball has a mass of 7.0 kg and a radius of 0.11 m, what is the ball’s total kinetic energy?
Solution: We’ll begin this problem by finding the linear speed of the ball. Since the ball traveled 18.3 meters in 3.05 seconds, v = d/t = 18.3 m/3.05 s = 6.0 m/s. Recall from Lesson 1 that this linear speed is equal to the speed of the ball’s center of mass. Since the ball is rolling (without slipping), let’s also determine the magnitude of the ball’s angular velocity. Using the link equation, v = r ω, we find ω = v / r = (6.0 m/s) / (0.11 m/rad) = 54.5 rad/s. We’ll also need to determine the bowling ball’s moment of inertia about its center of mass. ICM = ½ M R2 = ½ (7.0kg)·(0.11 m)2 = 0.042 kg·m2. Finally, we’ll put these ideas together to determine the total kinetic energy of the ball to be 188 J.
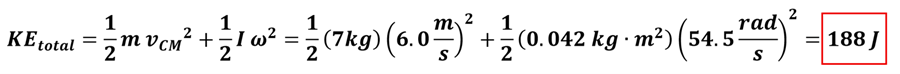
We can consider an object to have both types of kinetic energy only when the object is both translating and rotating simultaneously. We do need to be careful that we don’t double-count an object’s kinetic energy by including both terms when both are not present. Here is an example to illustrate this point.
Example 3: Who's Right?
Problem: Spinna Ball was twirling a small marble (which can be treated as a point mass) on the end of a string as Ida Betterduck determined the time it takes for the marble to travel around the circle once. Spinna claims, "This marble has translational kinetic energy since the ball has a tangential speed as it travels." Ida argues, "No, it has rotational kinetic energy since the marble spins around the big circle." Each student supports their claim. Who is correct?
Solution: Both are actually correct. Here is a case where either perspective gives us the same results. What we don’t want to do in this situation, however, is double-count the kinetic energy. As an analogy, a penny has two sides—heads and tails. Both provide a different perspective of the penny, but it is still just one cent. Similarly, both approaches in this example will determine the same kinetic energy.
Check Your Understanding
Use the following questions to assess your understanding. Tap the Check Answer buttons when ready.
1: A disk and a ring have the same radius R and the same mass M. They are both caused to rotate with the same angular velocity ω about a fixed axis through their center. Which has the greater rotational kinetic energy?

2: A communication satellite can be approximated as a solid disk of mass M = 1100 kg and radius R = 1.5 m. If it is set to spin at 2.0 revolutions/sec,
(A) What is its angular velocity in radians/second?
(B) How much rotational kinetic energy does the spinning satellite have?
3: The rotor of a helicopter spins three blades (which can be approximated as a rod pivoted about their ends). Each blade has a mass of 130 kg and a length of 5.0 m.
(A) What is the rotational inertia of this three-blade system?
(B) How much rotational kinetic energy does this three-blade system have when spinning at 1200 rad/s?

4: Assume the Earth is a uniform solid sphere (radius = 6.38 x 106 m, and mass = 5.97 x 1024 kg). Calculate...
(A) Its rotational Inertia
(B) Its rotational kinetic energy
(C) How long (in years) could it supply 1.2 kW of power to each of the 8 billion people on Earth if this rotational kinetic energy could somehow be harvest for our use?
Looking for additional practice? Check out the CalcPad (RD7) for additional practice problems.
Figure 1 Image generated using some MS Word Iconography.
Figure 2 Hand icon in picture borrowed from Wikimedia Commons (From Gan Khoon Lay) https://commons.wikimedia.org/wiki/File:Icon-angry-hand-4230419.svg under license Creative Commons
Figure 3 Borrowed from Wikimedia Commons https://commons.wikimedia.org/wiki/File:COMMUNICATIONS_SATELLITE_-_NARA_-_17472478.jpg
Figure 4 Earth icon in picture Borrowed from Wikimedia Commons https://commons.wikimedia.org/wiki/File:Earth_icon_2.png