Momentum and Collisions Review
Navigate to:
Review Session Home - Topic Listing
Momentum and Collisions - Home || Printable Version || Questions with Links
Answers to Questions: All || #1-5 || #6-36 || #37-56 || 57-72
Part A: Multiple-Multiple Choice
1. Which of the following statements are true about momentum?
- Momentum is a vector quantity.
- The standard unit on momentum is the Joule.
- An object with mass will have momentum.
- An object which is moving at a constant speed has momentum.
- An object can be traveling eastward and slowing down; its momentum is westward.
- Momentum is a conserved quantity; the momentum of an object is never changed.
- The momentum of an object varies directly with the speed of the object.
- Two objects of different mass are moving at the same speed; the more massive object will have the greatest momentum.
- A less massive object can never have more momentum than a more massive object.
- Two identical objects are moving in opposite directions at the same speed. The forward moving object will have the greatest momentum.
- An object with a changing speed will have a changing momentum.
|
Answer: ADGHK
a. TRUE - Momentum is a vector quantity. Like all vector quantities, the momentum of an object is not fully described until the direction of the momentum is identified. Momentum, like other vector quantities, is subject to the rules of vector operations.
b. FALSE - The Joule is the unit of work and energy. The kg m/s is the standard unit of momentum.
c. FALSE - An object has momentum if it is moving. Having mass gives an object inertia. When that inertia is in motion, the object has momentum.
d. TRUE - This is true. However, one should be quick to note that the object does not have to have a constant speed in order to have momentum.
e. FALSE - The direction of an object's momentum vector is in the direction that the object is moving. If an object is traveling eastward, then it has an eastward momentum. If the object is slowing down, its momentum is still eastward. Only its acceleration would be westward.
f. FALSE - To say that momentum is a conserved quantity is to say that if a system of objects can be considered to be isolated from the impact of net external forces, then the total momentum of that system is conserved. In the absence of external forces, the total momentum of a system is not altered by a collision. However, the momentum of an individual object is altered as momentum is transferred between colliding objects.
g. TRUE - Momentum is calculated as the product of mass and velocity. As the speed of an object increases, so does its velocity. As a result, an increasing speed leads to an increasing momentum - a direct relationship.
h. TRUE - For the same speed (and thus velocity), a more massive object has a greater product of mass and velocity; it therefore has more momentum.
i. FALSE - A less massive object would have a greater momentum owing to a velocity which is greater than that of the more massive object. Momentum depends upon two quantities * mass and velocity. Both are equally important.
j. FALSE - When comparing the size of two momentum vectors, the direction is insignificant. The direction of any vector would never enter into a size comparison.
k. TRUE - Objects with a changing speed also have a changing velocity. As such, an object with a changing speed also has a changing momentum.
|
2. Which of the following are true about the relationship between momentum end energy?
- Momentum is a form of energy.
- If an object has momentum, then it must also have mechanical energy.
- If an object does not have momentum, then it definitely does not have mechanical energy either.
- Object A has more momentum than object B. Therefore, object A will also have more kinetic energy.
- Two objects of varying mass have the same momentum. The least massive of the two objects will have the greatest kinetic energy.
|
Answer: BE
a. FALSE - No. Momentum is momentum and energy is energy. Momentum is NOT a form of energy; it is simply a quantity which proves to be useful in the analysis of situations involving forces and impulses.
b. TRUE - If an object has momentum, then it is moving. If it is moving, then it has kinetic energy. And if an object has kinetic energy, then it definitely has mechanical energy.
c. FALSE - If an object does NOT have momentum, then it definitely does NOT have kinetic energy. However, it could have some potential energy and thus have mechanical energy.
d. FALSE - Consider Object A with a mass of 10 kg and a velocity of 3 m/s. And consider Object B with a mass of 2 kg and a velocity of 10 m/s. Object A clearly has more momentum. However, Object B has the greatest kinetic energy. The kinetic energy of A is 45 J and the kinetic energy of B is 100 J.
e. TRUE - When comparing the momentum of two objects to each other, one must consider both mass and velocity; both are of equal importance when determining the momentum value of an object. When comparing the kinetic energy of two objects, the velocity of an object is of double importance. So if two objects of different mass have the same momentum, then the object with the least mass has a greater velocity. This greater velocity will tip the scales in favor of the least massive object when a kinetic energy comparison is made.
|
3. Which of the following statements are true about impulse?
- Impulse is a force.
- Impulse is a vector quantity.
- An object which is traveling east would experience a westward directed impulse in a collision.
- Objects involved in collisions encounter impulses.
- The Newton is the unit for impulse.
- The kg•m/s is equivalent to the units on impulse.
- An object which experiences a net impulse will definitely experience a momentum change.
- In a collision, the net impulse experienced by an object is equal to its momentum change.
- A force of 100 N acting for 0.1 seconds would provide an equivalent impulse as a force of 5 N acting for 2.0 seconds.
|
Answer: BDFGHI
a. FALSE - Impulse is NOT a force. Impulse is a quantity which depends upon both force and time to change the momentum of an object. Impulse is a force acting over time.
b. TRUE - Impulse is a vector quantity Like momentum, impulse is not fully described unless a direction is associated with it.
c. FALSE - An object which is traveling east could encounter a collision from the side, from behind (by a faster-moving object) or from the front. The direction of the impulse is dependent upon the direction of the force exerted upon the object. In each of these scenarios, the direction of the force would be different.
d. TRUE - In a collision, there is a collision force which endures for some amount of time. The combination of force and time is what is referred to as an impulse.
e. FALSE - The Newton is the unit of force. The standard metric unit of impulse is the N•s.
f. TRUE - The N•s is the unit of momentum. The Newton can be written as a kg•m/s^2. When substituted into the N•s expression, the result is the kg m/s.
g. TRUE - In a collision, there is a collision force which endures for some amount of time to cause an impulse. This impulse acts upon the object to change its velocity and thus its momentum.
h. TRUE - Yes!!! This is the impulse-momentum change theorem. The impulse encountered by an object in a collision causes and is equal to the momentum change experienced by that object.
i. TRUE - A force of 100 N for 0.10 s results in an impulse of 10 N•s. This 10 N•s impulse is equivalent to the impulse created by a force of 5 N for 2.0 seconds.
|
4. Which of the following statements are true about collisions?
- Two colliding objects will exert equal forces upon each other even if their mass is significantly different.
- During a collision, an object always encounters an impulse and a change in momentum.
- During a collision, the impulse which an object experiences is equal to its velocity change.
- The velocity change of two respective objects involved in a collision will always be equal.
- While individual objects may change their velocity during a collision, the overall or total velocity of the colliding objects is conserved.
- In a collision, the two colliding objects could have different acceleration values.
- In a collision between two objects of identical mass, the acceleration values could be different.
- Total momentum is always conserved between any two objects involved in a collision.
- When a moving object collides with a stationary object of identical mass, the stationary object encounters the greater collision force.
- When a moving object collides with a stationary object of identical mass, the stationary object encounters the greater momentum change.
- A moving object collides with a stationary object; the stationary object has significantly less mass. The stationary object encounters the greater collision force.
- A moving object collides with a stationary object; the stationary object has significantly less mass. The stationary object encounters the greater momentum change.
|
Answer: ABF
a. TRUE - In any collision between two objects, the colliding objects exert equal and opposite force upon each other. This is simply Newton's law of action-reaction.
b. TRUE - In a collision, there is a collision force which endures for some amount of time to cause an impulse. This impulse acts upon the object to change its momentum.
c. FALSE - The impulse encountered by an object is equal to mass multiplied by velocity change - that is, momentum change.
d. FALSE - Two colliding objects will only experience the same velocity change if they have the same mass and the collision occurs in an isolated system. However, their momentum changes will be equal if the system is isolated from external forces.
e. FALSE - This statement is mistaking the term velocity for momentum. It is momentum which is conserved by an isolated system of two or more objects.
f. TRUE - Two colliding objects will exert equal forces upon each other. If the objects have different masses, then these equal forces will produce different accelerations.
g. FALSE - It the colliding objects have different masses, the equal force which they exert upon each other will lead to different acceleration values for the two objects.
h. FALSE - Total momentum is conserved only if the collision can be considered isolated from the influence of net external forces.
i. FALSE - In any collision, the colliding objects exert equal and opposite forces upon each other as the result of the collision interaction. There are no exceptions to this rule.
j. FALSE - In any collision, the colliding objects will experience equal (and opposite) momentum changes, provided that the collision occurs in an isolated system.
k. FALSE - In any collision, the colliding objects exert equal and opposite forces upon each other as the result of the collision interaction. There are no exceptions to this rule.
l. FALSE - In any collision, the colliding objects will experience equal (and opposite) momentum changes, provided that the collision occurs in an isolated system.
|
5. Which of the following statements are true about elastic and inelastic collisions?
- Perfectly elastic and perfectly inelastic collisions are the two opposite extremes along a continuum; where a particular collision lies along the continuum is dependent upon the amount kinetic energy which is conserved by the two objects.
- Most collisions tend to be partially to completely elastic.
- Momentum is conserved in an elastic collision but not in an inelastic collision.
- The kinetic energy of an object remains constant during an elastic collision.
- Elastic collisions occur when the collision force is a non-contact force.
- Most collisions are not inelastic because the collision forces cause energy of motion to be transformed into sound, light and thermal energy (to name a few).
- A ball is dropped from rest and collides with the ground. The higher that the ball rises upon collision with the ground, the more elastic that the collision is.
- A moving air track glider collides with a second stationary glider of identical mass. The first glider loses all of its kinetic energy during the collision as the second glider is set in motion with the same original speed as the first glider. Since the first glider lost all of its kinetic energy, this is a perfectly inelastic collision.
- The collision between a tennis ball and a tennis racket tends to be more elastic in nature than a collision between a halfback and linebacker in football.
|
Answer: AEFGI
a. TRUE - A perfectly elastic collision is a collision in which the total kinetic energy of the system of colliding objects is conserved. Such collisions are typically characterized by bouncing or repelling from a distance. In a perfectly inelastic collision (as it is sometimes called), the two colliding objects stick together and move as a single unit after the collision. Such collisions are characterized by large losses in the kinetic energy of the system.
b. FALSE - Few collisions are completely elastic. A completely elastic collision occurs only when the collision force is a non-contact force. Most collisions are either perfectly inelastic or partially inelastic.
c. FALSE - Momentum can be conserved in both elastic and inelastic collisions provided that the system of colliding objects is isolated from the influence of net external forces. It is kinetic energy that is conserved in a perfectly elastic collision.
d. FALSE - In a perfectly elastic collision, in an individual object may gain or lose kinetic energy. It is the system of colliding objects which conserves kinetic energy.
e. TRUE - Kinetic energy is lost from a system of colliding objects because the collision transforms kinetic energy into other forms of energy - sound, heat and light energy. When the colliding objects don't really collide in the usual sense (that is when the collision force is a non-contact force), the system of colliding objects does not lose its kinetic energy. Sound is only produced when atoms of one object make contact with atoms of another object. And objects only warm up (converting mechanical energy into thermal energy) when their surfaces meet and atoms at those surfaces are set into vibrational motion or some kind of motion.
f. TRUE - See above statement.
g. TRUE - If large amounts of kinetic energy are conserved when a ball collides with the ground, then the post-collision velocity is high compared to the pre-collision velocity. The ball will thus rise to a height which is nearer to its initial height.
h. FALSE - This is a perfectly elastic collision. Before the collision, all the kinetic energy is in the first glider. After the collision, the first glider has no kinetic energy; yet the second glider has the same mass and velocity as the first glider. As such, the second glider has the kinetic energy which the first glider once had.
i. TRUE - There is significant bounce in the collision between a tennis racket and tennis ball. There is typically little bounce in the collision between a halfback and a linebacker (though there are certainly exceptions to this one). Thus, the ball-racket collision tends to be more elastic.
|
Part B: Multiple Choice
6. Which of the following objects have momentum? Include all that apply.
a. An electron is orbiting the nucleus of an atom.
b. A UPS truck is stopped in front of the school building.
c. A Yugo (a compact car) is moving with a constant speed.
d. A small flea walking with constant speed across Fido's back.
e. The high school building rests in the middle of town.
|
Answer: A, C, and D
Momentum can be thought of as mass in motion. An object has momentum if it has its mass in motion. It matters not whether the object is of large mass or small mass, moving with constant speed or accelerating; if the object is MOVING, then it has momentum!
|
7. A truck driving along a highway road has a large quantity of momentum. If it moves at the same speed but has twice as much mass, its momentum is ________________.
|
a. zero
|
b. quadrupled
|
c. doubled
|
d. unchanged
|
|
Answer: C
Momentum is directly related to the mass of the object. So for the same speed, a doubling of mass leads to a doubling of momentum.
|
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 | #67 | #68 | #69 | #70 | #71 | #72 ]
8. TRUE or FALSE:
A ball is dropped from the same height upon various flat surfaces. For the same collision time, impulses are smaller when the most bouncing take place.
|
Answer: B
Since being dropped from the same height, the balls will be moving with the same pre-collision velocity (assuming negligible air resistance). Upon collision with the ground, the velocity will have to be reduced to zero - that is, the ball will cease moving downwards. This decrease in velocity constitutes the first portion of the velocity change. If the ball bounces, then there is an additional velocity change sending the ball back upwards opposite the original direction. Thus, for the same collision time, bouncing involves a greater velocity change, a greater momentum change, and therefore a greater impulse.
|
9. Consider a karate expert. During a talent show, she executes a swift blow to a cement block and breaks it with her bare hand. During the collision between her hand and the block, the ___.
- time of impact on both the block and the expert's hand is the same
- force on both the block and the expert's hand have the same magnitude
- impulse on both the block and the expert's hand have the same magnitude
- all of the above.
- none of the above.
|
Answer: D
In any collision, there are always four quantities which are the same for both objects involved in the collision. Each object experiences the same force (Newton's third law) for the same amount of time, leading to the same impulse, and subsequently the same momentum change. Only the acceleration and the velocity change can differ for the two colliding objects. The lower mass object always receives the greater velocity change and acceleration.
|
10. It is NOT possible for a rocket to accelerate in outer space because ____. List all that apply.
- there is no air in space
- there is no friction in space
- there is no gravity in outer space
- ... nonsense! Rockets do accelerate in outer space.
|
Answer: D
Rockets accelerate in outer space by means of Newton's third law of motion. It does not matter that there is no air outside of the rocket. Rockets produce their own gas by burning fuels. The combustion of rocket fuels produces gaseous products. The rocket's thrusters push these gases backwards (or rightwards, or leftwards, or ...) and the gases push the rocket forwards (or leftwards, or rightwards, or ...). Thus, rockets indeed can and do accelerate in outer space.
|
11. In order to catch a ball, a baseball player naturally moves his or her hand backward in the direction of the ball's motion once the ball contacts the hand. This habit causes the force of impact on the players hand to be reduced in size principally because ___.
- the resulting impact velocity is lessened
- the momentum change is decreased
- the time of impact is increased
- the time of impact is decreased
- none of these
|
Answer: C
Increasing the time over which the ball's momentum is brought to 0 will decrease the force required to stop it. Suppose a ball is coming at you with 100-units of momentum. An impulse of 100-units would be required to stop the ball. Regardless of how the impulse is accomplished (big F, little t or little F, big t), there must be 100-units of it. Imparting such an impulse over a long time results in a small force.
|
12. Suppose that Paul D. Trigger fires a bullet from a gun. The speed of the bullet leaving the muzzle will be the same as the speed of the recoiling gun ____.
- because momentum is conserved
- because velocity is conserved
- because both velocity and momentum are conserved
- only if the mass of the bullet equals the mass of the gun
- none of these
|
Answer: D
In any collision or explosion involving two objects, the momentum change for each object is the same. So both the bullet and the gun encounter the same momentum change. The momentum change is simply the mass multiplied by the velocity change. Thus, the velocity change would only be the same if their masses were the same. Otherwise, the smaller-mass object receives a greater velocity change.
|
13. Suppose that you're driving down the highway and a moth crashes into the windshield of your car. Which undergoes the greater change is momentum?
|
a. the moth
|
b. your car
|
c. both the same
|
|
Answer: C
In any collision, there are always four quantities which are the same for both objects involved in the collision. Each object experiences the same force (Newton's third law) for the same amount of time, leading to the same impulse, and subsequently the same momentum change. Only the acceleration and the velocity change can differ for the two objects. The object with the least mass always receives the greatest velocity change and acceleration.
|
14. Suppose that you're driving down the highway and a moth crashes into the windshield of your car. Which undergoes the greater force?
|
a. the moth
|
b. your car
|
c. both the same
|
|
Answer: C
In any collision, there are always four quantities which are the same for both objects involved in the collision. Each object experiences the same force (Newton's third law) for the same amount of time, leading to the same impulse, and subsequently the same momentum change. Only the acceleration and the velocity change can differ for the two objects. The object with the least mass always receives the greatest velocity change and acceleration.
|
15. Suppose that you're driving down the highway and a moth crashes into the windshield of your car. Which undergoes the greater impulse?
|
a. the moth
|
b. your car
|
c. both the same
|
|
Answer: C
In any collision, there are always four quantities which are the same for both objects involved in the collision. Each object experiences the same force (Newton's third law) for the same amount of time, leading to the same impulse, and subsequently the same momentum change. Only the acceleration and the velocity change can differ for the two objects. The object with the least mass always receives the greatest velocity change and acceleration.
|
16. Suppose that you're driving down the highway and a moth crashes into the windshield of your car. Which undergoes the greater acceleration?
|
a. the moth
|
b. your car
|
c. both the same
|
|
Answer: A
In any collision, there are always four quantities which are the same for both objects involved in the collision. Each object experiences the same force (Newton's third law) for the same amount of time, leading to the same impulse, and subsequently the same momentum change. Only the acceleration and the velocity change can differ for the two objects. The object with the least mass always receives the greatest velocity change and acceleration.
|
|
17. Three boxes, X, Y, and Z, are at rest on a table as shown in the diagram at the right. The weight of each box is indicated in the diagram. The net or unbalanced force acting on box Y is _____.
|
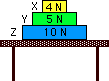
|
|
a. 4 N down
|
b. 5 N down
|
c. 5 N up
|
d. 10 N up
|
e. zero
|
|
|
Answer: E
If an object is at rest, then all the forces acting upon the object must be zero. The net force on any one of the boxes is 0 Newtons. Subsequently, in each case, the support force (which we have called the "normal force throughout this course) acting upwards on any of the boxes must be equal to the force of gravity on that box (i.e., the weight) plus the amount of load exerted from above (which would be equivalent to the weight of the other boxes located above the box). So for box Y, the support force acting upward would be equal to 9 N while the net force is still 0 Newtons. And for box Z, the support force is 19 N, sufficient to balance the 10-N gravitational force plus the 9-N of force resulting from the other two boxes bearing down on it.
|
18. In a physics experiment, two equal-mass carts roll towards each other on a level, low-friction track. One cart rolls rightward at 2 m/s and the other cart rolls leftward at 1 m/s. After the carts collide, they couple (attach together) and roll together with a speed of _____________. Ignore resistive forces.
|
a. 0.5 m/s
|
b. 0.33 m/s
|
c. 0.67 m/s
|
d. 1.0 m/s
|
e. none of these
|
|
Answer: A
Use 1 kg as the mass of the carts (or any number you wish) and then set the expression for initial total momentum equal to the expression for the final total momentum:
(1 kg)*(2) + (1 kg) *(-1) = (1 kg) *v + (1 kg) *v
Now solve for v using the proper algebraic steps.
(2 kg•m/s) - (1 kg•m/s) = (2 kg) v
1 kg•m/s = (2 kg)v
(1 kg•m/s) / (2 kg) = v
0.5 m/s = v
|
19. A physics cart rolls along a low-friction track with considerable momentum. If it rolls at the same speed but has twice as much mass, its momentum is ____.
|
a. zero
|
b. four times as large
|
c. twice as large
|
d. unchanged
|
|
Answer: C
The momentum of an object is calculated as the product of mass and velocity. Thus, the momentum is directly proportional to the mass of the object. If the mass of an object is somehow doubled, the momentum is doubled as well.
|
20. The firing of a bullet by a rifle causes the rifle to recoil backwards. The speed of the rifle's recoil is smaller than the bullet's forward speed because the ___.
|
a. force against the rifle is relatively small
|
b. speed is mainly concentrated in the bullet
|
|
c. rifle has lots of mass
|
d. momentum of the rifle is unchanged
|
|
e. none of these
|
|
|
Answer: C
Please don't answer A (for it will make Newton roll over in his grave and he's getting quite tired of that). Perhaps you've heard that "for every action, there is an equal and opposite ...". Choice B is invalid; speed is not something that becomes concentrated or squeezed into an object. Choice D is invalid; ask anyone who's fired a rifle if the rifle is set into motion by the firing of the bullet. (Of course, since it is set in motion, its momentum is not unchanged.) Because of the large mass of the rifle, the acceleration and the recoil speed of the rifle is small.
|
21. Two objects, A and B, have the same size and shape. Object A is twice as massive as B. The objects are simultaneously dropped from a high window on a tall building. (Neglect the effect air resistance.) The objects will reach the ground at the same time but object A will have a greater ___. Choose all that apply.
|
a. speed
|
b. acceleration
|
c. momentum
|
|
d. none of the above quantities will be greater
|
|
Answer: C
The two objects free-fall at the same rate of acceleration, thus giving them the same speed when they hit the ground. The heavier object however has more momentum since momentum takes into account both the speed and the mass of the object (p=m*v).
|
22. Cars are equipped with padded dashboards. In collisions, the padded dashboards would be safer than non-padded ones because they ____. List all that apply.
|
a. increase the impact time
|
b. decrease an occupant's impulse
|
|
c. decrease the impact force
|
d. none of the above
|
|
Answer: AC
Both A and C are correct. Padded dashboard serve to increase the time over which the momentum of a passenger is reduced to zero. With this increase in time, there is a decrease in force (big T, little f).
The impulse acting upon the passenger is not changed. The passenger still must have his/her mass slowed down from the pre-impact velocity to zero velocity. This means the velocity change is the same whether the collision occurs with a padded dashboard, an air bag or a glass windshield. Since the velocity change is independent of the collision time, the momentum change and the required impulse are also independent of the collision time.
|
23. A 4 kg object has a momentum of 12 kg•m/s. The object's speed is ___ m/s.
|
a. 3
|
b. 4
|
c. 12
|
d. 48
|
e. none of these.
|
|
Answer: A
This is a relatively simple plug-and-chug into the equation p=m*v with m=4 kg and p=12 kg•m/s.
|
24. A wad of chewed bubble gum is moving with 1 unit of momentum when it collides with a heavy box that is initially at rest. The gum sticks to the box and both are set in motion with a combined momentum that is ___.
|
a. less than 1 unit
|
b. 1 unit
|
c. more than 1 unit
|
d. not enough information
|
|
Answer: B
Before the collision, the total system momentum is 1 unit - all due to the motion of the wad of gum. Since momentum must be conserved, the total momentum of the box and gum after the collision must also be 1 unit.
|
|
25. A relatively large force acting for a relatively long amount of time on a relatively small mass will produce a relatively ______. List all that apply.
|
a. small velocity change
|
b. large velocity change
|
|
c. small momentum change
|
d. small acceleration
|
|
Answer: B
A large force acting upon a small mass will result in a large acceleration (a=F/m) and subsequently a large velocity change (Delta v = a*t). This rules out choices A and D. A large force and for a long time will result in a large impulse and therefore a large momentum change. This rules out choice C.
|
26. Consider the concepts of work and energy (presuming you have already studied it) and those of impuse and momentum. Force and time is related to momentum change in the same manner as force and displacement pertains to ___________.
|
a. impulse
|
b. work
|
c. energy change
|
d. velocity
|
e. none of these.
|
|
Answer: C
A force multiplied by a time gives an impulse which will cause (and be equal to) a momentum change. In the same manner, a force multiplied by a displacement gives work which will cause (and be equal to) an energy change. Take the time to reread those two sentences because it relates two big concepts.
|
27. A 5-N force is applied to a 3-kg ball to change its velocity from +9 m/s to +3 m/s. This impulse causes the momentum change of the ball to be ____ kg•m/s.
|
a. -2.5
|
b. -10
|
c. -18
|
d. -45
|
e. none of these
|
|
Answer: C
Don't make this harder than it is; the momentum change of an object can be found if the mass and the velocity change are known. In this equation, m=3 kg and the velocity change is -6 m/s. When finding the velocity change, always subtract the initial velocity from the final velocity (vf - vi).
There is a second means of determining the momentum change of an object (though it does not need to be used in this problem). The momentum change can also be found if the force and the time are known. Multiplying force*time yields the impulse and the impulse equals the momentum change.
|
28. A 5-N force is applied to a 3-kg ball to change its velocity from +9 m/s to +3 m/s. The impulse experienced by the ball is ____ N•s.
|
a. -2.5
|
b. -10
|
c. -18
|
d. -45
|
e. none of these
|
|
Answer: C
Impulse is defined as a force acting upon and object for a given amount of time. Impulse can be computed by multiplying force*time. But in this problem, the time is not known. Never fear - the impulse equals the momentum change. The momentum change in this problem is -18 kg•m/s (see question #27). Thus, the impulse is -18 N•s.
|
29. A 5-N force is applied to a 3-kg ball to change its velocity from +9 m/s to +3 m/s. The impulse is encountered by the ball for a time of ____ seconds.
|
a. 1.8
|
b. 2.5
|
c. 3.6
|
d. 10
|
e. none of these
|
|
Answer: C
Use the impulse momentum change theorem with F=5 N, m=3 kg and Delta v=-6 m/s. Solving for time involves the following steps.
t = m*(delta v)/F = (3 kg)*(-6 m/s) / (5 N)
t = 3.6 s
|
30. When a mass M experiences a velocity change of v in a time of t, it experiences a force of F. Assuming the same velocity change of v, the force experienced by a mass of 2M in a time of (1/2)t is ____.
|
a. 2F
|
b. 4F
|
c. (1/2)*F
|
d. (1/4)*F
|
e. none of these
|
|
Answer: B
The impulse-momentum change theorem states that F*t = m*(Delta vel.). This equation can be rearranged to locate the F by itself on one side of the equation; rearranging yields
F = m*(Delta vel.)/t
The equation shows that force is directly related to the mass, directly related to the change in velocity, and inversely related to the time. So any change in mass will result in the same change in force; and any change in time will result in the inverse effect upon the force. In this case, doubling the mass (from M to 2M) will double the force and halving the time (from t to 1/2-t) will double the force. The combined effect of these two changes will make the new force four times bigger than the old force. This is a case of where equations can be a guide to thinking about how a change in one variable (or two variables) impacts other dependent variables.
|
31. When a mass M experiences a velocity change of v in a time of t, it experiences a force of F. Assuming the same velocity change of v, the force experienced by a mass of 2M in a time of (1/4)t is ____.
|
a. 2F
|
b. 8F
|
c. (1/2)*F
|
d. (1/8)*F
|
e. none of these
|
|
Answer: B
The impulse-momentum change theorem states that F*t = m*(Delta vel.). This equation can be rearranged to locate the F by itself on one side of the equation; rearranging yields
F = m*(Delta vel.)/t
The equation shows that force is directly related to the mass, directly related to the change in velocity, and inversely related to the time. So any change in mass will result in the same change in force; and any change in time will result in the inverse effect upon the force. In this case, doubling the mass (from M to 2M) will double the force and quartering the time (from t to 1/4-t) will quadruple the force. The combined effect of these two changes will make the new force eight times bigger than the old force. This is a case of where equations can be a guide to thinking about how a change in one variable (or two variables) impacts other dependent variables.
|
32. When a mass M experiences a velocity change of v in a time of t, it experiences a force of F. Assuming the same velocity change of v, the force experienced by a mass of (1/2)M in a time of (1/2)t is ____.
|
a. 2F
|
b. 4F
|
c. (1/2)*F
|
d. (1/4)*F
|
e. none of these
|
|
Answer: E
The impulse-momentum change theorem states that F*t = m*(Delta vel.). This equation can be rearranged to locate the F by itself on one side of the equation; rearranging yields
F = m*(Delta vel.)/t
The equation shows that force is directly related to the mass, directly related to the change in velocity, and inversely related to the time. So any change in mass will result in the same change in force; and any change in time will result in the inverse effect upon the force. In this case, halving the mass (from M to 1/2-M) will half the force and halving the time (from t to 1/2-t) will double the force. The combined effect of these two changes will make the new force the same size as the old force. This is a case of where equations can be a guide to thinking about how a change in one variable (or two variables) impacts other dependent variables.
|
33. When a mass M experiences a velocity change of v in a time of t, it experiences a force of F. Assuming the same velocity change of v, the force experienced by a mass of (1/2)M in a time of 4t is ____.
|
a. 2F
|
b. 8F
|
c. (1/2)*F
|
d. (1/8)*F
|
e. none of these
|
|
Answer: D
The impulse-momentum change theorem states that F*t = m*(Delta vel.). This equation can be rearranged to locate the F by itself on one side of the equation; rearranging yields
F = m*(Delta vel.)/t
The equation shows that force is directly related to the mass, directly related to the change in velocity, and inversely related to the time. So any change in mass will result in the same change in force; and any change in time will result in the inverse effect upon the force. In this case, halving the mass (from M to 1/2-M) will halve the force and quadrupling the time (from t to 4t) will quarter the force. The combined effect of these two changes will make the new force eight times smaller (i.e., one-eighth the size) than the old force. This is a case of where equations can be a guide to thinking about how a change in one variable (or two variables) impacts other dependent variables.
|
34. A 0.5-kg ball moving at 5 m/s strikes a wall and rebounds in the opposite direction with a speed of 2 m/s. If the impulse occurs for a time duration of 0.01 s, then the average force (magnitude only) acting upon the ball is ____ Newtons.
|
a. 0.14
|
b. 150
|
c. 350
|
d. 500
|
e. none of these
|
|
Answer: C
This is a relatively simple plug-and-chug into the equation
F*t = m*(Delta vel.)
with m=0.5 kg, t=0.01 s and Delta vel.=-7 m/s. (The change in velocity is -7 m/s since the ball must first slow down from 5 m/s to 0 m/s and then be thrown back in the opposite direction at 2 m/s.) Using these numbers and solving for force yields -350 N. The magnitude of the force is 350 N and the "-" sign indicates the direction of the force.
|
35. If mass and collision time are equal, then impulses are greater on objects which rebound (or bounce).
|
Answer: A
The impulse is equal to the momentum change. And when there is a rebound, the momentum change is larger since there is a larger velocity change. For instance, a ball thrown at a wall at 5 m/s may rebound at -3 m/s yielding a velocity change of -8 m/s. An egg thrown at the same wall at the same speed of 5 m/s hits and stops, thus yielding a velocity change of -5 m/s. More velocity change means more momentum change and thus more impulse.
|
36. Consider the head-on collision between a lady bug and the windshield of a high speed bus. Which of the following statements are true? List all that apply.
- The magnitude of the force encountered by the bug is greater than that of the bus.
- The magnitude of the impulse encountered by the bug is greater than that of the bus.
- The magnitude of the momentum change encountered by the bug is greater than that of the bus.
- The magnitude of the velocity change encountered by the bug is greater than that of the bus.
- The magnitude of the acceleration encountered by the bug is greater than that of the bus.
|
Answer: D and E
In any collision between two objects, the force, impulse, and momentum change are the same for each object. (This makes statements A, B, and C false.) However, the smaller mass object encounters a greater acceleration and velocity change. (This makes statements D and E true).
|
Part C: Diagramming and Analysis
For Questions #37-#40: Consider the before- and after-collision momentum vectors in the diagram below. Determine the magnitude and direction of the system momentum before and after the collision and identify whether or not momentum is conserved. Finally, determine the magnitude and direction of the net external impulse encountered by the system during the collision.
|
37.
|
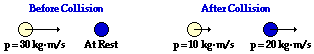
|
|
System Momentum Before Collision:
|
30 kg•m/s, right
|
|
System Momentum After Collision:
|
30 kg•m/s, right
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N
|
|
Answer: See table above.
Before the collision, the two momentum values can be added: 30 units + 0 = 30 units. (An object at rest has zero momentum.) After the collision, the momentum vectors can be added: 30 units + 0 = 30 units. In each case, the total momentum is in the direction of the arrows. Since the total system momentum before the collision is the same as it is after the collision, the total momentum of the system can be considered to be conserved. As such, there is no net external impulse upon the system. It is considered isolated.
|
|
38.
|
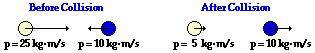
|
|
System Momentum Before Collision:
|
15 kg•m/s, right
|
|
System Momentum After Collision:
|
15 kg•m/s, right
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N•s |
|
Answer: See table above.
The dark ball has a leftward momentum, so its momentum must be assigned a - sign to distinguish its momentum from the rightward momentum of the light-colored ball. So before the collision, the system has +25 units + -10 units of momentum - a total of +15 units. After the collision, the total momentum of the system is + 15 units (the "+" is the designated sign for a rightward momentum). Since the system momentum is the same before as after the collision, momentum is conserved and the system is considered isolated from net external impulses.
|
|
39.
|
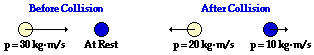
|
|
System Momentum Before Collision:
|
30 kg•m/s, right
|
|
System Momentum After Collision:
|
10 kg•m/s, left
|
|
Is momentum conserved?
|
No
|
|
Net External Impulse During Collision:
|
40 N•s, left
|
|
Answer: See table above.
Since the light-colored ball has a leftward momentum, the leftward direction will be designated as the negative direction. Thus, the before- and after-collision calculations are:
Before: +30 units + 0 units = +30 units
After: -20 units + 10 units = -10 units
The total momentum of the system has changed by -40 units. Thus, momentum is not conserved and the system experiences a net external impulse of -40 units or 40•N s, leftward.
|
|
40.
|
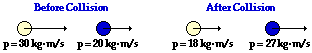
|
|
System Momentum Before Collision:
|
50 kg•m/s, right
|
|
System Momentum After Collision:
|
45 kg•m/s, right |
|
Is momentum conserved?
|
No |
|
Net External Impulse During Collision:
|
5 N•s, left
|
|
Answer: See table above.
The summations of system momentum before and after the collision are:
Before: +30 units + +20 units = +50 units.
After: +18 units + +27 units = +45 units.
The system loses 5 units of momentum. Thus, momentum is not conserved. There must be a net external impulse of -5 units upon the system. That impulse is 5 N•s, left. (The left is equivalent to saying negative.)
|
For Questions #41-#44: Repeat the procedure performed in Questions #37-#40. Note that these diagrams give velocity and mass values before and after the collision.
|
41.
|
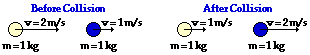
|
|
System Momentum Before Collision:
|
3 kg•m/s, right
|
|
System Momentum After Collision:
|
3 kg•m/s, right
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N•s
|
|
Answer: See table above.
Before Collision: 1 kg) * (+2 m/s) + (1 kg) * (1 m/s ) = 3 kg m/s
After Collision: (1 kg) * (1 m/s) + (1 kg) * (2 m/s ) = 3 kg m/s
The total system momentum is the same before and after the collision. Thus, momentum is conserved and there is no net external impulse on the system.
|
|
42.
|
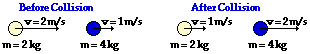
|
|
System Momentum Before Collision:
|
8 kg•m/s, right
|
|
System Momentum After Collision:
|
10 kg•m/s, right
|
|
Is momentum conserved?
|
No
|
|
Net External Impulse During Collision:
|
2 N•s, right
|
|
Answer: See table above.
Before Collision: (2 kg) * (2 m/s) + (4 kg) * (1 m/s ) = 8 kg m/s
After Collision: (1 kg) * (2 m/s) + (4 kg) * (2 m/s ) = 10 kg m/s
The total system momentum is NOT the same before and after the collision. Thus, momentum is NOT conserved. There is a net external impulse on the system which is equal to the momentum change of the system. The net external impulse is +2 kg•m/s.
|
|
43.
|
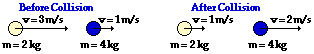
|
|
System Momentum Before Collision:
|
10 kg•m/s, right
|
|
System Momentum After Collision:
|
10 kg•m/s, right
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N•s
|
|
Answer: See table above.
Before Collision: (2 kg) * (3 m/s) + (4 kg) * (1 m/s ) = 10 kg m/s
After Collision: (2 kg) * (1 m/s) + (4 kg) * (2 m/s ) = 10 kg m/s
The total system momentum is the same before and after the collision. Thus, momentum is conserved and there is no net external impulse on the system.
|
|
44.
|
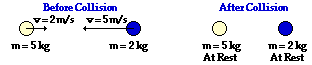
|
|
System Momentum Before Collision:
|
0 kg•m/s
|
|
System Momentum After Collision:
|
0 kg•m/s
|
|
Is momentum conserved?
|
Yes
|
|
Net External Impulse During Collision:
|
0 N•s
|
|
Answer: See table above.
Before Collision: (5 kg) * (2 m/s) + (2 kg) * (-5 m/s ) = 0 kg m/s
After Collision: (5 kg) * (0 m/s) + (2 kg) * (0 m/s ) = 0 kg m/s
The total system momentum is the same before and after the collision. Thus, momentum is conserved and there is no net external impulse on the system.
|
For Questions #45-#49, determine the unknown velocity value. Assume that the collisions occur in an isolated system.
|
General Note about Questions #45-#49:
In each of these problems, an expression for the total momentum before the collision is written by summing the product of mass and velocity for each object. The same is done with the total momentum after the collision. One must be careful to assign a negative momentum to any object which is moving leftward. When the velocity of an object is not known, the variable v should be placed in the expression in place of the actual velocity value. The two expressions for total momentum before and after the collision are set equal to each other and algebraic operations are used to determine the unknown velocities. This method is shown below.
|
|
45.
|
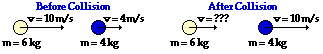
|
|
Answer: 6 m/s
Before Collision: (6 kg) * (10 m/s) + (4 kg) * (4 m/s ) = 76 kg m/s
After Collision: (6 kg) * v + (4 kg) * (10 m/s ) = (6 kg) * v + 40 kg m/s
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
76 = 6v + 40
36 = 6v
v = 6 m/s
|
|
46.
|
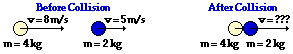
|
|
Answer: 7 m/s
Before Collision: (4 kg) * (8 m/s) + (2 kg) * (5 m/s ) =
After Collision: (4 kg) * v + (2 kg) * v
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
42 = 6 * v
v = 7 m/s
|
|
47.
|
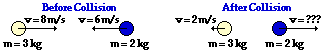
|
|
Answer: 9 m/s
Before Collision: (3 kg) * (8 m/s) + (2 kg) * (-6 m/s ) = 12 kg m/s
After Collision: (3 kg) * (-2 m/s) + (2 kg) * v = -6 kg m/s + (2 kg) * v
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
12 = -6 + 2v
18 = 2v
v = 9 m/s
|
|
48.
|
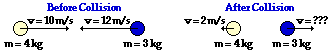
|
|
Answer: 4 m/s
Before Collision: (4 kg) * (10 m/s) + (3 kg) * (-12 m/s ) = 4 kg m/s
After Collision: (4 kg) * (-2 m/s) + (3 kg) * v = -8 kg m/s+ (3 kg) * v
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
4 = -8 + 3v
12 = 3v
v = 4 m/s
|
|
49.
|
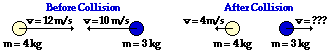
|
|
Answer: 11.3 m/s
Before Collision: (4 kg) * (12 m/s) + (3 kg) * (-10 m/s ) = 18 kg m/s
After Collision: (4 kg) * (-4 m/s) + (3 kg) * v = -16 kg m/s + (3 kg) * v
(In the following steps, the units are dropped so that the algebra can be more easily followed.)
18 = -16 + 3v
34.0 = 3v
v = 11.3 m/s
|
For Questions #50-#52, determine the total kinetic energy of the system before and after the collision and identify the collision as being either perfectly elastic, partially inelastic/elastic or perfectly inelastic.
|
50.
|
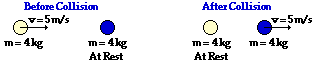
|
|
Total System Kinetic Energy Before Collision:
|
50 J
|
|
Total System Kinetic Energy After Collision:
|
50 J
|
|
Perfectly Elastic, Partially Inelastic/Elastic or Perfectly Inelastic?
|
Perfectly Elastic
|
|
Answer: See table above.
Before Collision: KEtotal = 0.5•(4 kg)•(5 m/s)2 + 0.5•(4 kg)•(0 m/s)2 = 50 J
After Collision: KEtotal = 0.5•(4 kg)•(0 m/s)2 + 0.5•(4 kg)•(5 m/s)2 = 50 J
The system kinetic energy is conserved in this collision. That is, the total kinetic energy is the same before the collision as after the collision. The critical requirement for a collision to be perfectly elastic is that the total system kinetic energy is conserved. Thus, this collision is a perfectly elastic collision.
|
|
51.
|
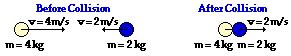
|
|
Total System Kinetic Energy Before Collision:
|
36 J
|
|
Total System Kinetic Energy After Collision:
|
12 J
|
|
Perfectly Elastic, Partially Inelastic/Elastic or Perfectly Inelastic?
|
Perfectly Inelastic
|
|
Answer: See table above.
Before Collision: KEtotal = 0.5•(4 kg)•(4 m/s)2 + 0.5•(2 kg)•(-2 m/s)2 = 36 J
After Collision: KEtotal = 0.5•(4 kg)•(2 m/s)2 + 0.5•(2 kg)•(2 m/s)2 = 12 J
The system kinetic energy is NOT conserved in this collision. That is, the total kinetic energy is NOT the same before the collision as after the collision. The critical requirement for a collision to be perfectly inelastic is that the colliding objects move as a single unit with the same velocity after the collision. These objects do "stick together" after the collision and move as a single unit at the same velocity. Thus, the collision is a perfectly inelastic collision.
[ #1 | #2 | #3 | #4 | #5 | #6 | #7 | #8 | #9 | #10 | #11 | #12 | #13 | #14 | #15 | #16 | #17 | #18 | #19 | #20 | #21 | #22 | #23 | #24 | #25 | #26 | #27 | #28 | #29 | #30 | #31 | #32 | #33 | #34 | #35 | #36 | #37 | #38 | #39 | #40 | #41 | #42 | #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 | #51 | #52 | #53 | #54 | #55 | #56 | #57 | #58 | #59 | #60 | #61 | #62 | #63 | #64 | #65 | #66 | #67 | #68 | #69 | #70 | #71 | #72 ]
|
|
52.
|
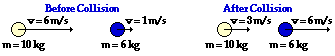
|
|
Total System Kinetic Energy Before Collision:
|
183 J
|
|
Total System Kinetic Energy After Collision:
|
153 J |
|
Perfectly Elastic, Partially Inelastic/Elastic or Perfectly Inelastic?
|
Partially Inelastic/Elastic
|
|
Answer: See table above.
Before Collision: KEtotal = 0.5•(10 kg)•(6 m/s)2 + 0.5•(6 kg)•(1 m/s)2 = 183 J
After Collision: KEtotal = 0.5•(10 kg)•(3 m/s)2 + 0.5•(6 kg)•(6 m/s)2 = 153 J
The system kinetic energy is NOT conserved in this collision. That is, the total kinetic energy is NOT the same before the collision as after the collision. Thus, the collision does not meet the criterion for a perfectly elastic collision. The objets do NOT "stick together" after the collision; they move with different speeds. Thus, the collision does not meet the criterion for a perfectly inelastic collision. This collision is a partially inelastic/elastic collision.
|
Part D: Qualitative Relationships Between Variables
53. An object with a mass M and a velocity v has a momentum of 32 kg•m/s. An object with a mass of ...
- .. 2M and a velocity of 2v would have a momentum of 64 kg•m/s.
- ... 2M and a velocity of 0.5v would have a momentum of 32 kg•m/s.
- ... 0.5M and a velocity of 2v would have a momentum of 32 kg•m/s.
- ... 0.5M and a velocity of 0.5v would have a momentum of 8 kg•m/s.
- ... 4M and a velocity of v would have a momentum of 128 kg•m/s.
- ... 4M and a velocity of 0.5v would have a momentum of 64 kg•m/s.
- ... 0.5M and a velocity of 4v would have a momentum of 64 kg•m/s.
- ... 3M and a velocity of 2v would have a momentum of 192 kg•m/s.
|
Answer: See Answers above.
Momentum is the product of mass and velocity. As such, the momentum of an object is directly proportional to the mass and directly proportional to the velocity. If the mass of an object is altered by some factor, then the momentum of the object is altered by that same factor. So if the mass is doubled, the momentum is doubled; the new value would be two times the original value. And if the mass is tripled, then the momentum is tripled; the new value would be three times the original value. If the velocity of an object is altered by some factor, then the momentum of the object is altered by that same factor. So if the velocity is doubled, the momentum is doubled; the new value would be two times the original value. And if the velocity is tripled, then the momentum is tripled; the new value would be three times the original value. This is shown in the work below.
a. New value = 32 kg m/s • 2 • 2 = 128 kg•m/s
b. New value = 32 kg m/s • 2 • 0.5 = 32 kg•m/s
c. New value = 32 kg m/s • 0.5 • 2 = 32 kg•m/s
d. New value = 32 kg m/s • 0.5 • 0.5 = 8 kg•m/s
e. New value = 32 kg m/s • 4 • 1 = 128 kg•m/s
f. New value = 32 kg m/s • 4 • 0.5 = 64 kg•m/s
g. New value = 32 kg m/s • 0.5 • 4 = 64 kg•m/s
h. New value = 32 kg m/s • 3 • 2 = 192 kg•m/s
|
54. An object with a mass M and a velocity v undergoes a collision and encounters a force of F for a time of t. The collision brings the object to a final rest position ...
- ... If the object had a mass of 2M and a velocity of v, then it would need an impulse which is 2 F•t in order to be brought to rest.
- ... If the same object encountered a force of 2F, then it would bring it to rest in a time of 0.5 t, The impulse would be the same size and the momentum change would be the same size.
- ... If the same object encountered a force of 10F, then it would bring it to rest in a time of 0.1 t, The impulse would be the same size and the momentum change would be the same size.
- ... If the same object encountered a force of 0.2F, then it would bring it to rest in a time of 5 t, The impulse would be the same (size and the momentum change would be the same size.
- ... If the object had a mass of 2M and a velocity of v encountered a force of 4F, then it would be brought to rest in a time of 0.5 t. The impulse would be 2 times the original impulse and the momentum change would be 2 times the original impulse.
- ... If the object had a mass of 2M and a velocity of 2v encountered a force of 4F, then it would be brought to rest in a time of 1.0 t. The impulse would be 4 times the original impulse and the momentum change would be 4 times the original impulse.
- ... If the object had a mass of 0.5M and a velocity of 4v encountered a force of 2F, then it would be brought to rest in a time of 1.0 t. The impulse would be 2 times the original impulse and the momentum change would be 2 times the original impulse.
|
Answer: See Answers above.
In a collision, the impulse encountered by an object causes and is equal to the momentum change of the object. For objects being brought to rest, the change in momentum is simply equal to the original momentum. An object with twice the momentum would require twice the impulse to stop it. An object with one-half the momentum would require one-half the impulse to stop it. The momentum is the product of mass and velocity, so any alteration in the mass or the velocity or both would alter the required impulse by that same factor. The impulse results from a force acting over time and is the product of force and time. So twice the impulse can be achieved by the same force acting for twice the time or twice the force acting for the same time or even one-half the force acting for four times the time. These principles are illustrated below.
a. Two times the mass means two times the original momentum. Two times the impulse would be required to stop an object with two times the momentum.
b. If the same object with the same momentum (M•v) were stopped by twice the original force, then only one-half the original time would be required to stop it. Since the momentum change has not been altered in this case (an object with a momentum of M•v is still being stopped), the impulse is not altered either.
c. If the same object with the same momentum (M•v) were stopped by ten times the original force, then only one-tenth the original time would be required to stop it. Since the momentum change has not been altered in this case (an object with a momentum of M•v is still being stopped), the impulse is not altered either.
d. If the same object with the same momentum (M•) were stopped by one-fifth the original force, then five times the original time would be required to stop it. Since the momentum change has not been altered in this case (an object with a momentum of M•v is still being stopped), the impulse is not altered either.
e. If an object with twice the mass is being stopped, then twice the momentum change would occur. Two times the momentum change means that an impulse which is two times the original impulse would be required. To achieve two times the impulse, the product of force and time must be doubled. Since the force is four times bigger, the time needs to be one-half the original time.
f. If an object with twice the mass and twice the velocity is being stopped, then four times the momentum change would occur. Four times the momentum change means that an impulse which is four times the original impulse would be required. To achieve four times the impulse, the product of force and time must be quadrupled. Since the force is four times bigger, the time needs to be the same as the original time.
g. If an object with one-half the mass and four times the velocity is being stopped, then twice the momentum change would occur. Two times the momentum change means that an impulse which is two times the original impulse would be required. To achieve two times the impulse, the product of force and time must be doubled. Since the force is two times bigger, the time needs to be the same as the original time.
|
55. Two carts are placed next to each other on a low-friction track. The carts are equipped with a spring-loaded mechanism which allows them to impart an impulse to each other. Cart A has a mass of M and Cart B has a mass of M. The spring-loaded mechanism is engaged and then released. The impulse causes Cart A to be propelled forward with a velocity of 40 cm/s.
- Cart B will be propelled backward with a velocity of 40 cm/s.
- ... If Cart B had a mass of 2M then it would be propelled backwards with a velocity of 20 cm/s.
- ... If Cart B had a mass of 0.5M then it would be propelled backwards with a velocity of 80 cm/s.
- ... If Cart B has a mass of 2M then it would be propelled backwards with a momentum which is the same as the original momentum.
- ... If Cart B has a mass of 2M then it would encounter an impulse which is the same as the original impulse.
|
Answer: See Answers above.
Cart A and Cart B begin at rest. The original momentum of the system is 0 units. If momentum is to be conserved, the total momentum of the system of two carts must also be 0 units. This means that the momentum of Cart A must have the same magnitude as the momentum of Cart B. That is, after the spring is released, the product of mass and velocity for Cart A must equal the product of mass and velocity for Cart B. This principle is illustrated in the reasoning below.
a. Since the two carts have the same mass, they must also have the same velocity in order to have the same magnitude of momentum. The post-explosion velocity of Cart B is 40 cm/s.
b. If Cart B has twice the mass as Cart A, then it must be propelled backwards with one-half the velocity. The post-explosion velocity of Cart B is 20 cm/s.
c. If Cart B has one-half the mass As Cart A, then it must be propelled backwards with two times the velocity. The post-explosion velocity of Cart B is 80 cm/s.
d. Changing the mass of either one of the carts does not alter the impulse or the momentum change which it experiences. An alteration in the mass merely alters the velocity with which the cart is propelled. A twice-as-massive cart acquires one-half the original velocity but the momentum change is the same as the original momentum change.
e. Changing the mass of either one of the carts does not alter the impulse or the momentum change which it experiences. An alteration in the mass merely alters the velocity with which the cart is propelled. A twice-as-massive cart acquires one-half the original velocity but the impulse is the same as the original impulse.
|
56. A cart with a mass of M is moving along a low-friction track with a speed of 60 cm/s. A brick is gently dropped from rest upon the cart. After the collision the cart and brick move together.
- ... If the brick has a mass of 2M, then the post-collision speed of the two objects will be 20 cm/s.
- ... If the brick has a mass of 3M, then the post-collision speed of the two objects will be 15 cm/s.
- ... If the brick has a mass of 4M, then the post-collision speed of the two objects will be 12 cm/s.
- ... If the brick has a mass of 5M, then the post-collision speed of the two objects will be 10 cm/s.
- ... If the brick has a mass of 0.5M, then the post-collision speed of the two objects will be 40 cm/s.
- ... If the brick has a mass of 0.25M, then the post-collision speed of the two objects will be 48 cm/s.
|
Answer: See Answers above.
This is a special case of a perfectly inelastic collision. The total system momentum before the collision is possessed solely by the moving cart. After the collision, the total system momentum is the combined momentum of the brick and the cart. Since the brick and cart travel at the same velocity after the collision, the momentum is simply the sum of their masses multiplied by their velocity. In effect, the total mass which is in motion is increased by some factor as a result of the subsequent motion of the brick. For momentum to be conserved, the velocity of the cart (and the brick which is on top of it) must be decreased by that same factor. This principle is used to reason towards the answers to these questions.
a. Adding a brick with a mass of 2M will increase the total mass in motion from M (the cart's mass) to 3M. This threefold increase in mass is accompanied by a threefold decrease in velocity. The new velocity is one-third the original value. The cart and brick move forward with a velocity of 20 cm/s.
b. Adding a brick with a mass of 3M will increase the total mass in motion from M (the cart's mass) to 4M. This fourfold increase in mass is accompanied by a fourfold decrease in velocity. The new velocity is one-fourth the original value. The cart and brick move forward with a velocity of 15 cm/s.
c. Adding a brick with a mass of 4M will increase the total mass in motion from M (the cart's mass) to 5M. This fivefold increase in mass is accompanied by a fivefold decrease in velocity. The new velocity is one-fifth the original value. The cart and brick move forward with a velocity of 12 cm/s.
d. Adding a brick with a mass of 5M will increase the total mass in motion from M (the cart's mass) to 6M. This six-fold increase in mass is accompanied by a six-fold decrease in velocity. The new velocity is one-sixth the original value. The cart and brick move forward with a velocity of 10 cm/s.
e. Adding a brick with a mass of 0.5M will increase the total mass in motion from M (the cart's mass) to 1.5M. This increases the mass by a factor of 1.5 and is accompanied by a decrease in velocity by a factor of 1.5. The new velocity is two-thirds the original value. The cart and brick move forward with a velocity of 40 cm/s.
f. Adding a brick with a mass of 0.25M will increase the total mass in motion from M (the cart's mass) to 1.25M. This increases the mass by a factor of 1.25 and is accompanied by a decrease in velocity by a factor of 1.25. The new velocity is four-fifths the original value. The cart and brick move forward with a velocity of 48 cm/s.
|
Part E: Problem-Solving
57. A 0.530-kg basketball hits a wall head-on with a forward speed of 18.0 m/s. It rebounds with a speed of 13.5 m/s. The contact time is 0.100 seconds. (a) determine the impulse with the wall, (b) determine the force of the wall on the ball.
|
Answer: Answer: (a) -16.7 N s; (b) -167 N
Given: m = 0.530 kg; vi = 18.0 m/s; vf = 13.5 m/s; t = 0.100 s
Find: (a) Impulse, (b) Force
(a) Impulse = Momentum Change = m•Delta v = m•(vf - vi)= (0.530 kg)•( -13.5 m/s - 18.0 m/s)
Impulse = -16.7 kg•m/s = -16.7 N•s
where the "-" indicates that the impulse was opposite the original direction of motion.
(Note that a kg•m/s is equivalent to a N•s)
(b) The impulse is the product of force and time. So if impulse is known and time is known, force can be easily determined.
Impulse = F•t
F = Impulse/t = (-16.7 N s) / (0.100 s) = -167 N
where the "-" indicates that the impulse was opposite the original direction of motion.
|
58. A 4.0-kg object has a forward momentum of 20. kg•m/s. A 60. N•s impulse acts upon it in the direction of motion for 5.0 seconds. A resistive force of 6.0 N then impedes its motion for 8.0 seconds. Determine the final velocity of the object.
|
Answer: vf = 8.0 m/s
This question is best thought about conceptually using the principle that an objects momentum is changed when it encounters an impulse and the amount of change in momentum is equal to the impulse which it encounters.
Here an object starts with 20 units (kg•m/s) of momentum. It then encounters an impulse of 60 units (N•s) in the direction of motion. A 60-unit impulse will change the momentum by 60 units, either increasing or decreasing it. If the impulse is in the direction of an object's motion, then it will increase the momentum. So now the object has 80 units (kg•m/s) of momentum. The object then encounters a resistive force of 6.0 N for 8.0 s. This is equivalent to an impulse of 48 units (N•s). Since this impulse is "resistive" in nature, it will decrease the object's momentum by 48 units. The object now has 32 units of momentum. The question asks for the object's velocity after encountering these two impulses. Since momentum is the product of mass and velocity, the velocity can be easily determined.
p = m•v
vfinal = pfinal / m = (32 kg m/s) / (4.0 kg) = 8.0 m/s
|
59. A 3.0-kg object is moving forward with a speed of 6.0 m/s. The object then encounters a force of 2.5 N for 8.0 seconds in the direction of its motion. The object then collides head-on with a wall and heads in the opposite direction with a speed of 5.0 m/s. Determine the impulse delivered by the wall to the object.
|
Answer: 53 N•s
Like the previous problem, this problem is best solved by thinking through it conceptually using the impulse-momentum change principle.
Here the object begins with a momentum of 18 units (kg•m/s). The object encounters a force of 2.5 N for 8.0 seconds. This is equivalent to an impulse of 20 units (N•s). Since this impulse acts in the direction of motion, it changes the object's momentum from 18 units to 38 units. A final impulse is encountered when colliding with a wall. Upon rebounding, the object has a momentum of -15 units (kg•m/s). The -15 is the product of mass (3 kg) and velocity (-5 m/s). The "-" sign is used since the object is now moving in the opposite direction as the original motion. The collision with the wall changed the object's momentum from +38 units to -15 units. Thus, the collision must have resulted in a 53-unit impulse since it altered the object's momentum by 53 units.
|
60. A 46-gram tennis ball is launched from a 1.35-kg homemade cannon. If the cannon recoils with a speed of 2.1 m/s, determine the muzzle speed of the tennis ball.
|
Answer: 62 m/s
Given: mball = 46 g = 0.046 kg; mcannon = 1.35 kg; vcannon = -2.1 m/s
Find: vball = ???
The ball is in the cannon and both objects are initially at rest. The total system momentum is initially 0. After the explosion, the total system momentum must also be 0. Thus, the cannon's backward momentum must be equal to the ball's forward momentum.
mcannon • vcannon = -mball • vball
(1.35 kg) • (-2.1 m/s) = (0.046 kg) • vball
vball = (1.35 kg) • (2.1 m/s) / (0.046 kg) = 61.63 m/s = ~62 m/s
|
You Might Also Like ...
Users of The Review Session are often looking for learning resources that provide them with practice and review opportunities that include built-in feedback and instruction. If that is what you're looking for, then you might also like the following:
- The Calculator Pad
The Calculator Pad includes physics word problems organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to approach and solve the problem. It's a perfect resource for those wishing to improve their problem-solving skills.
Visit: The Calculator Pad Home | Calculator Pad - Momentum and Collisions
- Minds On Physics the App Series
Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the series covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-like environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resource for those wishing to refine their conceptual reasoning abilities. Part 3 of the series includes topics in Momentum and Collisions.
Visit: MOP the App Home || MOP the App - Part 3