Lesson 1: Solubility of Salts

Part c: Solubility and Common Ion Effects

Part a: The Solubility Product Constant, K_sp
Part b: Solubility and K_sp
Part c: Solubility and Common Ion Effects

 

The Big Idea

The page explains how solubility isn’t fixed. When an insoluble salt is dissolved in a solution that already contains one of its ions, the equilibrium system responds by reducing the solubility. Learn the concept and the mathematics in the usual organized presentation.

 

What is a Common Ion?

The solubility of slightly or sparingly soluble salts (sometimes referred to as insoluble salts) in pure water was discussed in Lesson 1b. The ion concentration was determined by assuming that the dissociating salt was the only source of the ions. This is the case for salts dissolving in pure water. An ICE table analysis indicates that the initial concentration of the ions was 0 M.

 
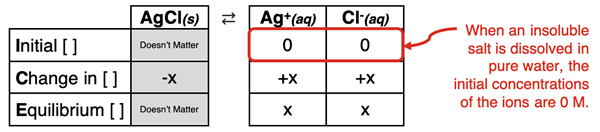
In this part of Lesson 1, we will discuss situations in which the insoluble salt is dissolved in a solution containing a common ion. This most often happens when the solution contains a soluble salt having an ion in common with the insoluble salt. For instance, if AgCl (an insoluble salt) is dissolved in a solution of 0.10 M NaCl (a soluble salt), the chloride ion is a common ion. It is present in both salts or common to both salts. As such, the chloride ion is already in the solution before the insoluble salt dissociates. Its presence will affect the solubility of the AgCl.

 
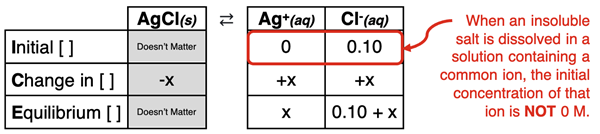
The beaker diagrams below represent situations in which an insoluble salt is being dissolved in a solution containing a common ion. A soluble salt that has an ion in common with the insoluble salt is present in the solution before the insoluble salt is added. Each of these situations leads to what we refer to as the common ion effect.

 
 
 

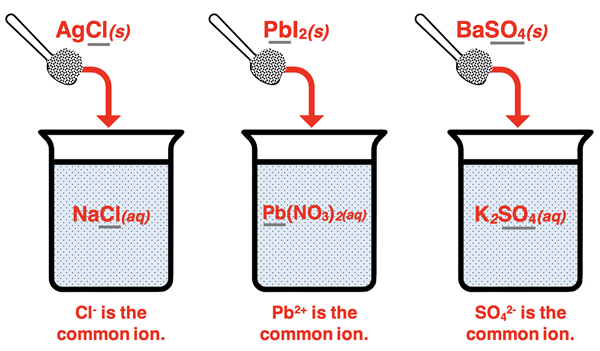
What is the Common Ion Effect?

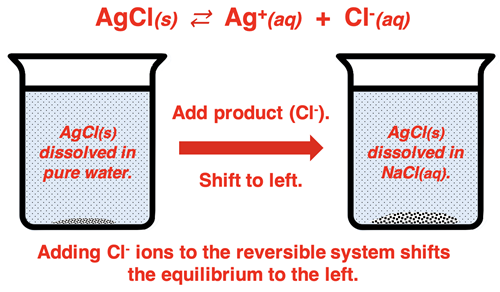
When an insoluble salt is dissolved in a solution containing a common ion, the solubility of the salt decreases. While the K_sp of the salt is unaffected by the common ion, the amount of salt that can dissociate before equilibrium is reached is significantly reduced. This decrease in solubility due to the presence of a common ion can be explained by LeChatelier’s principle. If you imagine the two ions in otherwise pure water in equilibrium with undissolved solid, the addition of one of the product ions disrupts the equilibrium and shift the reaction towards the left. This LeChatelier shift towards reactants reduces the amount of solid that is dissolving.

 
The following statements illustrate the common ion effect. Observe the significant decrease in solubility that occurs when the insoluble salt is dissolved in a solution of a soluble salt that contains a common ion.

• The solubility of AgCl in pure water is 1.3x10^-5 mol/L. But its solubility in a 0.10 M NaCl solution is 1.8x10^-9 mol/L.
• The solubility of CaF₂ in pure water is 2.1x10^-4 mol/L. But its solubility in a 0.10 M NaF solution is 3.5x10^-9 mol/L.
• The solubility of AlPO₄ in pure water is 9.9x10^-11 mol/L. But its solubility in a 0.10 M K₃PO₄ solution is 9.8x10^-20 mol/L.

 
 

A Simplifying Assumption

The mathematical analysis of the common ion effect can be algebraically complex. Fortunately, there is an assumption that is commonly made that simplifies the algebra. The assumption is that the concentration of the common ion in the solution is primarily due to the contribution made by the soluble salt. If the soluble salt dissociates to produce the common ion with a concentration of 0.10 M, then the dissolving of the insoluble salt contributes such a small amount to this concentration value that it will still be approximately 0.10 M. For instance, if x mole/L of the common ion is produced by the insoluble salt’s dissociation, then the equilibrium concentration would be 0.10 + x. For insoluble salts with very small K_sp values, x is generally so small that ...
     
 
 

Case Comparison - Solubility of AgCl With and Without a Common Ion

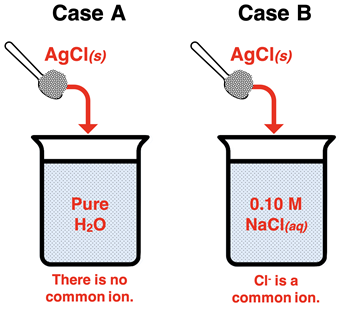
Let’s conduct a mathematical analysis comparing the solubility of AgCl in pure water (Case A) to the solubility in a 0.10 M solution of NaCl (Case B). In both cases, the AgCl is an ever-so-slightly soluble salt with a K_sp value of 1.8 × 10^-10. It dissociates to produce the Ag⁺ and Cl^- ions:
   
When dissolved in pure water, there is no common ion effect. When dissolved in the 0.10 M NaCl(aq) solution, there is a common ion effect. The chloride ion is the common ion. Since NaCl is a soluble salt, the concentration of Cl^- is initially 0.10 M. We will account for this initial concentration in an ICE table.  For both Case A and Case B, we can write the solubility product constant equation as:
   

The ICE tables and subsequent analysis for the two cases are shown below.

   
The mathematics shows that the presence of the common ion (Cl^-) in Case B causes a noticeably lower solubility for the insoluble salt. This is the common ion effect!
   
 
 

Step-by-Step Procedure for Solving a Common Ion Problem

The above analysis depicts a procedural approach to the solution of a common ion problem for an insoluble salt dissolved in a solution of a soluble salt. The procedure can be described by the following steps.

1. Write the balanced chemical equation for the dissociation of the insoluble salt. (Need help? Learn More.)
2. Write the K_sp equation for the reaction.  (Need help? Learn More.)
3. Identify the common ion present in the soluble salt and use the concentration of the soluble salt to determine the concentration of the common ion in the solution.
4. Set up an ICE table. Use the initial concentration of the common ion in the top row of the table. Use the variable x to represent the amount of solid that dissolves. Use the simplifying assumption to reduce the math complexity.
5. Substitute the K_sp value and the expressions for the equilibrium concentrations of the ions into the K_sp equation from Step 2.
6. Use algebra to solve for the x; the value of x is the solubility of the insoluble salt.

 
 
 

Example 1 - Dissolving CaF₂ in a 0.10 M NaF Solution

Calcium fluoride is an insoluble salt with a K_sp value of 3.5 × 10^-11. Determine its solubility in a 0.10 M solution of NaF.
 

Solution

Step 1: The equation for the dissociation of CaF₂ is:  
Step 2:  The K_sp equation is:  
Step 3:  The CaF₂ is being dissolved in a solution of NaF. This solution contains F^- ions; it is the common ion. The concentration of the F- in this solution is initially 0.10 M.
 
Step 4:  The completed ICE table is shown below. Before dissociation, there is no Ca²⁺ ion in the solution but the F^- ion is present with a concentration of 0.10 M; that’s the Initial row. An unknown amount of ions are produced (“x” and “2x”); the coefficients in the balanced equation are used for this Change row. The Equilibrium row of an ICE table is always determined by adding the Change row to the Initial row. We wish to determine x. Since solids are not included in the equilibrium constant expression, we do not worry about their concentrations; that explains why the first column is greyed out.
   
Step 5:  The K_sp value and the last row of the ICE table are substituted into the equation written in Step 2. Note how the simplifying assumption has been used for the chloride ion concentration: 0.10 + 2x ≈ 0.10.
   
Step 6:  Algebra is used to solve for x. The value of x is the solubility. Perform the algebra as slowly as your comfort level requires; do not rush! Slowing down is often the fastest way to a successful finish.
   
 
 

Example 2 - Dissolving BaSO₄ in a 0.10 M Na₂SO₄ Solution

Barium sulfate is an insoluble salt with a K_sp value of 1.1 × 10^-10. Determine its solubility in a 0.10 M solution of Na₂SO₄.
 

Solution

Step 1: The equation for the dissociation of BaSO₄ is:  
Step 2:  The K_sp equation is:  
Step 3:  The BaSO₄ is being dissolved in a solution of Na₂SO₄. This solution contains SO₄^2- ions; it is the common ion. The concentration of the SO₄^2- in this solution is initially 0.10 M.
 
Step 4:  The completed ICE table is shown below. Before dissociation, there is no Ba²⁺ ion in the solution but the SO₄^2- ion is present with a concentration of 0.10 M; that’s the Initial row. An unknown amount of ions are produced (“x”); the coefficients in the balanced equation are used for this Change row. The Equilibrium row of an ICE table is always determined by adding the Change row to the Initial row. We wish to determine x. Since solids are not included in the equilibrium constant expression, we do not worry about their concentrations; that explains why the first column is greyed out.
   
Step 5:  The K_sp value and the last row of the ICE table are substituted into the equation written in Step 2. Note how the simplifying assumption has been used for the chloride ion concentration: 0.10 + x ≈ 0.10.
   
Step 6:  Algebra is used to solve for x. The value of x is the solubility.
   
 
 
 

Before You Leave - Practice and Reinforcement

Now that you've done the reading, take some time to strengthen your understanding and to put the ideas into practice. Here's some suggestions.
 

• The Check Your Understanding section below includes questions with answers and explanations. It provides a great chance to self-assess your understanding.
• Download our Study Card on Common Ion Effects for Insoluble Salts. Save it to a safe location and use it as a review tool. (Coming Soon.)

 
 
 

Check Your Understanding of the Common Ion Effect

Use the following questions to assess your understanding of the common ion effect and your skill at solving common ion problems. Tap the Check Answer buttons when ready.
 
1. Identify the following statements as being TRUE or FALSE:

1. The common ion is always an anion. 
   
   Check Answer
   Answer: False
   
   The common ion can be either a cation or an anion. It simply depends on what ion the soluble salt and the insoluble salt have in common.
   
    
   
    
    
2. The presence of a common ion will decrease the K_sp of the insoluble salt. 
   
   Check Answer
   Answer: False
   
   The solubility is changed by the common ion; but the K_sp remains the same with or without a common ion.
   
    
   
    
    
3. The presence of a common ion can either increase or decrease the solubility, depending on whether it is positively or negatively charged. 
   
   Check Answer
   Answer: False
   
   The presence of the common ion always decreases the solubility.
   
    
   
    
    
4. The effect that a common ion has upon solubility is not explainable. We know it changes the solubility but we don’t fully understand why. 
   
   Check Answer
   Answer: False
   
   The effect is highly explainable, both conceptually by the LeChatelier's principle and mathematically using an ICE table analysis.
   
    
   
    
    
5. Common ion problems are not possible to solve without making a simplifying assumption. 
   
   Check Answer
   Answer: False
   
   They can be solved with or without the simplifying assumption. The solution without making the assumption becomes very algebraically complicated and often results in a value of x that is so small that it has no significant effect upon the answer. Thus, we make the assumption and solve the problem more quickly with very little sacrifice of accuracy.
   
    
   
    
    
6. Common ion problems are best solved by assuming that the concentration of the common ion is the average of what is contributed by the soluble salt and the insoluble salt. 
   
   Check Answer
   Answer: False
   
   This is actually the best way (or at least one way) to miss the problem. Don't do that!
   
    
   
    
    

 
 
2. For the following situations, identify the symbol of the common ion and its initial molar concentration.
a. CaCO₃ dissolving in a solution of 0.10 M CaCl₂.

b. CaCO₃ dissolving in a solution of 0.10 M Na₂CO₃.



c. CuCl dissolving in a solution of 0.50 M CuNO₃.



d. Ca₃(PO₄)₂ dissolving in a solution of 0.50 M Ca(C₂H₃O₂)₂.



e. Ca₃(PO₄)₂ dissolving in a solution of 0.25 M Na₃PO₄.




 
3. Barium sulfate is an insoluble salt with a K_sp value of 1.1 × 10^-10. Determine its solubility in a 0.50 M solution of Ba(NO₃)₂.



 
 
4. Silver(I) carbonate is an insoluble salt with a K_sp value of 8.1 x 10^-12. Determine its solubility in a 0.50 M solution of AgNO₃.


​